Đố vui. Chu vi Trái Đất bằng bao nhiêu?
Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau:
1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng.
2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-lếch-xăng-đri-a) cách Syene 800 km, Eratosthenes thấy 1 tháp cao 25 m có bóng trên mặt đất dài 3,1 m.
Từ hai quan sát trên, ông có thể tính xấp xỉ “chu vi” của Trái Đất như thế nào? (trên Hình 4.46, điểm O là tâm của Trái Đất, điểm S tượng trưng cho thành phố Syene, điểm A tượng trưng cho thành phố Alexandria, điểm H là đỉnh của tháp, bóng của tháp trên mặt đất được coi là đoạn thẳng AB).
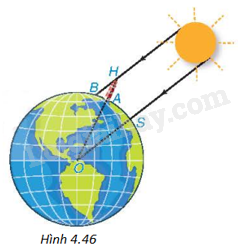
+ Vì đường thẳng vuông góc mặt đất thì đi qua tâm O nên theo giả thiết, tia sáng mặt trời song song với OS, do đó BH song song với OS, suy ra \(\widehat {AHB} = \widehat {AOS}\).
+ Vì \(AH = 25m\) khá bé so với R, Earthostene coi cung tròn AB của (C) là một đoạn thẳng \(AB = 3,1m\) vuông góc với AH tạo thành tam giác BAH vuông tại A, ta có \(\tan \widehat {AHB} = \frac{{AB}}{{AH}}\) nên tính được góc SOA.
+ Vì độ dài cung tròn MN tùy ý trên đường tròn tâm O tỉ lệ thuận với số đo góc ở tâm \(\widehat {MON}\), mà độ dài cung AS bằng 800km ứng với góc ở tâm \(\widehat {AOS} \approx {7^o}\) nên toàn bộ đường tròn (C) ứng với góc ở tâm \({360^o}\) có độ dài xấp xỉ bằng \(\frac{{360}}{7}.800\).
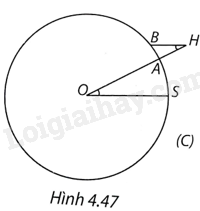
Trên Hình 4.47 đường tròn (C) với O là tâm Trái Đất, đi qua S (Syene), A (Alexandria), \(OS = OA = R\) (R là bán kính của đường tròn (C)).
Theo giả thiết, cung tròn (nhỏ) SA của (C) dài 800km.
Gọi H là đỉnh tháp, chân tại A thì A nằm giữa O và H, \(AH = 25m\). Bóng của tháp là cung tròn AB của (C).
Vì đường thẳng vuông góc mặt đất thì đi qua tâm O nên theo giả thiết, tia sáng mặt trời song song với OS, do đó BH song song với OS, suy ra \(\widehat {AHB} = \widehat {AOS}\).
Vì \(AH = 25m\) khá bé so với R, Earthostene coi cung tròn AB của (C) là một đoạn thẳng \(AB = 3,1m\) vuông góc với AH tạo thành tam giác BAH vuông tại A, ta có \(\tan \widehat {AHB} = \frac{{AB}}{{AH}} = \frac{{3,1}}{{25}} = \frac{{31}}{{250}}\)
Suy ra \(\tan \widehat {AOS} = \frac{{31}}{{250}}\) nên \(\widehat {AOS} \approx {7^o}\)
Vì độ dài cung tròn MN tùy ý trên đường tròn tâm O tỉ lệ thuận với số đo góc ở tâm \(\widehat {MON}\), mà độ dài cung AS bằng 800km ứng với góc ở tâm \(\widehat {AOS} \approx {7^o}\) nên toàn bộ đường tròn (C) ứng với góc ở tâm \({360^o}\) có độ dài xấp xỉ bằng \(\frac{{360}}{7}.800 \approx 41\;143\left( {km} \right)\).

Các bài tập cùng chuyên đề
Bài 1 :
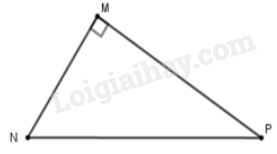
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng
-
A.
$\dfrac{{MN}}{{NP}}$
-
B.
$\dfrac{{MP}}{{NP}}$
-
C.
$\dfrac{{MN}}{{MP}}$
-
D.
$\dfrac{{MP}}{{MN}}$
Bài 2 :
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định đúng.
-
A.
$\sin \alpha + \cos \alpha = 1$
-
B.
${\sin ^2}\alpha + {\cos ^2}\alpha = 1$
-
C.
${\sin ^3}\alpha + {\cos ^3}\alpha = 1$
-
D.
$\sin \alpha - cos\alpha = 1$
Bài 3 :
Cho $\alpha $ là góc nhọn bất kỳ. Chọn khẳng định sai.
-
A.
$\tan \alpha = \dfrac{{\sin \alpha }}{{\cos \alpha }}\,\,$
-
B.
$\cot \alpha = \dfrac{{\cos \alpha }}{{\sin \alpha }}\,\,$
-
C.
$\tan \alpha .\cot \alpha = 1$
-
D.
${\tan ^2}\alpha - 1 = {\cos ^2}\alpha $
Bài 4 :
Cho tam giác $ABC$ vuông tại $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .
-
A.
$\sin B = 0,6;\cos B = 0,8$
-
B.
$\sin B = 0,8;\cos B = 0,6$
-
C.
$\sin B = 0,4;\cos B = 0,8$
-
D.
$\sin B = 0,6;\cos B = 0,4$
Bài 5 :
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
-
A.
$\tan C \approx 0,87$
-
B.
$\tan C \approx 0,86$
-
C.
$\tan C \approx 0,88$
-
D.
$\tan C \approx 0,89$
Bài 6 :
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\cos C \approx 0,76$
-
B.
$\cos C \approx 0,77$
-
C.
$\cos C \approx 0,75$
-
D.
$\cos C \approx 0,78$
Bài 7 :
Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha = \dfrac{2}{5}\).
-
A.
$\sin \alpha = \dfrac{{\sqrt {21} }}{{25}};\cot \alpha = \dfrac{{3\sqrt {21} }}{{21}}$
-
B.
$\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{5}{{\sqrt {21} }}$
-
C.
$\sin \alpha = \dfrac{{\sqrt {21} }}{3};\cot \alpha = \dfrac{3}{{\sqrt {21} }}$
-
D.
$\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{2}{{\sqrt {21} }}$
Bài 8 :
Cho $\alpha $ là góc nhọn bất kỳ. Khi đó $C = {\sin ^4}\alpha + {\cos ^4}\alpha $ bằng
-
A.
$C = 1 - 2{\sin ^2}\alpha .{\cos ^2}\alpha $
-
B.
$C = 1$
-
C.
$C = {\sin ^2}\alpha .{\cos ^2}\alpha $
-
D.
$C = 1 + 2{\sin ^2}\alpha .{\cos ^2}\alpha $
Bài 9 :
Cho $\alpha $ là góc nhọn bất kỳ. Rút gọn $P = \left( {1 - {{\sin }^2}\alpha } \right).{\cot ^2}\alpha + 1 - {\cot ^2}\alpha $ ta được
-
A.
$P = {\sin ^2}\alpha $
-
B.
$P = {\cos ^2}\alpha $
-
C.
$P = {\tan ^2}\alpha $
-
D.
$P = 2{\sin ^2}\alpha $
Bài 10 :
Cho $\alpha $ là góc nhọn bất kỳ. Biểu thức $Q = \dfrac{{1 + {{\sin }^2}\alpha }}{{1 - {{\sin }^2}\alpha }}$ bằng
-
A.
$Q = 1 + {\tan ^2}\alpha $
-
B.
$Q = 1 + 2{\tan ^2}\alpha $
-
C.
$Q = 1 - 2{\tan ^2}\alpha $
-
D.
$Q = 2{\tan ^2}\alpha $
Bài 11 :
Cho $\tan \alpha = 2$. Tính giá trị của biểu thức $G = \dfrac{{2\sin \alpha + \cos \alpha }}{{\cos \alpha - 3\sin \alpha }}$
-
A.
$G =1$
-
B.
$G = - \dfrac{4}{5}$
-
C.
$G = - \dfrac{6}{5}$
-
D.
$G = - 1$
Bài 12 :
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 1:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
-
A.
$2$
-
B.
$3$
-
C.
$1$
-
D.
$4$
Bài 13 :
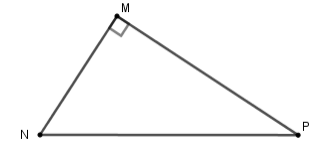
Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
-
A.
\(\dfrac{{MN}}{{NP}}\)
-
B.
\(\dfrac{{MP}}{{NP}}\)
-
C.
\(\dfrac{{MN}}{{MP}}\)
-
D.
\(\dfrac{{MP}}{{MN}}\)
Bài 14 :
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
-
A.
\(\sin B = \dfrac{1}{{\sqrt 3 }};\cos B = \dfrac{{2\sqrt 3 }}{3}\)
-
B.
\(\sin B = \dfrac{{\sqrt 5 }}{5};\cos B = \dfrac{{2\sqrt 5 }}{5}\)
-
C.
\(\sin B = \dfrac{1}{2};\cos B = \dfrac{2}{{\sqrt 5 }}\)
-
D.
\(\sin B = \dfrac{{2\sqrt 5 }}{5};\cos B = \dfrac{{\sqrt 5 }}{5}\)
Bài 15 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 9\,cm,\,\,AC = 5cm.\) Tính tỉ số lượng giác \(\tan C\) (làm tròn đến chữ số thập phân thứ \(1\) )
-
A.
\(\tan C \approx 0,67\)
-
B.
\(\tan C \approx 0,5\)
-
C.
\(\tan C \approx 1,4\)
-
D.
\(\tan C \approx 1,5\)
Bài 16 :
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(CH = 11\,cm,\,BH = 12\,cm.\) Tính tỉ số lượng giác \(\cos C\) (làm tròn đến chữ số thập phân thứ \(2\) )
-
A.
\(\cos C \approx 0,79\)
-
B.
\(\cos C \approx 0,69\)
-
C.
\(\cos C \approx 0,96\)
-
D.
\(\cos C \approx 0,66\)
Bài 17 :
Tính \(\sin \alpha ,\,\,\tan \alpha \) biết \(\cos \alpha = \dfrac{3}{4}\).
-
A.
\(\sin \alpha = \dfrac{4}{{\sqrt 7 }};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\)
-
B.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{3}{{\sqrt 7 }}\)
-
C.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\)
-
D.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{3};\tan \alpha = \dfrac{{\sqrt 7 }}{4}\)
Bài 18 :
Cho \(\alpha \) là góc nhọn bất kỳ. Khi đó \(C={\sin ^6}\alpha + {\cos ^6}\alpha + 3{\sin ^2}\alpha {\cos ^2}\alpha \) bằng
-
A.
\(C = 1 - 3{\sin ^2}\alpha .{\cos ^2}\alpha \)
-
B.
$C=1$
-
C.
\(C = {\sin ^2}\alpha .{\cos ^2}\alpha \)
-
D.
\(C = 3{\sin ^2}\alpha .{\cos ^2}\alpha - 1\)
Bài 19 :
Cho \(\alpha \) là góc nhọn bất kỳ. Cho \(P = \left( {1 - {{\sin }^2}\alpha } \right).{\tan ^2}\alpha + \left( {1 - {{\cos }^2}\alpha } \right){\cot ^2}\alpha \), chọn kết luận đúng.
-
A.
\(P > 1\)
-
B.
\(P < 1\)
-
C.
\(P = 1\)
-
D.
\(P = 2{\sin ^2}\alpha \)
Bài 20 :
Cho \(\alpha \) là góc nhọn bất kỳ. Biểu thức \(Q = \dfrac{{{{\cos }^2}\alpha - {{\sin }^2}\alpha }}{{\cos \alpha .\sin \alpha }}\) bằng
-
A.
\(Q = \cot \alpha - \tan \alpha \)
-
B.
\(Q = \cot \alpha + \tan \alpha \)
-
C.
\(Q = \tan \alpha - \cot \alpha \)
-
D.
\(Q = 2\tan \alpha \)
Bài 21 :
Cho \(\tan \alpha = 4\). Tính giá trị của biểu thức \(P = \dfrac{{3\sin \alpha - 5\cos \alpha }}{{4\cos \alpha + \sin \alpha }}\)
-
A.
\(P = \dfrac{7}{8}\)
-
B.
\(P = \dfrac{{17}}{8}\)
-
C.
\(P = \dfrac{8}{7}\)
-
D.
\(P = \dfrac{5}{8}\)
Bài 22 :
Cho tam giác nhọn \(ABC\) hai đường cao \(AD\) và \(BE\) cắt nhau tại \(H\). Biết \(HD:HA = 3:2\). Khi đó \(\tan \widehat {ABC}.\tan \widehat {ACB}\) bằng
-
A.
$3$
-
B.
$5$
-
C.
\(\dfrac{3}{5}\)
-
D.
\(\dfrac{5}{3}\)
Bài 23 :
Chọn kết luận đúng về giá trị biểu thức \(B = \dfrac{{{{\cos }^2}\alpha - 3{{\sin }^2}\alpha }}{{3 - {{\sin }^2}\alpha }}\) biết \(\tan \alpha = 3.\)
-
A.
\(B > 0\)
-
B.
\(B < 0\)
-
C.
\(0 < B < 1\)
-
D.
\(B = 1\)
Bài 24 :
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
-
A.
\(\sin A = \dfrac{{120}}{{169}}\)
-
B.
\(\sin A = \dfrac{{60}}{{169}}\)
-
C.
\(\sin A = \dfrac{5}{6}\)
-
D.
\(\sin A = \dfrac{{10}}{{13}}\)
Bài 25 :
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{3}{5}\)
-
C.
\(\dfrac{4}{3}\)
-
D.
\(\dfrac{4}{5}\)
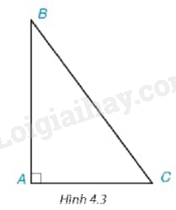
Bài 26 :
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Bài 27 :
Cho tam giác ABC vuông tại A và tam giác A’B’C’ vuông tại A’ có \(\widehat B = \widehat {B'} = \alpha .\) Chứng minh rằng:
a) \(\Delta ABC\backsim \Delta A'B'C';\)
b) \(\frac{{AC}}{{BC}} = \frac{{A'C'}}{{B'C'}};\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}};\frac{{AC}}{{AB}} = \frac{{A'C'}}{{A'B'}};\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Bài 28 :
Cho tam giác ABC vuông tại A có AB = 5 cm, AC = 12 cm. Hãy tính các tỉ số lượng giác của góc B.
Bài 29 :
Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết:
a) AB = 8 cm, BC = 17 cm;
b) AC = 0,9 cm, AB = 1,2 cm.
Bài 30 :
Trong Hình 4.32, \(\cos \alpha \) bằng
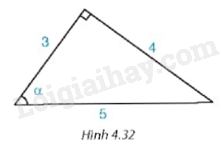
A. \(\frac{5}{3}.\)
B. \(\frac{3}{4}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{4}{5}.\)


















Danh sách bình luận