Đề bài

Một công ty kinh doanh thương mại chuẩn bị cho một đợt khuyến mại nhằm thu hút khách hàng bằn cách tiến hành quảng cáo sản phẩm của công ty trên hệ thống phát thanh và truyền hình. Chi phí cho 1 phút quảng cáo trên sóng phát thanh là 800.000 đồn, trên sóng truyền hình là 4.000.000 đồng. Đài phát thanh chỉ nhận phát các chương trình quảng cáo dài ít nhất là 5 phút. Do nhu cầu quảng cáo trên truyền hình lớn nên đài truyền hình chỉ nhận phát các chươn trình tối đa là 4 phút. Theo các phân tích, cùng thời lượng một phút quảng cáo, trên truyền hình sẽ có hiệu quả gấp 6 lần trên sóng phát thanh. Công ty dự định chi tối đa 16.000.000 dùng cho quảng cáo. Công ty đặt thời lượng quảng cáo trên sóng phát thanh và truyền hình như thế nào để hiệu quả nhất?

Lời giải của GV Loigiaihay.com

Gọi thời lượng công ty đặt quảng cáo trên sóng phát thanh, trên truyền hình lần lượt là x, y (phút) \((x,y \ge 0)\)

Quảng cáo trên phát thanh dài ít nhất 5 phút nên \(x \ge 5\)

Quảng cáo trên truyền hình dài nhiều nhất 4 phút nên \(0 \le y \le 4\)

Hiệu quả chung của quảng cáo là \(F = x + 6y\)

Chi phí cho quảng cáo là: 800 000.x + 4 000 000.y (đồng)

Chi tối đa 16 000 000 đồng cho quảng cáo nên \(800{\rm{ }}000.x{\rm{ }} + {\rm{ }}4{\rm{ }}000{\rm{ }}000.y \le 16\;000\;000\) hay \(x + 5y \le 20\)

Bài toán trở thành: Tìm x,y sao cho \(F = x + 6y\) đạt GTLN  với các điều kiện:

\(\left\{ \begin{array}{l}x \ge 5\\0 \le y \le 4\\x + 5y \le 20\end{array} \right.\) (*)

Biểu diễn miền nghiệm của (*) trên hệ trục Oxy, ta được:

 

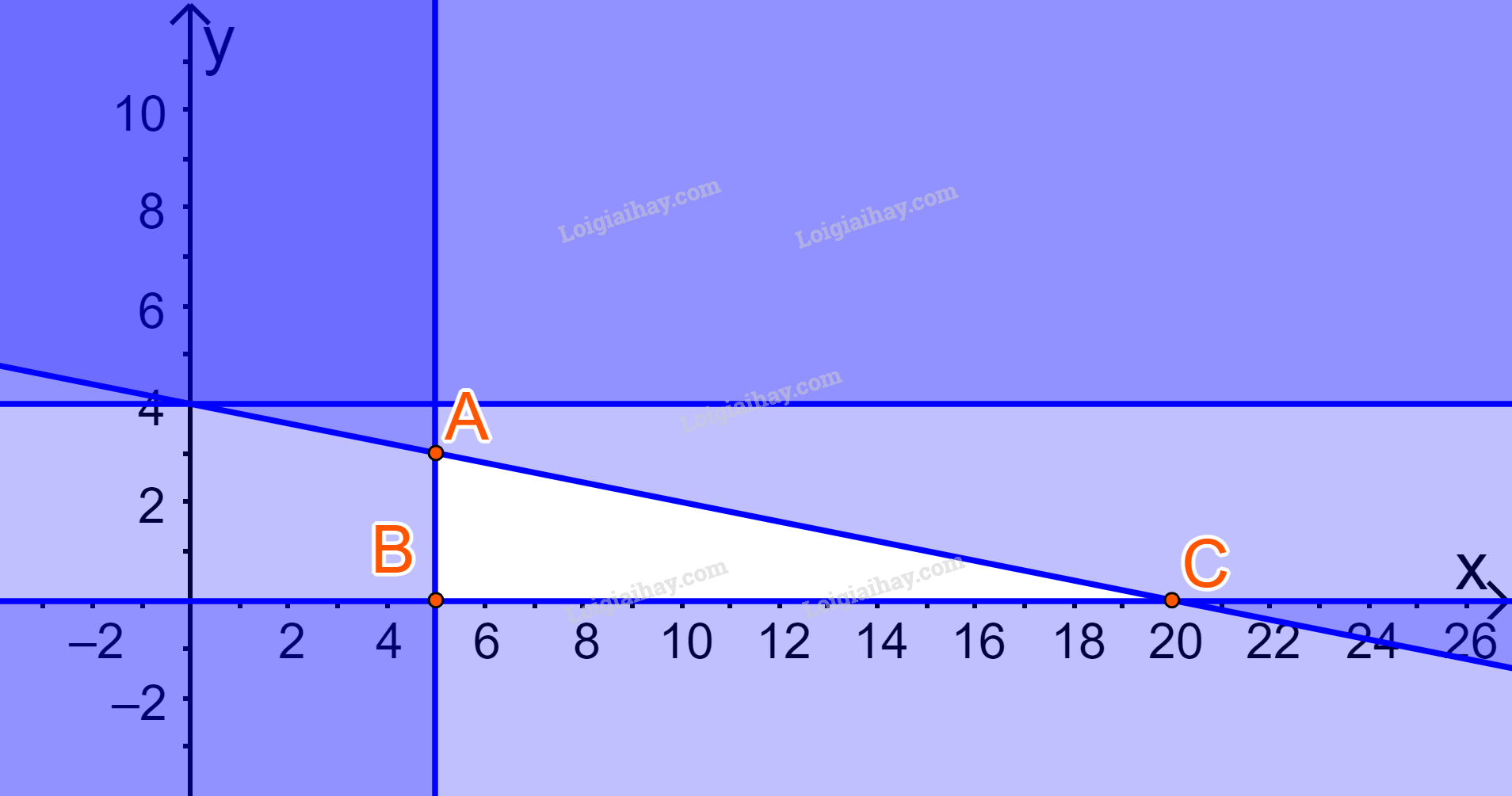
Miền nghiệm là miền tam giác ABC (kể cả các cạnh), trong đó \(A(5;3),B(5;0),C(20;0)\)

Lần lượt thay tọa độ các điểm A, B, C, D vào biểu thức \(F(x;y) = x + 6y\) ta được:

\(\begin{array}{l}F(5;3) = 5 + 6.3 = 23\\F(5;0) = 5 + 6.0 = 5\\F(20;0) = 20 + 6.0 = 20\end{array}\)

Do đó F đạt giá trị lớn nhất bằng 23 tại \(x = 5;y = 3\)

Vậy công ty đó nên đặt quảng cáo 5 phút trên sóng phát thanh và 3 phút trên truyền hình để đạt hiệu quả cao nhất.