Trong không gian Oxyz, cho vecto \(\overrightarrow a = (2;1; - 2)\), \(\overrightarrow b = (0; - 1;1)\).
a) \(\left| {\overrightarrow a } \right| = 3\)
b) \(\overrightarrow a + \overrightarrow b = (2;0; - 1)\)
c) \(\overrightarrow a .\overrightarrow b = - 1\)
d) Góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng \({60^o}\)
a) \(\left| {\overrightarrow a } \right| = 3\)
b) \(\overrightarrow a + \overrightarrow b = (2;0; - 1)\)
c) \(\overrightarrow a .\overrightarrow b = - 1\)
d) Góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng \({60^o}\)
Sử dụng các quy tắc cộng vecto, công thức tính tích vô hướng của hai vecto, độ dài vecto, góc giữa hai vecto.
a) Đúng. Vì \(\left| {\overrightarrow a } \right| = \sqrt {{2^2} + {1^2} + {{( - 2)}^2}} = 3\).
b) Đúng. Vì \(\overrightarrow a + \overrightarrow b = (2 + 0;1 - 1; - 2 + 1) = (2;0; - 1)\).
c) Sai. Vì \(\overrightarrow a .\overrightarrow b = 2.0 + 1.( - 1) - 2.1 = - 3\).
d) Sai. Vì \[\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{ - 3}}{{\sqrt {{2^2} + {1^2} + {{( - 2)}^2}} .\sqrt {{0^2} + {{( - 1)}^2} + {1^2}} }} = \frac{{ - \sqrt 2 }}{2}\] nên góc giữa hai vecto \(\overrightarrow a ,\overrightarrow b \) bằng \({135^o}\).
Các bài tập cùng chuyên đề
Trong Ví dụ 3, tính \({\left( {\overrightarrow a + \overrightarrow b } \right)^2}\).
Trong không gian Oxyz, cho hai vectơ \(\overrightarrow a = \left( { - 2;1;2} \right),\overrightarrow b = \left( {1;1; - 1} \right)\).
a) Xác định tọa độ của vectơ \(\overrightarrow u = \overrightarrow a - 2\overrightarrow b \).
b) Tính độ dài vectơ \(\overrightarrow u \).
c) Tính \(\cos \left( {\overrightarrow a ;\overrightarrow b } \right)\).
Trong không gian Oxyz, cho các điểm \(A\left( {2; - 1;3} \right),B\left( {1;1; - 1} \right)\) và \(C\left( { - 1;0;2} \right)\).
a) Tìm tọa độ trọng tâm G của tam giác ABC.
b) Tìm tọa độ điểm M thuộc trục Oz sao cho đường thẳng BM vuông góc với đường thẳng AC.
Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a = \left( {3;1;2} \right)\), \(\overrightarrow b = \left( { - 3;0;4} \right)\) và \(\overrightarrow c = \left( {6; - 1;0} \right)\)
a) Tìm tọa độ của các vectơ \(\overrightarrow a + \overrightarrow b + \overrightarrow c \) và \(2\overrightarrow a - 3\overrightarrow b - 5\overrightarrow c \).
b) Tính các tích vô hướng \(\overrightarrow a .\left( { - \overrightarrow b } \right)\) và \(\left( {2\overrightarrow a } \right).\overrightarrow c \).
Trong không gian Oxyz, cho ba vectơ \(\overrightarrow a = \left( {3;1;2} \right)\), \(\overrightarrow b = \left( { - 3;0;4} \right)\) và \(\overrightarrow c = \left( {6; - 1;0} \right)\)
a) Tìm tọa độ của các vectơ \(\overrightarrow a + \overrightarrow b + \overrightarrow c \) và \(2\overrightarrow a - 3\overrightarrow b - 5\overrightarrow c \).
b) Tính các tích vô hướng \(\overrightarrow a .\left( { - \overrightarrow b } \right)\) và \(\left( {2\overrightarrow a } \right).\overrightarrow c \).
Trong không gian Oxyz, cho ba điểm \(M\left( { - 4;3;3} \right),N\left( {4; - 4;2} \right)\) và \(P\left( {3;6; - 1} \right)\).
a) Tìm tọa độ của các vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} \), từ đó chứng minh rằng ba điểm M, N, P không thẳng hàng.
b) Tìm tọa độ của vectơ \(\overrightarrow {NM} + \overrightarrow {NP} \), từ đó suy ra tọa độ của điểm Q sao cho tứ giác MNPQ là hình bình hành.
c) Tính chu vi của hình bình hành MNPQ.
Trong không gian Oxyz, cho tam giác ABC có \(A\left( {1;0;1} \right),B\left( {0; - 3;1} \right)\) và \(C\left( {4; - 1;4} \right)\).
a) Tìm tọa độ trọng tâm của tam giác ABC.
b) Chứng minh rằng \(\widehat {BAC} = {90^0}\).
c) Tính \(\widehat {ABC}\).
Trong không gian với hệ tọa độ Oxyz, cho A(-2;3;0), B(4;0;5), C(0;2;-3).
a) Chứng minh rằng ba điểm A, B, C không thẳng hàng
b) Tính chu vi tam giác ABC
c) Tìm tọa độ trọng tâm G của tam giác ABC
d) Tính \(\cos \widehat {BAC}\)
Trong không gian với hệ tọa độ Oxyz, cho A(2;0;-3), B(0;-4;5) và C(-1;2;0).
a) Chứng minh rằng ba điểm A, B, C không thằng hàng
b) Tìm tọa độ của điểm D sao cho tứ giác ABCD là hình bình hành
c) Tìm tọa độ trọng tâm G của tam giác ABC
d) Tính chu vi của tam giác ABC
e) Tính \(\cos \widehat {BAC} \)
Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {5;7; - 4} \right),B\left( {6;8; - 3} \right),C\left( {6;7; - 3} \right),D'\left( {3;0;3} \right)\). Tìm toạ độ các đỉnh \(D\) và \(A'\).
Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {2;0;2} \right),B\left( {4;2;4} \right),D\left( {2; - 2;2} \right),C'\left( {8;10; - 10} \right)\). Tìm toạ độ điểm \(A'\).
Cho hình bình hành \(OABD\) có \(\overrightarrow {OA} = \left( { - 1;1;0} \right)\) và \(\overrightarrow {OB} = \left( {1;1;0} \right)\) với \(O\) là gốc toạ độ. Tìm toạ độ của điểm \(D\).
Cho tứ diện \(OABC\) có \(G\left( {3; - 3;6} \right)\) là trọng tâm. Tìm toạ độ điểm \(A\) thoả mãn \(\overrightarrow {AB} = \left( {1;2;3} \right)\) và \(\overrightarrow {AC} = \left( { - 1;4; - 2} \right)\).
Cho hình hộp \(ABCD.A'B'C'D'\) có \(A\left( {2;4;0} \right),B\left( {4;0;0} \right),C\left( { - 1;4; - 7} \right)\) và \(D'\left( {6;8;10} \right)\). Tìm toạ độ của điểm \(B'\).
Cho điểm \(A\left( {2;2;1} \right)\). Tính độ dài đoạn thẳng \(OA\).
Cho điểm \(A\left( {1;2;3} \right)\). Tính khoảng cách từ \(A\) đến trục \(Oy\).
Cho điểm \(M\left( {3; - 1;2} \right)\). Tìm:
a) Toạ độ điểm \(M'\) là điểm đối xứng của điểm \(M\) qua gốc toạ độ \(O\).
b) Toạ độ điểm \(O'\) là điểm đối xứng của điểm \(O\) qua điểm \(M\).
c) Khoảng cách từ \(M\) đến gốc toạ độ.
d) Khoảng cách từ \(M\) đến mặt phẳng \(\left( {Oxz} \right)\).
Cho điểm \(M\left( {a;b;c} \right)\). Gọi \(A,B,C\) theo thứ tự là điểm đối xứng của điểm \(M\) qua các mặt phẳng \(\left( {Oxy} \right),\left( {Oyz} \right),\left( {Oxz} \right)\). Tìm toạ độ trọng tâm của tam giác \(ABC\).
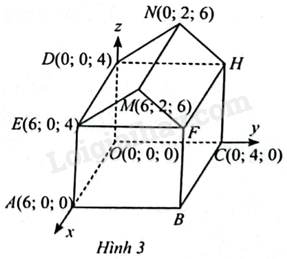
Một nhân viên đang sử dụng phần mềm để thiết kế khung của một ngôi nhà trong không gian \(Oxyz\) được minh hoạ như Hình 3. Cho biết \(OABC.DEFH\) là hình hộp chữ nhật và \(EMF.DNH\) là hình lăng trụ đứng.
a) Tìm toạ độ của các điểm \(B,F,H\).
b) Tìm toạ độ của các vectơ \(\overrightarrow {ME} ,\overrightarrow {MF} \).
c) Tính số đo \(\widehat {EMF}\).
Cho hai điểm \(A\left( {2;0;1} \right)\) và \(B\left( {0;5; - 1} \right)\). Tích vô hướng của hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) bằng
A. ‒2.
B. ‒1.
C. 1.
D. 2.
Cho ba vectơ \(\overrightarrow a = \left( { - 1;1;0} \right),\overrightarrow b = \left( {1;1;0} \right)\) và \(\overrightarrow c = \left( {1;1;1} \right)\). Trong các khẳng định sau, khẳng định nào sai?
A. \(\left| {\overrightarrow a } \right| = \sqrt 2 \).
B. \(\left| {\overrightarrow c } \right| = \sqrt 3 \).
C. \(\overrightarrow a \bot \overrightarrow b \).
D. \(\overrightarrow c \bot \overrightarrow b \).
Cho hai vectơ \(\overrightarrow a = \left( { - 3;4;0} \right)\) và \(\overrightarrow b = \left( {5;0;12} \right)\). Côsin của góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) bằng
A. \(\frac{3}{{13}}\).
B. \(\frac{5}{6}\).
C. \( - \frac{5}{6}\).
D. \( - \frac{3}{{13}}\).
Góc giữa hai vectơ \(\overrightarrow i \) và \(\overrightarrow u = \left( { - \sqrt 3 ;0;1} \right)\) bằng
A. \({30^ \circ }\).
B. \({60^ \circ }\).
C. \({120^ \circ }\).
D. \({150^ \circ }\).
Hai vectơ \(\overrightarrow a = \left( {m;2;3} \right)\) và \(\overrightarrow b = \left( {1;n;2} \right)\) cùng phương khi
A. \(\left\{ \begin{array}{l}m = \frac{1}{2}\\n = \frac{4}{3}\end{array} \right.\).
B. \(\left\{ \begin{array}{l}m = \frac{3}{2}\\n = \frac{4}{3}\end{array} \right.\).
C. \(\left\{ \begin{array}{l}m = \frac{3}{2}\\n = \frac{2}{3}\end{array} \right.\).
D. \(\left\{ \begin{array}{l}m = \frac{2}{3}\\n = \frac{4}{3}\end{array} \right.\).
Cho hai điểm \(A\left( {2;3; - 1} \right)\) và \(B\left( {0; - 1;1} \right)\). Trung điểm \(I\) của đoạn thẳng \(AB\) có toạ độ là
A. \(\left( {1;1;0} \right)\).
B. \(\left( {2;2;0} \right)\).
C. \(\left( { - 2; - 4;2} \right)\).
D. \(\left( { - 1; - 2;1} \right)\).
Cho hai vectơ \(\overrightarrow a = \left( {1;1; - 2} \right),\overrightarrow b = \left( { - 3;0; - 1} \right)\) và điểm \(A\left( {0;2;1} \right)\). Toạ độ điểm \(M\) thoả mãn \(\overrightarrow {AM} = 2\overrightarrow a - \overrightarrow b \) là
A. \(M\left( { - 5;1;2} \right)\).
B. \(M\left( {3; - 2;1} \right)\).
C. \(M\left( {1;4; - 2} \right)\).
D. \(M\left( {5;4; - 2} \right)\).
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng 2.
a) \(\overrightarrow {AB} = \overrightarrow {C'D'} \).
b) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {D'C'} \).
c) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
d) \(\overrightarrow {AC} .\overrightarrow {AD'} = 8\).
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
Cho hai điểm \(A\left( {3; - 2;4} \right),B\left( {5;0;7} \right)\).
a) \(\overrightarrow {OA} = 3\overrightarrow i - 2\overrightarrow j + 4\overrightarrow k \).
b) \(\overrightarrow {AB} = \left( {8; - 2;11} \right)\).
c) Điểm \(B\) nằm trong mặt phẳng \(\left( {Oxz} \right)\).
d) \(2\overrightarrow {OB} = \left( {10;0;14} \right)\).
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.
Cho hai vectơ \(\overrightarrow a = \left( {2;1;5} \right)\) và \(\overrightarrow b = \left( {5;0; - 2} \right)\)
a) \(\left| {\overrightarrow a } \right| = \sqrt {30} \).
b) \(\overrightarrow a ,\overrightarrow b \)cùng phương.
c) \(\overrightarrow a + \overrightarrow b = \left( {7;1;3} \right)\).
d) \(\overrightarrow a .\overrightarrow b = 1\).
Chọn đúng hoặc sai cho mỗi ý a, b, c, d
Cho một lực \(\overrightarrow F = \left( {4;6;9} \right)\) (đơn vị: \(N\)) thực hiện một độ dịch chuyển \(\overrightarrow d = \left( {20;50;10} \right)\) (đơn vị: m).
a) Cường độ của lực \(\overrightarrow F \) là \(\sqrt {133} N\).
b) Độ dài quãng đường dịch chuyển là \(10\sqrt {30} m\).
c) Công sinh bởi lực \(\overrightarrow F \) khi thực hiện độ dời \(\overrightarrow d \) là \(10\sqrt {3990} J\).
d) \(\cos \left( {\overrightarrow F ,\overrightarrow d } \right) = \frac{{470}}{{10\sqrt {3990} }}\).
