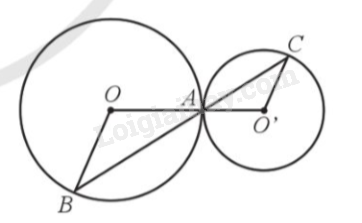
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài với nhau tại A, hai điểm \(B \in \left( O \right)\) và \(C \in \left( {O'} \right)\) sao cho B và C nằm cùng phía đối với đường thẳng OO’ và OB//O’C.
a) Chứng minh góc BAC là góc vuông.
b) Cho biết \(R = 3cm\), \(R' = 1cm\) và BC cắt OO’ tại D. Tính độ dài đoạn OD.
a) + Chứng minh tam giác AOB cân tại O nên \(\widehat {{A_1}} = \widehat {{B_1}}\).
+ Tam giác AOB có:
\(\widehat {{A_1}} + \widehat {{O_1}} + \widehat {{B_1}} = 2\widehat {{A_1}} + \widehat {{O_1}} = {180^o}\) nên \(2\widehat {{A_1}} = {180^o} - \widehat {{O_1}}\).
+ Chứng minh tam giác AO’C cân tại O’. Do đó, \(\widehat {{A_2}} = \widehat {O'CA}\).
+ Tam giác AO’C có:
\(\widehat {{A_2}} + \widehat {O{'_1}} + \widehat {O'CA} = 2\widehat {{A_2}} + \widehat {O{'_1}} = {180^o}\) nên \(2\widehat {{A_2}} = {180^o} - \widehat {O{'_1}}\).
+ Do đó:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - \left( {\widehat {{O_1}} + \widehat {O{'_1}}} \right)\) (1)
Chứng minh
\(\widehat {{O_2}} = \widehat {O{'_1}}\), \(\widehat {{O_2}} + \widehat {{O_1}} = {180^o}\) nên \(\widehat {{O_1}} + \widehat {O{'_1}} = {180^o}\) (2)
Từ (1) và (2) ta có:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - {180^o} = {180^o}\) nên \(\widehat {BAC} = {90^o}\).
b) + Ta có: \(OA = OB = R = 3cm,O'A = O'C = R' = 1cm\).
+ Chứng minh \(\frac{{DO}}{{DO'}} = \frac{{OB}}{{O'C}} = \frac{3}{1}\)
+ \(DO' = DO - OO' = DO - \left( {OA + O'A} \right)\) \( = DO - \left( {3 + 1} \right) = DO - 4\) (4)
+ Do đó, \(\frac{{DO}}{{DO - 4}} = \frac{3}{1}\), từ đó tính được DO.
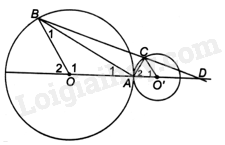
a) Vì \(OA = OB\) (bán kính của (O)) nên tam giác AOB cân tại O. Do đó, \(\widehat {{A_1}} = \widehat {{B_1}}\).
Tam giác AOB có:
\(\widehat {{A_1}} + \widehat {{O_1}} + \widehat {{B_1}} = 2\widehat {{A_1}} + \widehat {{O_1}} = {180^o}\) nên \(2\widehat {{A_1}} = {180^o} - \widehat {{O_1}}\).
Vì \(O'A = O'C\) (bán kính của (O’)) nên tam giác AO’C cân tại O’. Do đó, \(\widehat {{A_2}} = \widehat {O'CA}\).
Tam giác AO’C có:
\(\widehat {{A_2}} + \widehat {O{'_1}} + \widehat {O'CA} = 2\widehat {{A_2}} + \widehat {O{'_1}} = {180^o}\) nên \(2\widehat {{A_2}} = {180^o} - \widehat {O{'_1}}\).
Do đó:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - \left( {\widehat {{O_1}} + \widehat {O{'_1}}} \right)\) (1)
Vì OB//O’C nên \(\widehat {{O_2}} = \widehat {O{'_1}}\) (hai góc đồng vị).
Lại có: \(\widehat {{O_2}} + \widehat {{O_1}} = {180^o}\) nên \(\widehat {{O_1}} + \widehat {O{'_1}} = {180^o}\) (2).
Từ (1) và (2) ta có:
\(2\left( {\widehat {{A_1}} + \widehat {{A_2}}} \right) = {360^o} - {180^o} = {180^o}\) nên \(\widehat {{A_1}} + \widehat {{A_2}} = {90^o}\), suy ra \(\widehat {BAC} = {90^o}\).
b) Ta có: \(OA = OB = R = 3cm,O'A = O'C = R' = 1cm\).
Tam giác DOB có O’C//OB nên
\(\frac{{DO}}{{DO'}} = \frac{{OB}}{{O'C}} = \frac{3}{1}\) (3)
Lại có:
\(DO' = DO - OO' = DO - \left( {OA + O'A} \right) \\= DO - \left( {3 + 1} \right) = DO - 4 \;(4)\)
Từ (3) và (4) ta có:
\(\frac{{DO}}{{DO - 4}} = \frac{3}{1}\), suy ra \(DO = 3\left( {DO - 4} \right)\), hay \(2DO = 12\), suy ra \(DO = 6cm\).

Các bài tập cùng chuyên đề
Bài 1 :
Nếu hai đường tròn tiếp xúc với nhau thì số điểm chung của hai đường tròn là
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Bài 2 :
Cho đường tròn $\left( O \right)$ bán kính $OA$ và đường tròn $\left( {O'} \right)$ đường kính $OA$.
Bài 3 :
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ các đường kính $AOB;AO'C$. Gọi $DE$ là tiếp tuyến chung của hai đường tròn $\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)$. Gọi $M$ là giao điểm của $BD$ và $CE$. Tính diện tích tứ giác $ADME$ biết $\widehat {DOA} = 60^\circ $ và $OA = 6\,cm.$
-
A.
$12\sqrt 3 \,\,c{m^2}$
-
B.
$12\,\,c{m^2}$
-
C.
$16\,\,c{m^2}$
-
D.
$24\,\,c{m^2}$
Bài 4 :
Cho hai đường tròn $\left( O \right)$ và $\left( {O'} \right)$ tiếp xúc ngoài tại $A$. Kẻ tiếp tuyến chung ngoài $BC,B \in \left( O \right)$ và $C \in (O')$. Tiếp tuyến chung trong tại $A$ cắt tiếp tuyến chung ngoài $BC$ tại $I$. Tính độ dài $BC$ biết $OA = 9cm,O'A = 4cm$.
-
A.
$12cm$
-
B.
$18cm$
-
C.
$10cm$
-
D.
$6cm$
Bài 5 :
Nếu hai đường tròn không cắt nhau thì số điểm chung của hai đường tròn là
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(0\)
Bài 6 :
Cho đoạn \(OO'\) và điểm \(A\) nằm trên đoạn \(OO'\) sao cho \(OA = 2O'A.\) Đường tròn \(\left( O \right)\) bán kính \(OA\) và đường tròn \(\left( {O'} \right)\) bán kính \(O'A\).
Bài 7 :
Cho hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\)tiếp xúc ngoài tại \(A\). Kẻ các đường kính \(AOB;AO'C\). Gọi \(DE\) là tiếp tuyến chung của hai đường tròn \(\left( {D \in \left( O \right);E \in \left( {O'} \right)} \right)\). Gọi \(M\) là giao điểm của \(BD\) và \(CE\). Tính diện tích tứ giác \(ADME\) biết \(\widehat {DOA} = 60^\circ \) và \(OA = 8\,cm\)
-
A.
\(12\sqrt 3 \,\,c{m^2}\)
-
B.
\( \dfrac{64}{3}\sqrt 3 \,\,c{m^2}\)
-
C.
\( \dfrac{32}{3}\sqrt 3 \,\,c{m^2}\)
-
D.
\(36\,\,c{m^2}\)
Bài 8 :
Cho các đường tròn \(\left( {A;10\,{\rm{cm}}} \right),{\rm{ }}\left( {B;15\,{\rm{cm}}} \right),{\rm{ }}\left( {C;15\,cm} \right)\) tiếp xúc ngoài với nhau đôi một. Hai đường tròn (B) và (C) tiếp xúc với nhau tại \(A'\). Đường tròn \(\left( A \right)\) tiếp xúc với đường tròn \(\left( B \right)\) và \(\left( C \right)\) lần lượt tại \(C'\) và \(B'.\)
Bài 9 :
Cho hai đường tròn \(\left( {I;7cm} \right)\) và \(\left( {K;5cm} \right)\). Biết \(IK = 2cm\). Quan hệ giữa hai đường tròn là:
-
A.
Tiếp xúc trong
-
B.
Tiếp xúc ngoài
-
C.
Cắt nhau
-
D.
Đựng nhau
Bài 10 :
Hai đường tròn \(\left( {O;5} \right)\) và \(\left( {O';8} \right)\) có vị trí tương đối với nhau như thế nào biết \(OO' = 12\)
-
A.
Tiếp xúc nhau
-
B.
Không giao nhau
-
C.
Tiếp xúc ngoài
-
D.
Cắt nhau
Bài 11 :
Cho hai đường tròn \(\left( {O;4cm} \right)\)và \(\left( {I;6cm} \right)\). Biết \(OI = 2cm\). Tìm vị trí tương đối của hai đường tròn.
-
A.
Tiếp xúc ngoài
-
B.
Đựng nhau
-
C.
Tiếp xúc trong
-
D.
Cắt nhau.
Bài 12 :
Trên hình 5.33a, ta có OO’ = OA + O’A; trên Hình 5.33b, ta có OO’ = OA. Trong mỗi trường hợp, hãy vẽ hai đường tròn (O; OA) và (O; O’A) và cho biết hai đường tròn đó có mấy điểm chung?

Bài 13 :
Cho ba điểm thẳng hàng O, A và O’. Với mỗi trường hợp sau, hãy viết hệ thức giữa các độ dài OO’, OA và O’A rồi xét xem hai đường tròn (O; OA) và (O’; O’A) tiếp xúc trong hay tiếp xúc ngoài với nhau; vẽ hình để khẳng định dự đoán của mình.
a) Điểm A nằm giữa hai điểm O và O’;
b) Điểm O nằm giữa hai điểm A và O’;
c) Điểm O’ nằm giữa hai điểm A và O.
Bài 14 :
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng minh rằng OB // O’C.
Bài 15 :
Hình 12 mô tả các ống tròn xếp lên nhau và gợi nên hình ảnh các cặp đường tròn tiếp xúc nhau. Theo em, hai đường tròn tiếp xúc nhau thì chúng có bao nhiêu điểm chung?

Bài 16 :
Trong Hình 5.21, hai đường tròn (A; 3) và (B; 4) tiếp xúc ngoài nhau. Sử dụng compa và thước thẳng để dựng đường tròn (C; 2) tiếp xúc ngoài với cả hai đường tròn (A) và (B).
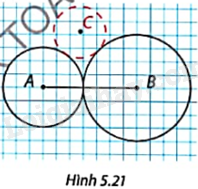
Bài 17 :
Sử dụng compa và thước đo độ dài, hãy vẽ hai đường tròn bán kính lần lượt 5cm và 4cm tiếp xúc nhau.
Bài 18 :
Xác định vị trí tương đối của hai đường tròn có đường kính lần lượt là 8cm và 12cm, biết khoảng cách giữa hai tâm của hai đường tròn là 10cm.
Bài 19 :
Ba đường tròn (A; 2), (B; 10) và (C; 3) đôi một tiếp xúc ngoài nhau như trong Hình 5.23. Chứng minh rằng \(\Delta ABC\) là tam giác vuông.
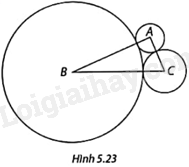
Bài 20 :
Hai đường tròn có bán kính lần lượt là 7cm và 8cm. Khoảng cách giữa các tâm của hai đường tròn là 15cm. Vị trí tương đối của hai đường tròn là
A. Cắt nhau.
B. Tiếp xúc trong.
C. Tiếp xúc ngoài.
D. Ngoài nhau.
Bài 21 :
Cho hai đường tròn (O; 2,5 cm) và (O'; 4,5 cm). Tìm độ dài đoạn thẳng OO' biết hai đường tròn đó tiếp xúc trong.
Bài 22 :
Cho I là trung điểm của đoạn AB. Xét các đường tròn (I; IB) và (A; AB).
a) Hai đường tròn (I) và (A) nói trên có vị trí tương đối như thế nào?
b) Đường thẳng đi qua B, cắt các đường tròn (I) và (A) lần lượt tại C và D. Hãy so sánh các độ dài BC và CD.
Bài 23 :
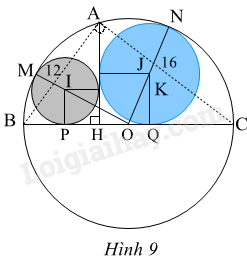
Trong Hình 9, cho biết AB = 12, AC = 16; đường tròn (I) tiếp xúc với AH, BC và đường tròn (O); đường tròn (J) tiếp xúc với AH, BC và đường tròn (O). Tính:
a) BC, BH.
b) Bán kính R, R’ của đường tròn (I) và (J).
c) Khoảng cách PQ.
Bài 24 :
Cho hai đường tròn (O; 3,5 cm) và (O'; 4,5 cm). Tìm độ dài OO’ sao cho hai đường tròn đó tiếp xúc ngoài.
Bài 25 :
Cho đường tròn tâm O bán kính OA và đường tròn tâm O' đường kính OA.
a) Xét vị trí tương đối của hai đường tròn (O) và (O').
b) Dây AD của đường tròn (O) cắt đường tròn (O’) tại C. Chứng minh AC = CD.
Bài 26 :
Cho đường tròn (O; 3 cm) và (O'; 2 cm) tiếp xúc ngoài với nhau tại A. Một đường thẳng đi qua A cắt (O) và (O') lần lượt tại B và C (B và C khác A).
Bài 27 :
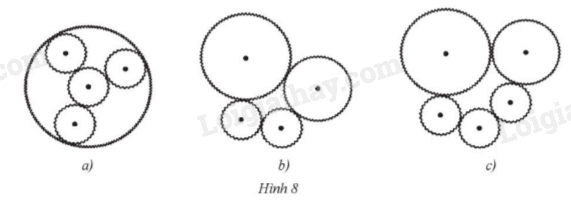
Trong mỗi hình 8a, 8h, 8c, các bánh xe tròn có răng cưa được khớp với nhau. Hình nào có hệ thống bánh răng chuyển động được? Hình nào có hệ thống bánh răng không chuyển động được?
Bài 28 :
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài với nhau tại A. Một đường thẳng qua A cắt (O) tại B và cắt (O’) tại C. Chứng mỉnh rằng OB//O’C.
Bài 29 :
Cho hai đường tròn \((O,11cm)\) và \((O',1cm)\), biết \(OO' = 5cm\). Vị trí tương đối của hai đường tròn là
-
A.
Tiếp xúc trong.
-
B.
Ở ngoài nhau.
-
C.
Tiếp xúc ngoài.
-
D.
Đường tròn \((O)\) đựng \((O')\).
Bài 30 :
Cho đường tròn (O) đường kính 8cm và đường tròn \((O';2cm)\). OA là một bán kính của (O) (A \( \in \) (O)) và \(O'\) là trung điểm của đoạn \(OA\). Vị trí tương đối của hai đường tròn trên là
-
A.
Tiếp xúc ngoài.
-
B.
Cắt nhau.
-
C.
Ở ngoài nhau.
-
D.
Tiếp xúc trong.


















Danh sách bình luận