Cho hình thang cân ABCD (AB//CD).
a) Chứng minh rằng đường trung trực d của AB cũng là đường trung trực của CD (từ đó suy ra hai điểm A và B đối xứng với nhau, C và D đối xứng với nhau qua d).
b) Giải thích tại sao nếu một đường tròn đi qua ba điểm A, B và C thì nó cũng đi qua điểm D.
a) - Trường hợp 1: DA cắt CB tại điểm S.
+ Chứng minh tam giác SAB cân tại S và tam giác SDC cân tại S.
+ Do đó, đường trung trực d của AB là đường phân giác của góc ASB và cũng là đường trung trực của DC. Suy ra, A và D lần lượt đối xứng với B và C qua d.
- Trường hợp 2: DA//CB. Khi đó hình thang cân ABCD là hình chữ nhật. Do đó, A và D lần lượt đối xứng với B và C qua d.
b) + Giả sử O là tâm của đường tròn đi qua ba điểm A, B, C.
+ Chứng minh đường trung trực d của AB đi qua O, suy ra d là trục đối xứng của đường tròn (O).
+ Vì D đối xứng với C qua d, mà \(C \in \left( O \right)\) nên \(D \in \left( O \right)\), hay (O) đi qua D.
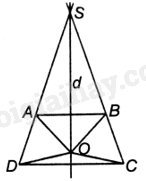
a) Trường hợp 1: DA cắt CB tại điểm S.
Vì ABCD là hình thang cân nên \(\widehat {SAB} = \widehat {SBA} = \widehat {SDC} = \widehat {SCD}\), suy ra tam giác SAB cân tại S và tam giác SDC cân tại S.
Do đó, đường trung trực d của AB là đường phân giác của góc ASB và cũng là đường trung trực của DC.
Suy ra, A và D lần lượt đối xứng với B và C qua d.
Trường hợp 2: DA//CB.
Khi đó hình thang cân ABCD là hình chữ nhật.
Do đó, A và D lần lượt đối xứng với B và C qua d.
b) Giả sử O là tâm của đường tròn đi qua ba điểm A, B, C.
Khi đó, đường trung trực d của AB đi qua O (vì \(OA = OB\)).
Do đó, d là trục đối xứng của đường tròn (O).
Theo câu a, D đối xứng với C qua d, mà \(C \in \left( O \right)\) nên \(D \in \left( O \right)\), hay (O) đi qua D.

Các bài tập cùng chuyên đề
Bài 1 :
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
-
A.
Đường tròn không có trục đối xứng
-
B.
Đường tròn có duy nhất một trục đối xứng là đường kính
-
C.
Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau
-
D.
Đường tròn có vô số trục đối xứng là đường kính.
Bài 2 :
Đường tròn là hình:
-
A.
Không có trục đối xứng
-
B.
Có một trục đối xứng
-
C.
Có hai trục đối xứng
-
D.
Có vô số trục đối xứng
Bài 3 :
Điền từ thích hợp vào chỗ trống: “Đường tròn có… trục đối xứng.”
-
A.
$1$
-
B.
$2$
-
C.
vô số
-
D.
$3$
Bài 4 :
Cho đường tròn tâm O và hai điểm A, B thuộc (O). Gọi d là đường trung trực của đoạn AB. Chứng minh rằng d là một trục đối xứng của (O).
Bài 5 :
Cho dây AB không qua tâm của đường tròn (O). Gọi A’ và B’ là hai điểm lần lượt đối xứng với A và B qua (O). Hỏi đường trung trực của A’B’ có phải là trục đối xứng của (O) hay không? Tại sao?
Bài 6 :
Nêu cách chia một cái bánh có dạng hình tròn tâm O (Hình 8) thành hai phần bằng nhau.

Bài 7 :
Bạn Hoa có một tờ giấy hình tròn. Nêu cách gấp giấy để xác định tâm đường tròn đó.
Bài 8 :
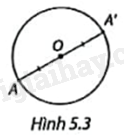
Lấy điểm A bất kì trên đường tròn và xác định điểm A’ sao cho O là trung điểm của đoạn thẳng AA’ (Hình 5.3). Điểm A’ có nằm trên đường tròn không? Vì sao?
Bài 9 :
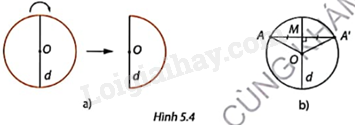
1. Cắt một hình tròn có tâm O bằng giấy và kẻ một đường kính d bất kì. Gấp đôi hình tròn theo đường kính vừa vẽ (Hình 5.4a). Hai nửa đường tròn có chồng khít lên nhau không?
2. Lấy điểm A bất kì trên đường tròn và xác định điểm A’ sao cho đường kính d là đường trung trực của đoạn thẳng AA’. So sánh OA và OA’ và cho biết điểm A’ có nằm trên đường tròn không?
Bài 10 :
Vẽ đường tròn (O) và vẽ bốn trục đối xứng khác nhau của (O). Đường tròn (O) có bao nhiêu trục đối xứng?
Bài 11 :
Cho đường tròn (O) đường kính AB, vẽ dây CD vuông góc với AB tại M. Cho biết AM = 1 cm, CD = \(2\sqrt 3 \) cm. Tính
a) Bán kính đường tròn (O).
b) Số đo \(\widehat {CAB}\).
Bài 12 :
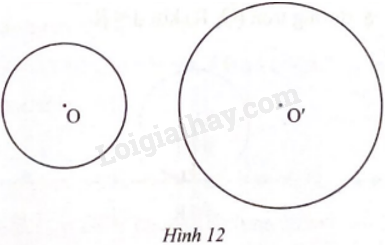
Tìm trục đối xứng của hình tạo bởi hai đường tròn (O) và (O’) trong Hình 12.
Bài 13 :
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn?
A. Đường tròn không có trục đối xứng.
B. Đường tròn có duy nhất một trục đối xứng là đường kính.
C. Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau.
D. Đường tròn có vô số trục đối xứng là đường kính.
Bài 14 :
Cho dây AB không đi qua tâm của đường tròn (O). Gọi A’ và B’ là hai điểm lần lượt đối xứng với A và B qua O. Hỏi đường trung trực của A’B’ có phải là trục đối xứng của (O) hay không? Tại sao?


















Danh sách bình luận