Chọn câu sai:
Cho góc nhọn \(\alpha \) có \(\sin \alpha = \frac{1}{2}\) thì
A. \(\frac{1}{{\tan \alpha }} = \sqrt 3 \).
B. \(\frac{1}{{\sin \alpha }} = 2\).
C. \({\tan ^2}\alpha = \frac{1}{3}\).
D. \({\cos ^2}\alpha = \frac{1}{4}\).
+ \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) nên tính được \({\cos ^2}\alpha \), cos\(\alpha \).
+ \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\) nên tính được tan \(\alpha \).
Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\) nên \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{1}{2}} \right)^2} = \frac{3}{4}\)
Do \(\alpha \) là góc nhọn nên cos\(\alpha \)>0, \(\cos \alpha = \frac{{\sqrt 3 }}{2}\).
Lại có: \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{\frac{1}{2}}}{{\frac{{\sqrt 3 }}{2}}} = \frac{{\sqrt 3 }}{3}\) nên \({\tan ^2}\alpha = \frac{1}{3}\)
Chọn C

Các bài tập cùng chuyên đề
Bài 1 :
Tính số đo góc nhọn \(\alpha \) biết \(10{\sin ^2}\alpha + 6{\cos ^2}\alpha = 8\).
-
A.
\(\alpha = {30^0}.\)
-
B.
\(\alpha = {45^0}.\)
-
C.
\(\alpha = {60^0}.\)
-
D.
\(\alpha = {120^0}.\)
Bài 2 :
Cho tam giác ABC vuông cân tại A và \(AB = AC = a\) (H.4.7a).
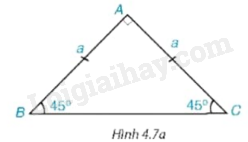
a) Hãy tính BC và các tỉ số \(\frac{{AB}}{{BC}}\) và \(\frac{{AC}}{{BC}}.\) Từ đó suy ra \(\sin {45^0};\cos {45^0}.\)
b) Hãy tính các tỉ số \(\frac{{AB}}{{AC}}\) và \(\frac{{AC}}{{AB}}.\) Từ đó suy ra \(\tan {45^0};\cot {45^0}.\)
Bài 3 :
Xét tam giác đều ABC có cạnh bằng 2a.
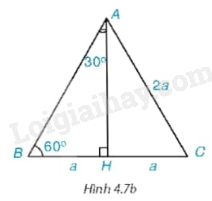
a) Tính đường cao AH của tam giác ABC (H.4.7b) .
b) Tính \(\sin {30^0};\cos {30^0};\sin {60^0};\cos {60^0}.\)
c) Tính \(\tan {30^0};\cot {30^0};\tan {60^0};\cot {60^0}.\)
Bài 4 :
Cho tam giác ABC vuông tại A có \(\widehat C = {45^0}\) và \(AB = c.\) Tính BC và AC theo c.
Bài 5 :
Cho tam giác vuông có 1 góc nhọn \({60^0}\) và cạnh kề với góc \({60^0}\) bằng 3 cm. Hãy tính cạnh đối của góc này.
Bài 6 :
Cho tam giác vuông có một góc nhọn bằng \({30^0}\) và cạnh đối với góc này bằng 5 cm. Tính độ dài cạnh huyền của tam giác.
Bài 7 :
Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và \(\sqrt 3 .\) Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69) .
Bài 8 :
Giá trị \(\tan {30^0}\) bằng
A. \(\sqrt 3 \)
B. \(\frac{{\sqrt 3 }}{2}\)
C. \(\frac{1}{{\sqrt 3 }}\)
D. 1
Bài 9 :
Tính giá trị biểu thức sau:
a) \(A = \frac{{\sin {{30}^o}.\cos {{30}^o}}}{{\cot {{45}^o}}}\)
b) \(B = \frac{{\tan {{30}^o}}}{{\cos {{45}^o}.\cos {{60}^o}}}\)
Bài 10 :
Tính giá trị biểu thức:
a) A = \(4 - {\sin ^2}{45^o} + 2{\cos ^2}{60^o} - 3{\cot ^3}{45^o}\)
b) B = \(\tan {45^o}.\cos {30^o}.\cot {30^o}\)
c) C = \(\sin {15^o} + \sin {75^o} - cos{15^o} - co{\mathop{\rm s}\nolimits} {75^o} + \sin {30^o}\)
Bài 11 :
Sử dụng bảng tỉ số lượng giác của các góc nhọn đặc biệt, tính giá trị của biểu thức:
\(\sin 60^\circ - \cos 60^\circ .\tan 60^\circ \).
Bài 12 :
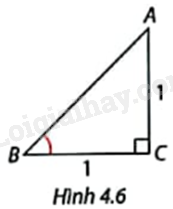
Trong Hình 4.6, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B.
Bài 13 :
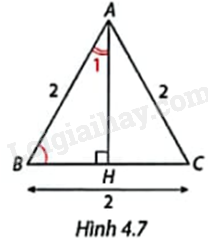
Trong Hình 4.7, tam giác ABC là tam giác gì? Xác định số đo và các tỉ số lượng giác của góc B và góc \({A_1}\).
Bài 14 :
Trong Hình 4.9, hãy tính các tỉ số \(\frac{{PN}}{{PQ}}\) và \(\frac{{PN}}{{PM}}\), từ đó tìm \(\frac{{PQ}}{{PM}}\).

Bài 15 :
Góc nhọn \(\alpha \) có \(\cot \alpha = \sqrt 3 \). Số đo của góc \(\alpha \) là
A. \({30^o}\).
B. \({60^o}\).
C. \({45^o}\).
D. \({75^o}\).
Bài 16 :
Số \(\frac{1}{{\sqrt 3 }}\) là giá trị của
-
A.
\(\cot 30^\circ \).
-
B.
\(\cos 45^\circ \).
-
C.
\(\sin 45^\circ \).
-
D.
\(\tan 30^\circ \).
Bài 17 :
Dùng bảng lượng giác, tính góc nhọn \(\alpha \) biết rằng \(\sin \alpha = \sqrt 3 \cos \alpha \).
-
A.
\(0^\circ \).
-
B.
\(30^\circ \).
-
C.
\(45^\circ \).
-
D.
\(60^\circ \).
Bài 18 :
Cho tam giác ABC vuông tại A có \(AC = 5\sqrt 3 cm\), \(AB + BC = 15cm\). Tính \(\tan \frac{B}{2}\).
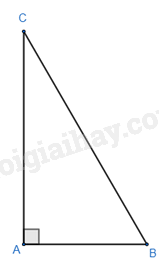
-
A.
\(\sqrt 3 \).
-
B.
\(\frac{{\sqrt 3 }}{2}\).
-
C.
\(\frac{{\sqrt 3 }}{3}\).
-
D.
\(\frac{1}{2}\).
Bài 19 :
Tính giá trị các biểu thức sau:
a) \(P = \frac{{\tan {{60}^o}.\cot {{30}^o}}}{{6\sin {{30}^o}}}\)
b) \(Q = \frac{{\sin {{45}^o}.\cos {{45}^o}}}{{\sin {{30}^o}.c{\rm{os6}}{{\rm{0}}^o}}}\)
Bài 20 :
Hai trụ điện cùng chiều cao được dựng thẳng đứng ở hai bên lề đối diện một đại lộ rộng 80 m (AC = 80 m). Từ một điểm M trên mặt đường giữa hai trụ người ta nhìn thấy đỉnh hai trụ điện với các góc nâng lần lượt là 60o và 30o. Tính chiều cao của trụ điện và khoảng cách từ điểm M đến gốc mỗi trụ điện.
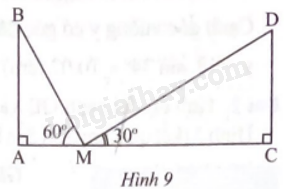
Bài 21 :
Sử dụng bảng tỉ số lượng giác của các góc nhọn đặc biệt, tính giá trị của mỗi biểu thức sau:
a) \(2sin30^\circ - 2cos{\rm{ }}60^\circ + tan{\rm{ }}45^\circ \)
b) \(sin{\rm{ }}45^\circ {\rm{ }} + {\rm{ }}cot{\rm{ }}60^\circ .{\rm{ }}cos{\rm{ }}30^\circ \)
Bài 22 :
a) Tính các góc của tam giác vuông có một góc nhọn có tang bằng \(\frac{{\sqrt 3 }}{3}\).
b) Một hình chữ nhật có kích thước 3 và \(\sqrt 3 \). Tính các góc tạo bởi đường chéo và cạnh của hình chữ nhật đó.
Bài 23 :
Xét tam giác ABC vuông tại B, có \(\widehat A = {30^o}\). Tia Bt sao cho \(\widehat {CBt} = {30^o}\) cắt tia AC ở D, D nằm giữa A và C. Chứng minh rằng khoảng cách từ D đến đường thẳng BC bằng \(\frac{{AB}}{4}\).
Bài 24 :
Xét điểm B nằm giữa hai điểm A và H. Giả sử có điểm D sao cho DH vuông góc với AB và \(\widehat {DAH} = {15^o},\widehat {DBH} = {30^o}\). Chứng minh rằng \(HD = \frac{{AB}}{2}\).
Bài 25 :
Tìm độ dài dây cáp mắc giữa hai cọc ở vị trí C, D trên hai bên bờ vực như trong Hình 4.21 (làm tròn đến mét).
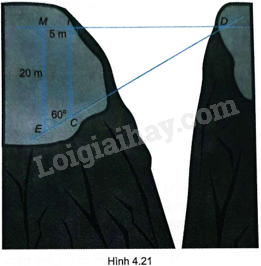
Bài 26 :
Giá trị của biểu thức B = tan 45o .cos 30o. cot 30o là
A. \(\frac{{\sqrt 3 }}{3}\)
B. \(\frac{{\sqrt 6 }}{2}\)
C. \(\frac{{\sqrt 3 }}{2}\)
D. \(\frac{3}{2}\)
Bài 27 :
Cho tam giác vuông có một góc nhọn \({60^o}\) và cạnh kề với góc \({60^o}\) bằng 3cm. Hãy tính cạnh đối của góc này.
Bài 28 :
Cho tam giác vuông có một góc nhọn \({30^o}\) và cạnh đối với góc này bằng 5cm. Tính độ dài cạnh huyền của tam giác
Bài 29 :
Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và \(\sqrt 3 \). Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác của các góc đặc biệt).
Bài 30 :
Giá trị \(\tan {30^o}\) bằng
A. \(\sqrt 3 \).
B. \(\frac{{\sqrt 3 }}{2}\).
C. \(\frac{1}{{\sqrt 3 }}\).
D. 1.


















Danh sách bình luận