Cho hình chóp S. ABCD có đáy là tứ giác ABCD có hai cạnh đối diện không song song. Lấy điểm M thuộc miền trong của tam giác SCD. Tìm giao tuyến của mặt phẳng (ABM) và mặt phẳng (SAC).
Nếu hai mặt phân biệt (P) và (Q) có điểm chung thì chúng có một đường thẳng chung duy nhất d chứa tất cả các điểm chung của hai mặt phẳng đó. Đường thẳng d đó gọi là giao tuyến của hai mặt phẳng (P) và (Q), kí hiệu \(d = \left( P \right) \cap \left( Q \right)\).
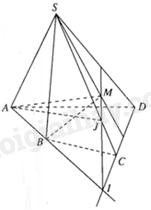
Trong mặt phẳng (ABCD), gọi I là giao điểm của AB và CD.
Vì \(I \in AB \Rightarrow I \in \left( {ABM} \right),I \in SC \Rightarrow I \in \left( {SCD} \right)\).
Trong mặt phẳng (SAC), gọi J là giao điểm của IM và SC.
Ta có: \(J \in SC \Rightarrow J \in mp\left( {SAC} \right),J \in IM \Rightarrow J \in mp\left( {ABM} \right)\).
Lại có: \(A \in mp\left( {SAC} \right),A \in mp\left( {ABM} \right)\).
Do đó, giao tuyến của mặt phẳng (ABM) và mặt phẳng (SAC) là đường thẳng AJ.

Các bài tập cùng chuyên đề


















Danh sách bình luận