Cho hình chữ nhật ABCD có chu vi bằng 36 cm. Gọi M là trung điểm của cạnh BC. Biết rằng MA ⊥ MD. Tính độ dài các cạnh của hình chữ nhật ABCD (H.3.36).
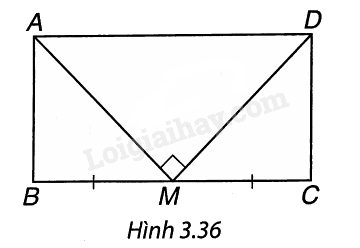
- Chứng minh \(\Delta AMB = \Delta DMC\).
- Chứng minh AB = BM = MC = CD, ta tính được các cạnh của hình chữ nhật.
Hai tam giác vuông AMB và DMC có AB = DC, BM = MC nên \(\Delta AMB = \Delta DMC(c.g.c) \Rightarrow \widehat {AMB} = \widehat {DMC}.\)
Do góc \(\widehat {AMD} = 90^\circ \Rightarrow \widehat {AMB} = \widehat {DMC} = \left( {180^\circ - 90^\circ } \right):2 = 45^\circ .\)
Do đó ∆AMB vuông cân tại B, ∆DMC vuông cân tại C.
Suy ra AB = BM = MC = CD.
Ta có AD = BC = 2AB, suy ra chu vi của ABCD bằng
AB + BC + CD + DA = 36
Do đó AB = CD = 36 : 6 = 6 cm, AD = CB = 12 cm.
Các bài tập cùng chuyên đề
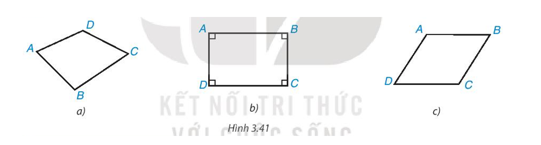
Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao?
Bằng ê ke, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.
Bằng compa, nêu cách kiểm tra một tứ giác có là hình chữ nhật hay không. Hãy giải thích kết quả.
Tìm bốn ví dụ về hình chữ nhật trong thực tế
Cho biết số đo mỗi góc của tứ giác ABCD ở Hình 47
Cho biết số đo mỗi góc của tứ giác ABCD ở Hình 47
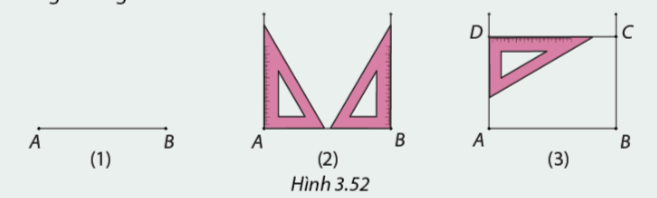
Ta đã được học cách vẽ các hình tứ giác đặc biệt. Em hãy cho biết khi thực hiện các bước vẽ như trong Hình 3.52, ta được tứ giác ABCD là hình gì. Góc C có là góc vuông không?
Trong hình chữ nhật có chu vi 100m, hình nào có diện tích lớn nhất? Tính diện tích đó.
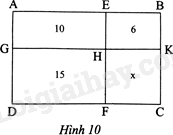
Hình chữ nhật ABCD được chia thành bốn hình chữ nhật nhỏ như Hình 10. Biết diện tích ba hình chữ nhật nhỏ lần lượt là \(10c{m^2},15c{m^2},6c{m^2}\). Tính diện tích \(x\left( {c{m^2}} \right)\) của hình chữ nhật nhỏ còn lại.
