Cho tam giác ABC, trung tuyến AI. Tia phân giác của góc AIB và tia phân giác góc AIC cắt AB, AC lần lượt tại M và N. Chứng minh MN//BC.
+ Sử dụng kiến thức về tính chất đường phân giác của tam giác để chứng minh \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\): Trong tam giác, đường phân giác của một góc chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề với hai đoạn thẳng ấy.
+ Sử dụng kiến thức về định lí Thalès đảo để chứng minh MN//BC: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
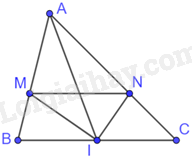
Tam giác ABI có IM là phân giác của góc AIB nên \(\frac{{MA}}{{MB}} = \frac{{AI}}{{BI}}\) (1) (tính chất đường phân giác của tam giác)
Tam giác ACI có IN là phân giác của góc AIC nên \(\frac{{NA}}{{NC}} = \frac{{AI}}{{CI}}\) (2) (tính chất đường phân giác của tam giác)
Vì AI là trung tuyến của tam giác ABC nên \(BI = CI\) (3)
Từ (1), (2), (3) ta có: \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\)
Tam giác ABC có: \(\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}}\) nên MN//BC (định lí Thalès đảo)

Các bài tập cùng chuyên đề
Bài 1 :
Hãy chọn câu đúng. Tỉ số \(\dfrac{x}{y}\) của các đoạn thẳng trong hình vẽ, biết rằng các số trên hình cùng đơn vị đo là $cm$ .
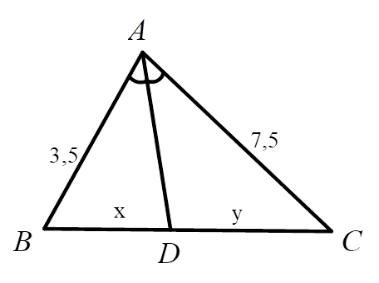
-
A.
\(\dfrac{7}{{15}}\)
-
B.
\(\dfrac{1}{7}\)
-
C.
\(\dfrac{{15}}{7}\)
-
D.
\(\dfrac{1}{{15}}\)
Bài 2 :
Cho tam giác $ABC$ , $AC = 2AB$ , $AD$ là đường phân giác của tam giác $ABC$ , khi đó \(\dfrac{{BD}}{{CD}} = ?\)
-
A.
\(\dfrac{{BD}}{{CD}} = 1\)
-
B.
\(\dfrac{{BD}}{{CD}} = \dfrac{1}{3}\)
-
C.
\(\dfrac{{BD}}{{CD}} = \dfrac{1}{4}\)
-
D.
\(\dfrac{{BD}}{{CD}} = \dfrac{1}{2}\)
Bài 3 :
Cho hình vẽ, biết các số trên hình cùng đơn vị đo. Tỉ số \(\dfrac{x}{y}\) bằng:
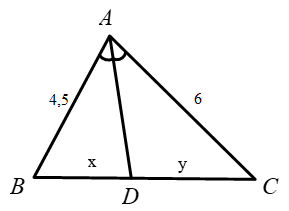
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{2}{3}\)
-
C.
\(\dfrac{4}{3}\)
-
D.
Chưa đủ dữ kiện kết luận
Bài 4 :
Cho tam giác \(ABC\), \(AC = 2AB\), \(AD\) là đường phân giác của tam giác\(ABC\). Xét các khẳng định sau, số khẳng định đúng là:
(I) \(\dfrac{{BD}}{{DC}} = \dfrac{1}{2}\) (II) \(\dfrac{{DC}}{{BC}} = \dfrac{2}{3}\) (III) \(\dfrac{{BD}}{{BC}} = \dfrac{1}{2}\)
-
A.
\(0\)
-
B.
\(3\)
-
C.
\(1\)
-
D.
\(2\)
Bài 5 :
Cho tam giác ABC có \(AB < AC,\) AD là đường phân giác. Khi đó:
-
A.
\(BD < DC\)
-
B.
\(BD > DC\)
-
C.
\(BD = DC\)
-
D.
Không so sánh được
Bài 6 :
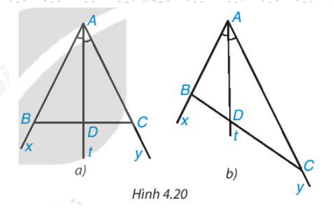
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D.
Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\)
Bài 7 :
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D
Khi lấy B và C sao cho AB = 2 cm và AC = 4 cm (H.4.20b), hãy dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC rồi so sánh hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\)
Bài 8 :
Tính độ dài x trên Hình 4.23
Bài 9 :
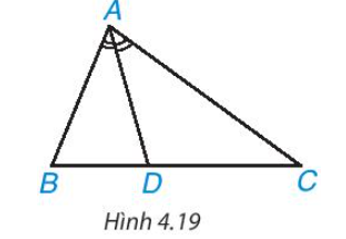
Trong H.4.19, AD là đường phân giác của tam giác ABC. Hai tỉ số \(\dfrac{{DB}}{{DC}}\) và \(\dfrac{{AB}}{{AC}}\) có bằng nhau không?
Bài 10 :
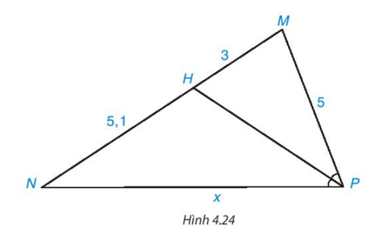
Tính độ dài x trên Hình 4.24.
Bài 11 :
Cho tam giác ABC. Đường phân giác trong của góc A cắt BC tại D. Tính độ dài đoạn thẳng DC biết AB = 4,5 m; AC = 7,0 m và CB = 3,5 m (làm tròn kết quả đến hàng phần chục).
Bài 12 :
Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là
A. 3 cm.
B. 6 cm.
C. 9 cm.
D. 12 cm.
Bài 13 :
Tính độ dài x trong Hình 5.12
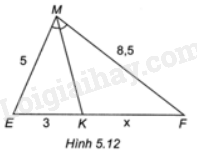
Bài 14 :
Cho \(\Delta ABC\) có AD, BE, CF lần lượt là đường phân giác của góc A, góc B, góc C \(\left( {D \in BC,E \in AC,F \in AB} \right)\). Chứng minh rằng \(\frac{{AE}}{{EC}}.\frac{{CD}}{{DB}}.\frac{{BF}}{{FA}} = 1\).
Bài 15 :
Cho tam giác ABC, phân giác AD \(\left( {D \in BC} \right)\). Kẻ DE//AB\(\left( {E \in AC} \right)\). Chứng minh rằng \(AB.EC = AC.EA\)
Bài 16 :
Cho \(\Delta ABC\). Tia phân giác góc trong của góc A cắt BC tại D. Cho \(AB = 6,AC = x,BD = 9,BC = 21\). Độ dài x bằng
A. 4
B. 6
C. 12
D. 14
Bài 17 :
Cho tam giác ABC có AD là tia phân giác của góc BAC. Biết \(AB = 3cm,BD = 4cm,CD = 6cm\). Độ dài AC bằng
A. 4cm
B. 5cm
C. 6cm
D. 4,5cm
Bài 18 :
Cho hình thoi ABCD có M là trung điểm của AD, đường chéo AC cắt BM tại điểm E (H.5.16)
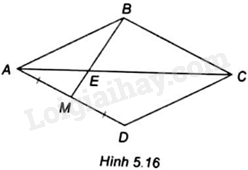
Tỉ số \(\frac{{EM}}{{EB}}\) bằng
A. \(\frac{1}{3}\)
B. 2
C. \(\frac{1}{2}\)
D. \(\frac{2}{3}\)
Bài 19 :
Cho tam giác ABC cân tại A, các đường phân giác BD, CE \(\left( {D \in AC,E \in AB} \right)\). Chứng minh DE//BC
Bài 20 :
Quan sát Hình 4.17 và chọn khẳng định đúng.
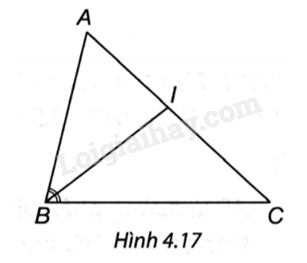
A. \(\frac{{IA}}{{IC}} = \frac{{BA}}{{AC}}.\)
B. \(\frac{{IA}}{{IC}} = \frac{{BC}}{{BA}}.\)
C. \(\frac{{IA}}{{IC}} = \frac{{BA}}{{BC}}.\)
D. \(\frac{{IA}}{{IC}} = \frac{{AC}}{{AB}}.\)
Bài 21 :
Quan sát Hình 4.18, biết BI là phân giác của góc B, AB = 12 cm, BC = 15 cm, AC = 9 cm. Độ dài đoạn IA là:

A. 5 cm.
B. 4 cm.
C. 6 cm.
D. 3 cm.
Bài 22 :
Quan sát Hình 4.19. Tỉ số \(\frac{x}{y}\) bằng
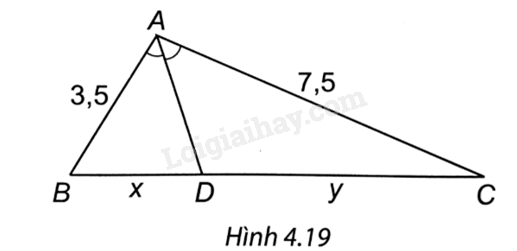
A. \(\frac{1}{7}\).
B. \(\frac{{15}}{7}\)
C. \(\frac{7}{{15}}\)
D. \(\frac{2}{{15}}\)
Bài 23 :
Quan sát Hình 4.20. Độ dài x, y lần lượt là:
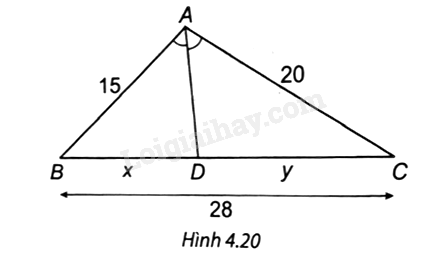
A. x = 16 cm; y = 12 cm.
B. x = 14 cm; y = 14 cm.
C. x = 14,3 cm; y = 10,7 cm.
D. x = 12 cm; y = 16 cm.
Bài 24 :
Tìm độ dài x trong Hình 4.21.
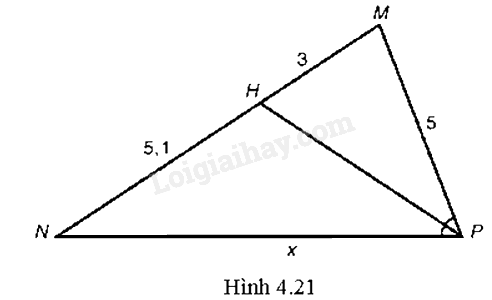
Bài 25 :
Cho tam giác ABC. Đường phân giác của góc A cắt BC tại D. Tính độ dài đoạn thẳng DC biết AB = 4,5 m; AC = 7,0 m và CB = 3,5 m (làm tròn kết quả đến hàng phần chục).
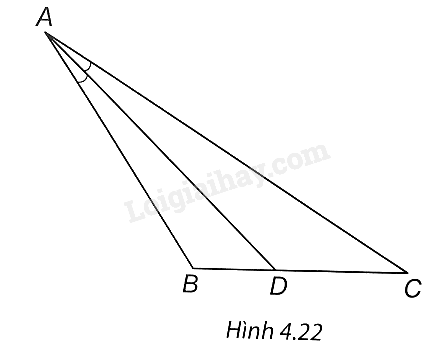
Bài 26 :
Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng \(\frac{{AC}}{{AB}} = \frac{{EC}}{{EA}}.\)
Bài 27 :
Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.
a) Tính độ dài các đoạn thẳng DB và DC.
b) Tính tỉ số diện tích của hai tam giác ABD và ACD.
Bài 28 :
Tính độ dài cạnh \(MQ\) của tam giác \(MPQ\) trong Hình 6.
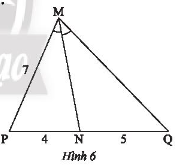
Bài 29 :
Tính độ dài \(x\) trong Hình 7.

Bài 30 :
Tam giác \(ABC\) có \(AB = 6cm,AC = 8cm,BC = 10cm\). Đường phân giác của góc \(BAC\) cắt cạnh \(BC\) tại \(D\).
a) Tính độ dài các đoạn thẳng \(DB\) và \(DC\).
b) Tính tỉ số diện tích giữa \(\Delta ADB\) và \(\Delta ADC\).



















Danh sách bình luận