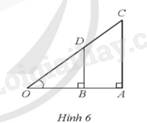
Cho Hình 6 có AB = 3 cm, CD = 4 cm. Tính số đo góc AOC (làm tròn kết quả đến hàng đơn vị của độ).
Bước 1: Chứng minh \(BD//CA\), sau đó áp dụng định lý Thales để suy ra \(\frac{{OA}}{{OB}} = \frac{{OC}}{{OD}}\).
Bước 2: Áp dụng tính chất dãy tỉ số bằng nhau: \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{OA - OB}}{{OC - OD}} = \frac{{AB}}{{CD}} = \frac{3}{4}\)
Bước 3: \(\cos \widehat {AOC} = \frac{{OA}}{{OC}}\), từ đó suy ra số đo góc AOC.
Ta có: \(BD \bot OA,CA \bot OA\) nên \(BD//CA\).
Xét tam giác OAC có \(BD//CA\), áp dụng định lý Thales, ta được: \(\frac{{OA}}{{OB}} = \frac{{OC}}{{OD}}\)
Suy ra \(\frac{{OA}}{{OC}} = \frac{{OB}}{{OD}} = \frac{{OA - OB}}{{OC - OD}} = \frac{{AB}}{{CD}} = \frac{3}{4}\)
Vì tam giác OAC vuông tại A nên ta có \(\cos \widehat {AOC} = \frac{{OA}}{{OC}} = \frac{3}{4}\), do đó \(\widehat {AOC} \approx 41^\circ \).

Các bài tập cùng chuyên đề
Bài 1 :
Dùng MTCT, tìm các góc \(\alpha \) (làm tròn đến phút) , biết:
a) \(\sin \alpha = 0,3782;\)
b) \(\cos \alpha = 0,6251;\)
c) \(\tan \alpha = 2,154;\)
d) \(\cot \alpha = 3,253.\)
Bài 2 :
Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút) , biết rằng:
a) \(\sin x = 0,2368;\)
b) \(\cos x = 0,6224;\)
c) \(\tan x = 1,236;\)
d) \(\cot x = 2,154.\)
Bài 3 :
Sử dụng máy tính cầm tay, tìm góc nhọn \(\alpha \) trong mỗi trường hợp sau đây:
a) cos\(\alpha \) = 0,6
b) tan\(\alpha \) = \(\frac{3}{4}\)
Bài 4 :
Tìm số đo góc \(\alpha \), biết rằng:
a) sin\(\alpha \) = 0,25
b) cos\(\alpha \) = 0,75
c) tan\(\alpha \) = 1
d) cot\(\alpha \) = 2.
Bài 5 :
Sử dụng máy tính cầm tay, hãy tìm góc nhọn \(\alpha \), biết:
a) \(\cos \alpha = 0,8\);
b) \(\tan \alpha = 5\).
Làm tròn kết quả đến giây.
Bài 6 :
Xác định số đo góc nhọn A của tam giác vuông ABC trong mỗi trường hợp ở Hình 4.12. Làm tròn kết quả đến độ.

Bài 7 :
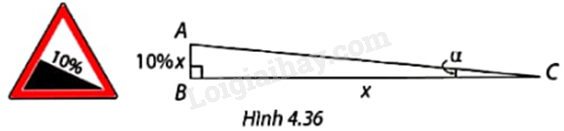
Trong các biển báo dốc nguy hiểm, độ nghiêng của dốc thường được ghi ở dạng phần trăm. Chẳng hạn độ nghiêng 10% nghĩa là dốc có chiều cao AB bằng 10% độ dài BC (Hình 4.36). Dốc 10% có góc nghiêng \(\alpha \) so với phương nằm ngang (làm tròn đến đơn vị độ) là
A. \({12^o}\).
B. \({10^o}\).
C. \({8^o}\).
D. \({6^o}\).
Bài 8 :
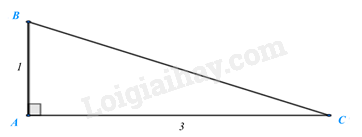
(Làm tròn đến hàng đơn vị) Số đo góc C khoảng
-
A.
\(18^\circ \).
-
B.
\(71^\circ \).
-
C.
\(19^\circ \).
-
D.
\(72^\circ \).
Bài 9 :
Để vẽ một tam giác cân có góc ở đáy là \(50^\circ \) mà không có thước đo góc, An vẽ một tam giác cân có cạnh bên là 3cm và cạnh đáy là 4cm. Góc ở đáy của tam giác cân này có sai số so với \(50^\circ \) là bao nhiêu? (làm tròn đến phút)
-
A.
\(1^\circ 47'\).
-
B.
\(1^\circ 48'\).
-
C.
\(1^\circ 49'\).
-
D.
\(1^\circ 50'\).
Bài 10 :
Tìm các góc nhọn x, y, z trong mỗi trường hợp sau (kết quả làm tròn đến hàng đơn vị của phút):
a) cos x = 0,435
b) sin y = 0,451
c) tan z = 4,12
d) cot m = 0,824
Bài 11 :
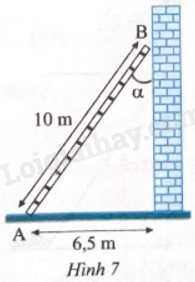
Một cái thang dài 10 m đặt dựa vào tường sao cho chân thang cách tường 6,5 m (Hình 7). Tìm góc \(\alpha \) tạo bởi thang và tường (kết quả làm tròn đến hàng đơn vị của độ).
Bài 12 :
Một màn hình ti vi có kích thước như trong Hình 8. Tính góc giữa đường chéo và hai cạnh.

Bài 13 :
Hãy dùng MTCT, tìm số đo góc nhọn \(\alpha \) (làm tròn đến độ) trong mỗi trường hợp
a) Khi sin \(\alpha \) lần lượt bằng \(\frac{1}{4},\frac{1}{3},\frac{1}{2},\frac{2}{3};\)
b) Khi cos \(\alpha \) lần lượt bằng \(\frac{1}{4},\frac{1}{3},\frac{1}{2},\frac{2}{3}\).
Bài 14 :
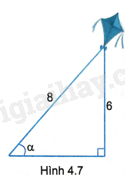
Một cái diều có dây diều dài 8m, khi dây diều căng thì diều bay ở độ cao 6m. Hỏi khi đó dây diều tạo với phương ngang của mặt đất góc nhọn \(\alpha \) xấp xỉ bằng bao nhiêu độ (H.4.7)?
Bài 15 :
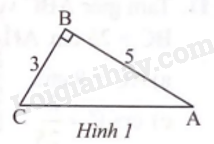
Số đo góc C trong Hình 1 (kết quả làm tròn đến hằng phần trăm của độ) là
A. \({59,04^o}\)
B. \({30,93^o}\)
C. \({36,87^o}\)
D. \({53,13^o}\)
Bài 16 :
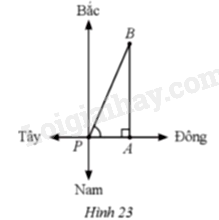
Một thuyền đi với tốc độ 20km/h theo hướng Đông trong 1 giờ 30 phút từ vị trí P đến vị trí A. Sau đó nó sẽ đi theo hướng Bắc với cùng tốc độ trong 3 giờ 30 phút đến vị trí B (Hình 23). Tính góc so với hướng Đông mà thuyền đi từ vị trí P đến vị trí B (làm tròn kết quả đến hàng đơn vị của phút).
Bài 17 :
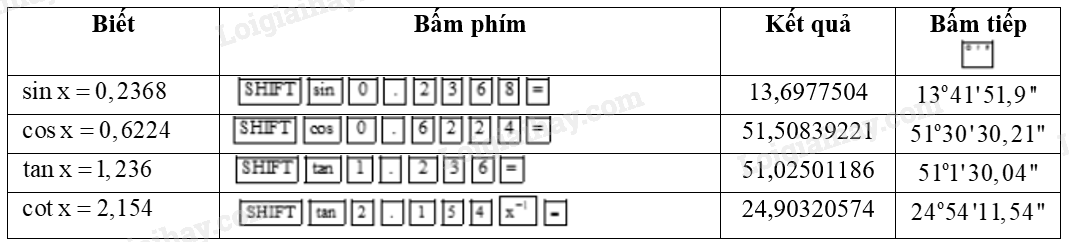
Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút), biết rằng:
a) \(\sin x = 0,2368\);
b) \(\cos x = 0,6224\);
c) \(\tan x = 1,236\);
d) \(\cot x = 2,154\).
Hướng dẫn (HD)
Bài 18 :
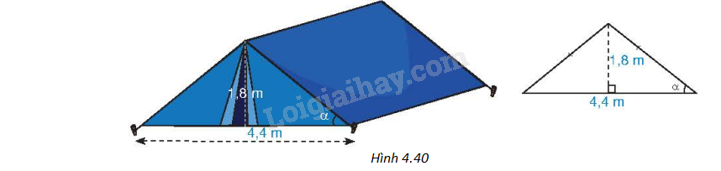
Hình 4.40 là mô hình của một túp lều. Tìm góc \(\alpha \) giữa cạnh mái lều và mặt đất (làm tròn kết quả đến phút).
Bài 19 :
Cho tam giác ABC vuông tại A có AB = 5, BC = 8. Số đo góc C là: (làm tròn đến độ)
-
A.
\(\widehat C \approx 52^\circ \).
-
B.
\(\widehat C \approx 38^\circ \).
-
C.
\(\widehat C \approx 51^\circ \).
-
D.
\(\widehat C \approx 39^\circ \).
Bài 20 :
Biết \(\cos \alpha = \frac{1}{2}\) thì \(\alpha \) bằng
-
A.
\(35^\circ \).
-
B.
\(45^\circ \).
-
C.
\(30^\circ \).
-
D.
\(60^\circ \).
Bài 21 :
Tam giác ABC vuông tại A có AC = 6cm; BC = 12cm. Số đo góc ACB bằng
-
A.
\(30^\circ \).
-
B.
\(45^\circ \).
-
C.
\(60^\circ \).
-
D.
\(90^\circ \).
Bài 22 :
Một khối u của một căn bệnh nhân cách mặt da 5,7cm, được chiếu bởi một chùm tia gamma. Để tránh làm tổn thương mô, bác sĩ đặt nguồn tia cách khối u (trên mặt da) 8,3cm (hình vẽ)
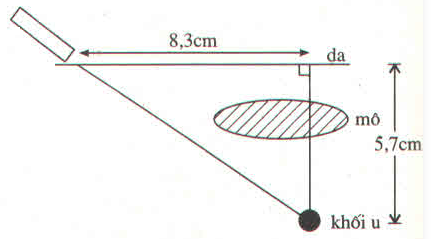
Tính góc tạo bởi chùm tia với mặt da và chùm tia phải đi một đoạn dài bao nhiêu để đến được khối u?
Bài 23 :
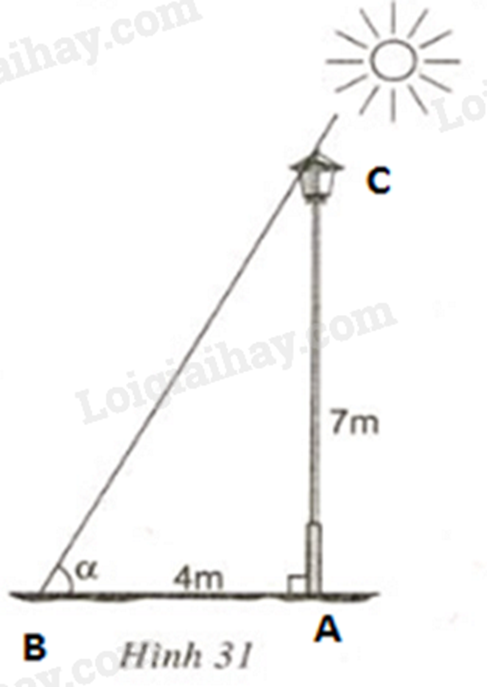
Một cột đèn cao 7m có bóng trên mặt đất dài 4m. Hãy tính góc (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất (góc \(\alpha \) trong hình 31).


















Danh sách bình luận