Chứng minh rằng trong một tứ giác, độ dài mỗi cạnh bé hơn tổng độ dài ba cạnh còn lại.
Ta sử dụng bất đẳng thức trong tam giác.
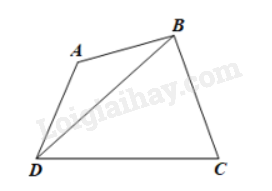
Xét tứ giác ABCD như hình vẽ. Ta cần chứng minh \(AB < AD + BC + CD\) và các trường hợp còn lại tương tự.
Xét tam giác ABD, ta có: \(AB < AD + DB\) (bất đẳng thức trong tam giác).
Xét tam giác BCD, ta có: \(DB < BC + CD\) (bất đẳng thức trong tam giác).
Do đó \(AB < AD + DB < AD + BC + CD.\)
Vậy \(AB < AD + BC + CD.\)
Tương tự ta cũng có:
\(BC < AB + CD + DA;CD < AD + AB + BC;DA < AB + BC + CD\).

Các bài tập cùng chuyên đề
Bài 1 :
Trong các hình tạo bởi bốn đoạn thẳng \(AB\), \(BC\), \(CD\) và \(DA\) sau đây, hình nào không có hai đoạn thẳng cùng nằm trên một đường thẳng?

Bài 2 :
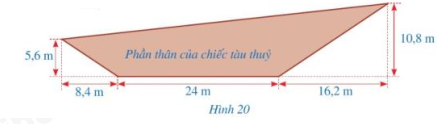
Một chiếc tàu thủy có mặt cắt dọc phần nổi trên mặt nước của thân tàu được mô tả ở Hình 20. Tính chu vi mặt cắt dọc phần nổi trên mặt nước của thân tàu đó (làm tròn kết quả đến hàng phần mười của mét).
Bài 3 :
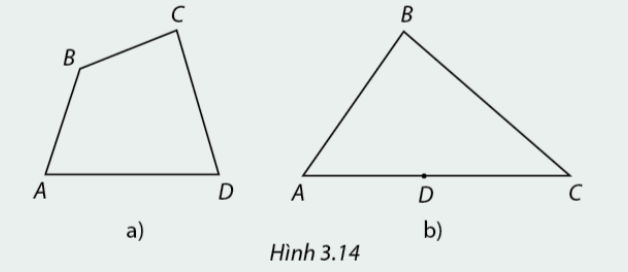
Ta đã được học về tứ giác. Em hãy cho biết trong trường hợp nào của Hình 3.14, bốn đoạn thẳng AB, BC và AD tạo thành một tứ giác.
Bài 4 :
Viết tên hai tứ giác có đỉnh là bốn trong năm điểm \(A,B,C,D,E\) trong Hình 3.22.

Bài 5 :
Chọn phương án đúng.
Trong các khẳng định sau, khẳng định nào đúng?
A. Không có tứ giác nào mà không có góc tù.
B. Nếu tứ giác có ba góc nhọn thì góc còn lại là góc tù.
C. Nếu tứ giác có hai góc tù thì hai góc còn lại phải nhọn.
D. Không có tứ giác nào có ba góc tù.
Bài 6 :
Bài 7 :
Chọn câu đúng nhất trong các câu sau khi định nghĩa tứ giác ABCD.
-
A.
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA.
-
B.
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA, trong đó bất kì hai đoạn thẳng nào cũng không nằm trên cùng nằm trên một đường thẳng.
-
C.
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó hai đoạn thẳng kề một đỉnh song song với nhau.
-
D.
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA và bốn góc tại đỉnh bằng nhau.
Bài 8 :
Cho tứ giác ABCD. Chọn khẳng định sai trong các khẳng định sau:
-
A.
Hai cạnh kề nhau của tứ giác là AB, BC.
-
B.
Hai cạnh đối nhau của tứ giác là BC, DA.
-
C.
Hai góc đối nhau của tứ giác là \(\widehat C\) và \(\widehat D\).
-
D.
Hai góc kề một đáy của tứ giác là \(\widehat A\) và \(\widehat B\).
Bài 9 :
Cho tứ giác \(ABCD\). Khẳng định nào sau đây là sai?
-
A.
\(AB\) và \(BC\) là hai cạnh kề nhau.
-
B.
\(BC\) và \(AD\) là hai cạnh đối nhau.
-
C.
\(\widehat A\) và \(\widehat B\) là hai góc đối nhau.
-
D.
\(AC\) và \(BD\) là hai đường chéo.
Bài 10 :
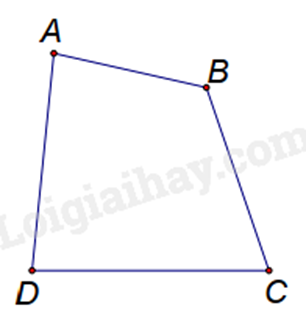
Cho tứ giác ABCD như hình vẽ, chọn câu đúng:
-
A.
Các điểm A, B, C, D gọi là các đỉnh.
-
B.
Hai cạnh kề nhau là AB và CD.
-
C.
Hai góc đối nhau là \(\widehat A\) và \(\widehat D\).
-
D.
AC và BD là hai cạnh chéo nhau.


















Danh sách bình luận