Một số bằng tổng các ước của nó (không kể chính nó) gọi là số hoàn hảo.
Chẳng hạn, các ước của 6 (không kể chính nó) là 1; 2; 3; ta có: 1 + 2 + 3 = 6.
Vậy 6 là số hoàn hảo. Em hãy chỉ ra trong các số 10; 28; 496; số nào là số hoàn hảo.
Cho đến năm 2018, người ta mới tìm được 51 số hoàn hảo. Số hoàn hảo thứ 51 là số có 49 724 095 chữ số.
Kiểm tra các ước của các số đã cho (không kể chính nó) và tính tổng các ước của chúng
+ Các ước của 10 (không kể chính nó) là 1; 2; 5 nhưng 1 + 2 + 5 = 8 ≠ 10 nên 10 không là số hoàn hảo.
+ Các ước của 28 (không kể chính nó) là: 1; 2; 4; 7; 14 và 1 + 2 + 4 + 7 + 14 = 28 nên 28 là số hoàn hảo.
+ Các ước của 496 (không kể chính nó) là 1; 2; 4; 8; 16; 31; 62; 124; 248 và 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496 nên 496 là số hoàn hảo.
Vậy trong các số trên có 28 và 496 là số hoàn hảo.
Lời giải hay
Các bài tập cùng chuyên đề
Cho hai số a = 72 và b = 96.
a) Phân tích a và b ra thừa số nguyên tố;
b) Tìm ƯCLN(a, b), rồi tìm ƯC(a, b).
Điền các từ thích hợp vào chỗ chấm:
a) Nếu a ⁝ 7 và b ⁝ 7 thì 7 là……. của a và b.
b) Nếu 9 là số lớn nhất sao cho a ⁝ 9 và b ⁝ 9 thì 9 là …….. của a và b.
a) Số nào là ước chung của 15 và 105 trong các số sau: 1,5,13,15,35,53?
b) Tìm ƯCLN(27,156)
c) Tìm ƯCLN(106,318), từ đó tìm các ước chung của 424 và 636
Tìm các số tự nhiên a,b biết:
a) a+b=192 và ƯCLN(a,b)=24;
b) ab=216 và ƯCLN(a,b) = 6
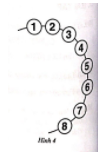
Một số học sinh đứng nắm tay nhau xếp thành hình vòng tròn lớn tham gia hoạt động tập thể. Thầy An đi quanh vòng tròn và gắn cho mỗi học sinh một số thứ tự 1,2,3,4,5,…(Hình 4) và nhận thấy học sinh được gắn số 12 đứng đối diện với học sinh được gắn số 30. Thầy tách các học sinh được gắn số từ số 1 đến số 12 vào nhóm 1, từ số 13 đến số cuối cùng trên vòng tròn vào nhóm 2. Thầy muốn chia các học sinh của mỗi nhóm vào các câu lạc bộ(số câu lạc bộ nhiều hơn 1) sao cho số học sinh ở từng nhóm của mỗi câu lạc bộ là như nhau.
a) Thầy An có bao nhiêu cách để chia học sinh vào các câu lạc bộ?
b) Số câu lạc bộ nhiều nhất mà thầy An có thể chia là bao nhiêu?
