Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2).

a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.
b) Phân tích S thành nhân tử rồi tính S khi \(x = 102m,y = 2m\).
a) Viết biểu thức tính diện tích hình vuông lớn và hình vuông bé: \(S = {a^2}\) với a là độ dài cạnh hình vuông.
Diện tích S của đường bao quanh mảnh vườn = diện tích hình vuông lớn – diện tích hình vuông bé.
b) Phân tích đa thức thành nhân tử bằng cách sử dụng hằng đẳng thức hiệu hai bình phương.
Thay \(x = 102m,y = 2m\) vào đa thức để tìm S.
a) Độ dài cạnh của hình vuông lớn là \(x\).
Suy ra diện tích của hình vuông lớn là \({x^2}\).
Độ dài cạnh của hình vuông bé là \(x-2y\).
Suy ra diện tích của hình vuông bé là \({\left( {x-2y} \right)^2}\).
Diện tích S của đường bao quanh hình vuông là
\(S = {x^2}\;-{\left( {x-2y} \right)^2}\).
b) Ta có \(S = \left[ {x - \left( {x - 2y} \right)} \right]\left[ {x + \left( {x - 2y} \right)} \right]\)
\( = \left( {x - x + 2y} \right)\left( {x + x - 2y} \right) = 2y\left( {2x - 2y} \right)\)
\(= 4y\left( {x - y} \right).\)
Khi \(x = 102m,y = 2m\), ta có \(S = 4.2\left( {102 - 2} \right) = 8.100 = 800\left( {{m^2}} \right).\)

Các bài tập cùng chuyên đề
Bài 1 :
Hiệu bình phương các số lẻ liên tiếp thì luôn chia hết cho
-
A.
7.
-
B.
8.
-
C.
9.
-
D.
10.
Bài 2 :
Chọn câu sai.
-
A.
\(4{x^2} + 4x + 1 = {\left( {2x + 1} \right)^2}\).
-
B.
\(9{x^2} - 24xy + 16{y^2} = {\left( {3x - 4y} \right)^2}\).
-
C.
\(\frac{{{x^2}}}{4} + 2xy + 4{y^2} = {\left( {\frac{x}{2} + 2y} \right)^2}\).
-
D.
\(\frac{{{x^2}}}{4} + 2xy + 4{y^2} = {\left( {\frac{x}{4} + 2y} \right)^2}\).
Bài 3 :
Phân tích các đa thức sau thành nhân tử
a) \({\left( {x + 1} \right)^2} - {y^2}\)
b) \({x^3} + 3{x^2} + 3x + 1\)
c) \(8{x^3} - 12{x^2} + 6x - 1\)
Bài 4 :
Tìm biểu thức thích hợp thay vào mỗi chỗ , từ đó hoàn thành biến đổi sau vào vở để phân tích đa thức sau thành nhân tử:
a) \(4{x^2} - 9 \);
b) \({x^2}{y^2} - \dfrac{1}{4}{y^2}\)
Bài 5 :
Phân tích các đa thức sau thành nhân tử:
a) \(9{x^2} - 16\)
b) \(4{x^2} - 12xy + 9{y^2}\)
c) \({t^3} - 8\)
d) \(2a{x^3}{y^3} + 2a\)
Bài 6 :
Phân tích các đa thức sau thành nhân tử:
a) \(4{x^2} - 1\)
b) \({\left( {x + 2} \right)^2} - 9\)
c) \({\left( {a + b} \right)^2} - {\left( {a - 2b} \right)^2}\)
Bài 7 :
Phân tích các đa thức sau thành nhân tử:
a) \(4{a^2} + 4a + 1\)
b) \( - 3{x^2} + 6xy - 3{y^2}\)
c) \({\left( {x + y} \right)^2} - 2\left( {x + y} \right)z + {z^2}\)
Bài 8 :
Cho \(y > 0\). Tìm độ dài cạnh của hình vuông có diện tích bằng \(49{y^2} + 28y + 4\)
Bài 9 :
Khi phân tích đa thức \(R = 4{x^2} - 4xy + {y^2}\) thành nhân tử thì được:
A. \(R = {(x + 2y)^2}\)
B. \(R = {(x - 2y)^2}\)
C. \(R = {(2x + y)^2}\)
D. \(R = {(2x - y)^2}\)
Bài 10 :
Khi phân tích đa thức \(S = {x^6} - 8\) thành nhân tử thì được:
A. \(S = \left( {{x^2} + 2} \right)\left( {{x^4} - 2{x^2} + 4} \right)\)
B. \(S = \left( {{x^2} - 2} \right)\left( {{x^4} - 2{x^2} + 4} \right)\)
C. \(S = \left( {{x^2} - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)
D. \(S = \left( {x - 2} \right)\left( {{x^4} + 2{x^2} + 4} \right)\)
Bài 11 :
Viết mỗi đa thức sau dưới dạng tích của hai đa thức:
\(a){x^2} - {y^2}\) \(b){x^3} - {y^3}\) \(c){x^3} + {y^3}\)
Bài 12 :
Phân tích mỗi đa thức sau thành nhân tử:
\(a){\left( {x + 2y} \right)^2} - {\left( {2{\rm{x}} - y} \right)^2}\)
\(b)125 + {y^3}\)
\(c)27{{\rm{x}}^3} - {y^3}\)
Bài 13 :
Phân tích mỗi đa thức sau thành nhân tử:
\(a)4{{\rm{x}}^2} - 12{\rm{x}}y + 9{y^2}\)
\(b){x^3} + 9{{\rm{x}}^2} + 27{\rm{x}} + 27\)
\(c)8{y^3} - 12{y^2} + 6y - 1\)
\(d){\left( {2{\rm{x}} + y} \right)^2} - 4{y^2}\)
\(e)27{y^3} + 8\)
\(g)64 - 125{{\rm{x}}^3}\)
Bài 14 :
Dùng hằng đẳng thức “Bình phương của một tổng”, ta có thể phân tích đa thức \({x^2} + 4x + 4\) thành nhân tử như sau:
\({x^2} + 4x + 4 = {\left( {x + 2} \right)^2} = \left( {x + 2} \right).\left( {x + 2} \right)\).
a) Hãy dùng hằng đẳng thức “Hiệu hai bình phương” để phân tích đa thức \({x^2} - 9\) thành nhân tử.
b) Hãy dùng một hằng đẳng thức thích hợp để phân tích đa thức \(8 - {x^3}\) thành nhân tử.
Bài 15 :
Phân tích các đa thức sau thành nhân tử:
a) \({\left( {x - y} \right)^2} - 16{y^2}\)
b) \(27{x^2} - \frac{1}{8}{y^3}\)
Bài 16 :
Độ cao \(h\)(feet) của một vật so với mặt đất sau thời gian \(t\) (giây) kể từ lúc rơi được cho bởi: \(h = 25 - 16{t^2}\)
a) Tìm độ cao của vật so với mặt đất sau 1 giây kể từ lúc rơi.
b) Một học sinh đã viết lại \(h = {\left( {5 - 4{t^2}} \right)^2}\). Học sinh này viết đúng hay sai?
Bài 17 :
Phân tích mỗi đa thức sau thành nhân tử:
a) \(25{x^2} - \frac{1}{4}\)
b) \(36{x^2} + 12xy + {y^2}\)
c) \(\frac{{{x^3}}}{2} + 4\)
d) \(27{y^3} + 27{y^2} + 9y + 1\)
Bài 18 :
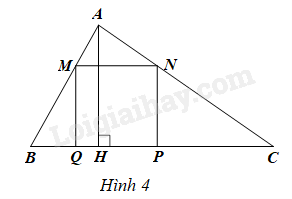
Cho tam giác \(ABC\) có cạnh \(BC = 2x\left( {dm} \right)\), đường cao \(AH = x\left( {dm} \right)\) với \(x > 0\) và hình vuông \(MNPQ\) có cạnh \(MN = y\left( {dm} \right)\) với \(y > 0\) (Hình 4).
a) Viết công thức tính tổng diện tích của các tam giác \(AMN,BMQ,CNP\) dưới dạng tích.
b) Tính tổng diện tích của các tam giác \(AMN,BMQ,CNP\), biết \(x - y = 2\) và \(x + y = 10\)
Bài 19 :
Phân tích đa các đa thức sau thành nhân tử:
a) \(100 - {x^2}\);
b) \(4{x^2} - {y^2}\);
c) \({\left( {x + y} \right)^2} - \frac{1}{4}{y^2}\);
d) \({\left( {x - y} \right)^2} - {\left( {y - z} \right)^2}\);
e) \({x^2} - {\left( {1 + 2x} \right)^2}\);
g) \({x^4} - 16\).
Bài 20 :
Phân tích các đa thức sau thành nhân tử:
a) \({a^2} + 12a + 36\);
b) \( - 9 + 6a - {a^2}\);
c) \(2{a^2} + 8{b^2} - 8ab\);
d) \(16{a^2} + 8a{b^2} + {b^4}\).
Bài 21 :
Phân tích các đa thức sau thành nhân tử:
a) \({x^3} - 1000\);
b) \(8{x^3} + {\left( {x - y} \right)^3}\);
c) \({\left( {x - 1} \right)^3} - 27\);
d) \({x^6} + {y^9}\).
Bài 22 :
Phân tích đa thức sau thành nhân tử: \(x^2-6x-y^2+9\)
Bài 23 :
Phân tích đa thức \(3{x^2} - 6xy + 3{y^2} - 12{z^2}\) thành nhân tử ta được
-
A.
\(3\left( {x - y - 2z} \right)\left( {x + y + 2z} \right)\)
-
B.
\(3\left( {x + y - 2z} \right)\left( {x - y + 2z} \right)\)
-
C.
\(3\left( {x - y - 2z} \right)\left( {x - y + 2z} \right)\)
-
D.
\(3\left( {x + y - 2z} \right)\left( {x + y + 2z} \right)\)
Bài 24 :
Phân tích mỗi đa thức sau thành nhân tử:
a) \(8{x^3}yz + 12{x^2}yz + 6xyz + yz;\;\;\;\)
b) \(81{x^4}\left( {{z^2} - {y^2}} \right) - {z^2} + {y^2};\)
c) \(\frac{{{x^3}}}{8} - \frac{{{y^3}}}{{27}} + \frac{x}{2} - \frac{y}{3};\;\)
d) \({x^6} + {x^4} + {x^2}{y^2} + {y^4} - {y^6}\)
Bài 25 :
Cho đa thức: \(P = {x^2} - {y^2} + 6{\rm{x}} + 9\)
a) Phân tích đa thức P thành nhân tử
b) Sử dụng kết quả của câu a để tìm thương của phép chia đa thức P cho x+y+3
Bài 26 :
Giải các phương trình sau:
a) \(5\left( {x - 3} \right) + 5 = 4x + 1\)
b) \({x^3} - 1 + \left( {1 - x} \right)\left( {x - 5} \right) = 0\)
Bài 27 :
Tính giá trị lớn nhất của biểu thức \(B = 2014 - 2{x^2} - {y^2} + 2xy - 8x + 2y\).
Bài 28 :
Phân tích đa thức thành nhân tử:
a) \({x^2} - 9\)
b) \({x^2} - 4x + 4 - {y^2}\)
Bài 29 :
Cho đa thức: \(P = {x^2} - {y^2} + 6{\rm{x}} + 9\)
a) Phân tích đa thức P thành nhân tử
b) Sử dụng kết quả của câu a để tìm thương của phép chia đa thức P cho x + y + 3


















Danh sách bình luận