Hàng ngày, hai anh em An và Bình cùng đi bộ từ nhà ở vị trí A đến trường. Trường của anh An ở vị trí B và trường của em Bình ở vị trí C theo hai hướng vuông góc với nhau (Hình 2). Anh An đi với tốc độ 4 km/h và đến trưởng sau 15 phút. Em Bình đi với tốc độ 3 km/h và đến trường sau 12 phút. Tính khoảng cách BC giữa hai trường (làm tròn kết quả đến hàng phần trăm của mét).
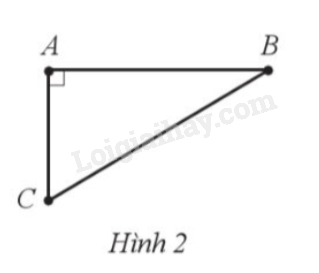
Bước 1: Áp dụng công thức \(s = v.t\) để tính quãng đường AB,AC.
Bước 2: Áp dụng định lý Pythagore trong tam giác vuông ABC để tính BC.
Đổi 15 phút = 0,25 giờ; 12 phút = 0,2 giờ.
Quãng đường AB là \(4.0,25 = 1\left( {km} \right).\)
Quãng đường AC là \(3.0,2 = 0,6\left( {km} \right).\)
Áp dụng định lý Pythagore trong tam giác vuông ABC ta có:
\(C{B^2} = A{B^2} + A{C^2} = {1^2} + 0,{6^2} = 1,36\), do đó \(CB = \sqrt {1,36} \) hay \(CB \approx 1,17\)km.
Vậy khoảng cách BC giữa hai trường khoảng 1,17km.

Các bài tập cùng chuyên đề
Bài 1 :
Sử dụng MTCT tìm căn bậc hai của \(\frac{7}{{11}}\) (làm tròn đến chữ số thập phân thứ hai) .
Bài 2 :
a) Không sử dụng MTCT, tính: \(\sqrt {{6^2}} ;\sqrt {{{\left( { - 5} \right)}^2}} ;\sqrt 5 - \sqrt {{{\left( {\sqrt 5 - 1} \right)}^2}} .\)
b) So sánh 3 với \(\sqrt {10} \) bằng hai cách:
- Sử dụng MTCT;
- Sử dụng tính chất của căn bậc hai số học đã học ở lớp 7: Nếu \(0 \le a < b\) thì \(\sqrt a < \sqrt b .\)
Bài 3 :
Tìm căn bậc hai của mỗi số sau (làm tròn đến chữ số thập phân thứ hai) :
a) 24,5;
b) \(\frac{9}{{10}}.\)
Bài 4 :
Độ dài đường kính (mét) của hình tròn có diện tích \(4\,{m^2}\) sau khi làm tròn kết quả đến chữ số thập phân thứ hai bằng
A. 2,26.
B. 2,50.
C. 1,13.
D. 1,12.
Bài 5 :
Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng \(AB = 36\;000km\), tâm quỹ đạo trùng với tâm O của Trái Đất như hình bên. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một số vị trí trên bề mặt Trái Đất. Cho biết bán kính Trái Đất khoảng 6 400km, vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh bao nhiêu kilômét? (Làm tròn kết quả đến hàng đơn vị).
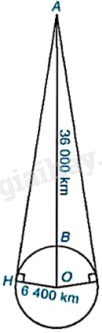
Bài 6 :
Sử dụng máy tính cầm tay, tính gần đúng các số sau (kết quả làm tròn đến chữa số thập phân thứ ba):
a) \(\sqrt {11} \)
b) \(\sqrt {7,64} \)
c) \(\sqrt {\frac{2}{3}} \)
Bài 7 :
Sử dụng máy tính cầm tay để:
a) Tìm các căn bậc hai của 10,08 (kết quả làm tròn đến chữ số thập phân thứ tư)
b) Tính giá trị của biểu thức \(\frac{{\sqrt 5 - 1}}{2}\) (kết quả làm tròn đến chữ số thập phân thứ năm)
Bài 8 :
Sử dụng máy tính cầm tay, tính (kết quả làm tròn đế chữ số thập phân thứ tư):
a) \(\sqrt {54} \)
b) \(\sqrt {24,68} \)
c) \(\sqrt 5 + \sqrt 6 + \sqrt 7 \)
Bài 9 :
Trên cần trục ở Hình 5, hai trụ a và b đứng cách nhau 20 m, hai xà ngang c và d lần lượt có độ cao 20 m và 45 m so với mặt đất. Xà chéo x có độ dài bao nhiêu mét (kết quả làm tròn đến hàng đơn vị)?

Bài 10 :
Sử dụng máy tính cầm tay, tính các căn bậc hai của:
a) \(\frac{{361}}{{144}}\);
b) 42,8 (làm tròn kết quả đến hàng phần trăm).
Bài 11 :
Sử dụng máy tính cầm tay, tính gần đúng các căn bậc hai của các số sau (làm tròn kết quả đến hàng phần nghìn):
a) 3,2;
b) 4,15.
Bài 12 :
Tải trọng an toàn m(kg) của một dây cáp thép được tính bởi công thức \(m = 8{d^2}\),
Trong đó d(mm) là đường kính của dây cáp thép.
a) Biểu diễn \({d^2}\) theo m.
b) Tìm đường kính nhỏ nhất của dây cáp thép có tải trong an toàn là 900kg (làm tròn kết quả đến hàng phần trăm).
Bài 13 :
Tính độ dài cạnh của một khu vườn hình vuông (làm tròn kết quả đến hàng phần trăm), biết diện tích của nó bằng diện tích của khu vườn hình chữ nhật có chiều rộng 5,2m và chiều dài 14m.
Bài 14 :
Sử dụng máy tính cầm tay để tìm căn bậc hai số học của các số sau (làm tròn đến chữ số thập phân thứ 2):
Bài 15 :
(Sử dụng máy tính cầm tay) Bổ sung nút bấm vào dãy nút sau để kết quả phép tính bằng 8.

-
A.

-
B.

-
C.

-
D.

Bài 16 :
Diện tích S của hình tròn bán kính r được tính theo công thức \(S = \pi {r^2}\).
a) Viết công thức tính bán kính r theo diện tích S của hình tròn.
b) Tính bán kính r (cm) của hình tròn có diện tích 20 cm2 (kết quả làm tròn đến hàng phần mười của xăngtimet).
Bài 17 :
Cho hình chữ nhật ABCD có diện tích bằng 10 cm2 và tỉ số giữa hai cạnh kề nhau AB : AD = 3:2. Tìm độ dài cạnh AB (kết quả làm tròn đến hàng phần mười của xăngtimet).
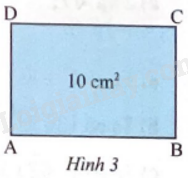
Bài 18 :
Sử dụng MTCT tính:
a) \(\sqrt {17} \) (làm tròn kết quả đến chữ số thập phân thứ ba);
b) Các căn bậc hai của 4 021 (làm tròn kết quả đến hàng phần trăm);
c) Giá trị biểu thức \(\frac{{ - 11 + \sqrt {{{11}^2} - 4.3.2} }}{{2.3}}\) (làm tròn kết quả với độ chính xác 0,005).
Bài 19 :
Tốc độ v (m/s) cần có của một vệ tinh để giữ nó chuyển động tròn ổn định trên quỹ đạo với bản kính r (m) quanh Trái Đất được cho bởi công thức \(v = \sqrt {\frac{{GM}}{r}} .\) Tính tốc độ của một vệ tinh cách tâm Trái Đất 15,92796 . 106 m, biết hằng số hấp dẫn là G = 6,67. 10-11 Nm2/kg2 và khối lượng Trái Đất là M = 5,97 . 1024 kg.
Bài 20 :
Tốc độ v (m/s) của một tàu lượn siêu tốc di chuyển trên một cung tròn bán kính r(m) được cho bởi công thức \(v = \sqrt {ar} \), trong đó a (m/s2) là gia tốc hướng tâm.
a) Nếu tàu lượn đang di chuyển với tốc độ 14 m/s và muốn đạt mức gia tốc hướng tâm tối đa là 7 m/s2 thì bán kính tối thiểu của cung tròn phải là bao nhiêu để tàu lượn không văng ra khỏi đường ray?
b) Nếu tàu lượn đang di chuyển với tốc độ 8 m/s trên cung tròn bán kính 25 m thì gia tốc hướng tâm là bao nhiêu?
Bài 21 :
Tìm căn bậc hai của mỗi số sau (làm tròn đến chữ số thập phân thứ hai):
a) 24,5.
b) \(\frac{9}{{10}}\).
Bài 22 :
Để chuẩn bị trồng cây trên vỉa hè, người ta để lại những ô đất hình tròn có diện tích khoảng \(2{m^2}\). Em hãy ước lượng (với độ chính xác 0,005) đường kính của các ô đất đó khoảng bao nhiêu mét.
Bài 23 :
Biết rằng diện tích của hình tròn lớn bằng tổng diện tích của hai hình tròn nhỏ có bán kính lần lượt là 2 cm và 3 cm. Tính bán kính r của hình tròn lớn (kết quả làm tròn đến hàng phần mười của xăngtimet).
Bài 24 :
Độ dài đường kính (mét) của hình tròn có diện tích \(4{m^2}\) sau khi làm tròn kết quả đến chữ số thập phân thứ hai bằng
A. 2,26.
B. 2,50.
C. 1,13.
D. 1,12.
Bài 25 :
Một vệ tinh địa tĩnh chuyển động theo quỹ đạo tròn cách bề mặt Trái Đất khoảng \(AB = 36\;000km\), tâm quỹ đạo trùng với tâm O của Trái Đất như hình bên. Vệ tinh phát tín hiệu vô tuyến theo đường thẳng đến một số vị trí trên bề mặt Trái Đất. Cho biết bán kính Trái Đất khoảng 6 400km, vị trí xa nhất trên bề mặt Trái Đất có thể nhận được tín hiệu từ vệ tinh cách vệ tinh bao nhiêu kilômét? (Làm tròn kết quả đến hàng đơn vị).
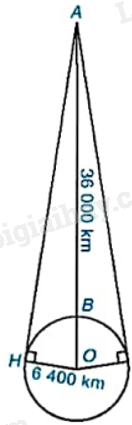
Bài 26 :
Trong quá trình lên men tinh bột thành ethanol, nấm men là chất xúc tác giúp chuyển hóa glucose thành ethanol và khí CO₂ trong điều kiện yếm khí (không có oxygen), quá trình lên men tỏa nhiệt. Từ 300 gam glucose, thực hiện quá trình lên men rượu trong phòng thí nghiệm, kết quả biểu diễn theo đồ thị sau:

Kết quả nghiên cứu nhận thấy:
- Tốc độ phản ứng tăng lên và dung dịch trở nên đặc và nhiệt độ dung dịch tăng dần.
- Sau ngày thứ 10, phản ứng hầu như dừng lại mặc dù trong dung dịch vẫn còn glucose chưa bị chuyển hóa hết.


















Danh sách bình luận