Tìm số thực x, biết:
a) \(\left| x \right| = \dfrac{{13}}{{17}}\);
b) \(\left| {x + 2,037} \right| = 0\);
c) \(\left| {x - 22} \right| = - \sqrt 3 \);
d) \(\left| x \right| = x\);
e*) \(\left| x \right| + \left| {x + 1} \right| = 0\).
Với mỗi số thực x ta có:
\(\left| x \right| = \left\{ \begin{array}{l}x{\rm{ }}(x > 0)\\x{\rm{ }}(x = 0)\\ - x{\rm{ }}(x < 0)\end{array} \right.\)
a) \(\left| x \right| = \dfrac{{13}}{{17}} \to x = \left[ \begin{array}{l}x = \dfrac{{13}}{{17}}\\x = - \dfrac{{13}}{{17}}\end{array} \right.\);
b) \(\begin{array}{l}\left| {x + 2,037} \right| = 0 \to x + 2,037 = 0\\ \to x = 0 - 2,037 = - 2,037\end{array}\);
c) \(\left| {x - 22} \right| = - \sqrt 3 \). Vì \(\left| {x - 22} \right| \ge 0\) mà \( - \sqrt 3 < 0\) nên không tồn tại giá trị nào của x thỏa mãn \(\left| {x - 22} \right| = - \sqrt 3 \).
d) \(\left| x \right| = x\) với mọi số thực x không âm. Vậy \(x \ge 0\).
e*) \(\left| x \right| + \left| {x + 1} \right| = 0\).
Ta có: \(\left\{ \begin{array}{l}\left| x \right| \ge 0\\\left| {x + 1} \right| \ge 0\end{array} \right.\) nên để \(\left| x \right| + \left| {x + 1} \right| = 0\)thì \(\left\{ \begin{array}{l}\left| x \right| = 0 \to x = 0\\\left| {x + 1} \right| = 0 \to x + 1 = 0 \to x = - 1\end{array} \right.\).
Điều này là vô lí. Vậy không có giá trị nào của x thỏa mãn \(\left| x \right| + \left| {x + 1} \right| = 0\).

Các bài tập cùng chuyên đề
Bài 1 :
Nếu \(\left| {x - 3,6} \right| = 1,4\) thì giá trị của \(x\) là:
-
A.
\(5\)
-
B.
\(5\) hoặc \(2,2\)
-
C.
\( - 5\)
-
D.
\(2,2\)
Bài 2 :
Cho x là 1 số thực bất kì, |x| là:
-
A.
Một số âm
-
B.
Một số dương
-
C.
Một số không âm
-
D.
Một số không dương
Bài 3 :
Biểu diễn các số 3 và -2 trên trục số rồi cho biết mỗi điểm ấy nằm cách gốc O bao nhiêu đơn vị.
Bài 4 :
Không vẽ hình, hãy cho biết khoảng cách của mỗi điểm sau đến gốc O: -4; -1; 0; 1; 4
Bài 5 :
Từ HĐ1 và HĐ2, hãy tìm giá trị tuyệt đối của các số 3; -2; 0; 4 và -4.
Bài 6 :
Minh viết: \(\left| { - 2,5} \right| = - 2,5\) đúng hay sai?
Bài 7 :
Tính:
a) |-2,3|;
b) |\(\dfrac{7}{5}\)|;
c) |-11|;
d) |\(-\sqrt{8}\)|
Bài 8 :
Liệt kê các phần tử của tập hợp \(A = \left\{ {x|x \in \mathbb{Z},\left| x \right| < 5} \right\}\)
Bài 9 :
Tính:
a) \(\left| { - 3,5} \right|\);
b) \(\left| {\frac{{ - 4}}{9}} \right|\);
c) \(\left| 0 \right|\);
d) \(\left| {2,0(3)} \right|.\)
Bài 10 :
Xác định dấu và giá trị tuyệt đối của mỗi số sau:
a) \(a = 1,25\);
b) \(b = - 4,1\);
c) \(c = - 1,414213562....\)
Bài 11 :
Tìm tất cả các số thực x thỏa mãn điều kiện \(\left| x \right| = 2,5\)
Bài 12 :
a) Cho hai số thực a = -1,25 và b = -2,3. So sánh a và b, |a| và |b|.
b) Ta có nhận xét trong hai số âm, số nào có giá trị tuyệt đối lớn hơn là số bé hơn.
Em hãy áp dụng nhận xét này để so sánh -12,7 và -7,12.
Bài 13 :
Cho hai số thực a = 2,1 và b = -5,2.
a) Em có nhận xét gì về hai tích a.b và -|a|.|b|?
b) Ta có cách nhân hai số khác dấu như sau: Muốn nhân hai số khác dấu ta nhân các giá trị tuyệt đối của chúng rồi đặt dấu “-“ trước kết quả.
Em hãy áp dụng quy tắc trên để tính (-2,5).3
Bài 14 :
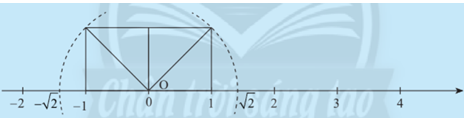
Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).
Bài 15 :
Tìm giá trị tuyệt đối của các số thực sau: \(-3,14; 41; -5; 1,(2); -\sqrt5\).
Bài 16 :
Có bao nhiêu số thực x thoả mãn |x| = \(\sqrt 3 \)?
Bài 17 :
Tìm giá trị tuyệt đối của các số sau: \( - \sqrt 7 ;\,\,\,\,\,52,\left( 1 \right);\,\,\,\,\,0,68;\,\,\,\,\,\, - \frac{3}{2};\,\,\,\,\,2\pi .\)
Bài 18 :
Sắp xếp theo thứ tự từ nhỏ đến lớn giá trị tuyệt đối của các số sau:
\( - 3,2;\,\,\,\,\,2,13;\,\,\,\, - \sqrt 2 ;\,\,\,\, - \frac{3}{7}\).
Bài 19 :
Tìm giá trị của x và y biết rằng: \(\left| x \right| = \sqrt 5 \) và \(\left| {y - 2} \right| = 0\).
Bài 20 :
Tính giá trị của biểu thức: \(M = \sqrt {\left| { - 9} \right|} \).
Bài 21 :
Tìm x, biết: \({\left( {x - 5} \right)^2} = 64\).
Bài 22 :
a) Hãy biểu diễn hai số -5 và 5 trên cùng một trục số.
b) Tính khoảng cách từ điểm 5 đến điểm 0.
c) Tính khoảng cách từ điểm -5 đến điểm 0.
Bài 23 :
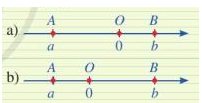
So sánh giá trị tuyệt đối của hai số thực a,b trong mỗi trường hợp sau:
Bài 24 :
Cho x = -12. Tính giá trị của mỗi biểu thức sau:
a) 18 + |x|
b) 25 - |x|
c) |3+x| - |7|
Bài 25 :
Tìm: \(\left| { - 59} \right|;\left| { - \frac{3}{7}} \right|;\left| {1,23} \right|;\left| { - \sqrt 7 } \right|\)
Bài 26 :
Chọn dấu “<”, “>”, “ =” thích hợp cho
Bài 27 :
Tính giá trị biểu thức:
a) |-137| + |-363|; b) |-28| - |98|; c) (-200) - |-25|.|3|
Bài 28 :
Tìm x, biết:
a) |x| = 4;
b) |x| = \(\sqrt 7 \);
c) |x+5| = 0;
d) \(\left| {x - \sqrt 2 } \right|\) = 0
Bài 29 :
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai?
a) Giá trị tuyệt đối của một số thực là một số dương.
b) Giá trị tuyệt đối của một số thực là một số không âm.
c) Giá trị tuyệt đối của một số thực là số đối của nó.
d) Hai số đối nhau có giá trị tuyệt đối bằng nhau.
Bài 30 :
So sánh hai số a và b trong mỗi trường hợp sau:
a) a, b là hai số dương và |a| < |b|;
b) a, b là hai số âm và |a| < |b|













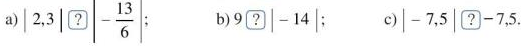





Danh sách bình luận