Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo hình chữ nhật đó bằng bao nhiêu đề xi mét (làm tròn đến hàng phần mười)?
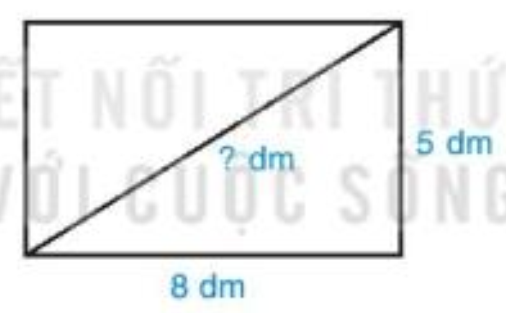
Tình tổng các bình phương độ dài hai cạnh của hình chữ nhật đó.
Vì bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó ( theo gợi ý đề bài ) và hình chữ nhật đã cho có chiều dài 8dm, chiều rộng 5dm (giả thiết) nên độ dài đường chéo là \(\sqrt {{8^2} + {5^2}} = \sqrt {89} \). Sử dụng máy tính cầm tay ta tính được \(\sqrt {89} = 9,43398...\) Làm tròn đến hàng phần mười ta được 9,4. Độ dài đường chéo hình chữ nhật là 9,4 dm.
Các bài tập cùng chuyên đề
Sử dụng máy tính cầm tay tính các căn bậc hai số học sau (làm tròn kết quả với độ chính xác 0,005, nếu cần).
\(a)\sqrt {15} ;b)\sqrt {2,56} ;c)\sqrt {17256} ;d)\sqrt {793881} \)
Kim tự tháp Kheops là công trình kiến trúc nổi tiếng thế giới. Để xây dựng được công trình này, người ta phải sử dụng tới hơn 2,5 triệu mét khối đá, với diện tích đáy lên tới 52 198,16 m2.
(Theo khoahoc.tv)
Biết rằng đáy của kim tự tháp Kheops có dạng một hình vuông. Tính độ dài cạnh đáy của kim tự tháp này (làm tròn kết quả đến chữ số thập phân thứ nhất).
Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính xác 0,005.
a) 3; b) 41; c) 2 021
Biết rằng bình phương độ dài đường chéo của một hình chữ nhật bằng tổng các bình phương độ dài hai cạnh của nó. Một hình chữ nhật có chiều dài là 8 dm và chiều rộng là 5 dm. Độ dài đường chéo của hình chữ nhật đó bằng bao nhiêu đềximét (làm tròn kết quả đến hàng phần mười)?
Sử dụng máy tính cầm tay làm tròn các số sau đến chữ số thập phân thứ nhất:
\(a = \sqrt 2 ;b = \sqrt 5 \)
Tính tổng hai số thập phân nhận được.
a) Sử dụng máy tính cầm tay bấm liên tiếp các nút
Em hãy đọc kết quả x trên màn hình rồi tính x2.
b) Sử dụng máy tính cầm tay bấm liên tiếp các nút
Em hãy đọc kết quả x trên màn hình rồi tính x2.
Dùng máy tính cầm tay để tính các căn bậc hai số học sau:
\(\sqrt 3 ;\,\sqrt {15\,\,129} ;\,\sqrt {10\,\,000} ;\,\sqrt {10} \).
Dùng máy tính cầm để:
a) Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 12 996 m2
b) Công thức tính diện tích S của hình tròn bán kính R là \(S = \pi {R^2}\). Tính bán kính của một hình tròn có diện tích là 100 cm2.
Dùng máy tính cầm tay để tính các căn bậc hai số học sau (làm tròn đến 3 chữ số thập phân).
\(a)\sqrt {2250} ;\,\,\,\,\,\,b)\sqrt {12} ;\,\,\,\,\,\,\,c)\sqrt 5 \,\,\,\,\,\,\,\,\,d)\sqrt {624} \)
Tính bán kính của một hình tròn có diện tích là 9869 m2 (dùng máy tính cầm tay).
Dùng máy tính cầm tay để tính các căn bậc hai sau (làm tròn đến 3 chữ số thập phân).
\(\begin{array}{l}a)\sqrt {133} \\b)\sqrt {99} \\c)\sqrt 7 \\d)\sqrt {1000} \end{array}\)
Sử dụng máy tính cầm tay tìm căn bậc hai số học của các số sau rồi làm tròn các kết quả với độ chính xác 0,005.
a) 3;
b) 41;
c) 2 021.
Dùng máy tính cầm tay tính và làm tròn các số sau đến hàng phần trăm: −250\(\sqrt 3 \); π\(\sqrt 2 \);\(\sqrt {13} - \sqrt 5 \)
Sử dụng máy tính cầm tay làm tròn các số sau đến chữ số thập phân thứ nhất: \(a = \sqrt 2 ;b = \sqrt 5 \). Tính tổng hai số thập phân nhận được.
