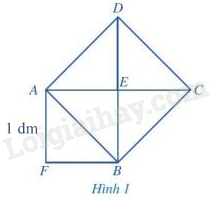
Một nền nhà có dạng hình vuông được lát bằng 289 viên gạch. Các viên gạch được lát đều có dạng hình vuông và cùng kích thước. Hai đường chéo của nền nhà được lát bằng các viên gạch màu đen, phần còn lại được lát bằng các viên gạch màu trắng (Hình 1). Tính số viên gạch màu trắng được dùng để lát nền nhà.

Muốn tính số viên gạch trắng được dùng để lát nền nhà, ta cần xác định được số viên gạch đen để lát nền nhà.
Các viên gạch được lát đều có dạng hình vuông và cùng kích thước nên số viên gạch được lát ở một cạnh của nền nhà là:
\(\sqrt {289} = 17\) (viên gạch).
Hai đường chéo của nền nhà được lát bằng các viên gạch màu đen và hai đường chéo có chung nhau 1 viên gạch nên số viên gạch màu đen được dùng để lát nền nhà là:
\(17{\rm{ }}{\rm{. 2 }} - {\rm{ 1 = 33}}\) (viên gạch).
Vậy số viên gạch màu trắng dùng để lát nền nhà là:
\(289 - 33 = 256\) (viên gạch).

Các bài tập cùng chuyên đề
Bài 1 :
Tính độ dài cạnh của hình vuông có diện tích là 0,49 ha.
-
A.
49 m
-
B.
0,7 km
-
C.
70 m
-
D.
24,01 m
Bài 2 :
Tính:
a) \(\sqrt {16}\);
b) \(\sqrt {81}\);
c) \(\sqrt {{{2021}^2}}\).
Bài 3 :
Sàn thi đấu bộ môn cử tạ có dạng một hình vuông, diện tích 144 m2. Em hãy tính chu vi của sàn thi đấu đó
Bài 4 :
Cho biết \({153^2} = 23409\). Hãy tính \(\sqrt {23409} \)
Bài 5 :
Từ các số là bình phương của 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:
a) 9;
b) 16;
c) 81;
d) 121
Bài 6 :
Khi tìm căn bậc hai số học của một số tự nhiên ta thường phân tích số đó ra thừa số nguyên tố. Chẳng hạn:
Vì \(324 = {2^2}{.3^4} = {({2.3^2})^2} = {18^2}\) nên \(\sqrt {324} = 18\)
Tính căn bậc hai số học của 129 600.
Bài 7 :
Tính độ dài các cạnh của hình vuông có diện tích bằng:
a) 81 dm2; b) 3 600 m2; c) 1 ha
Bài 8 :
Để lát một mảnh sân hình vuông có diện tích 100 m2, người ta cần dùng bao nhiêu viên gạch hình vuông có cạnh dài 50 cm (coi các mạch ghép là không đáng kể)?
Bài 9 :
Tính:
a) \(\sqrt{1}\)
b) \(\sqrt{1+2+1}\)
c) \(\sqrt{1+2+3+2+1}\)
Bài 10 :
Tính:
a) \((\sqrt {3})^2\)
b) \((\sqrt {21})^2\)
Bài 11 :
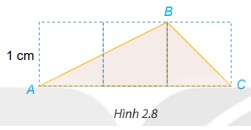
Dùng thước dây có vạch chia để đo độ dài đường gấp khúc ABC trong Hình 2.8 (đơn vị xentimet, làm tròn đến chữ số thập phân thứ nhất). So sánh kết quả với kết quả với kết quả của Bài tập 2.27.
Bài 12 :
a) Tìm giá trị của x2 với x lần lượt bằng 2; 3; 4; 5; 10.
b) Tìm số thực không âm x với x2 lần lượt bằng 4; 9; 16; 25; 100.
Bài 13 :
Viết các căn bậc hai số học của: 16; 7; 10; 36.
Bài 14 :
Tính độ dài cạnh của một mảnh đất hình vuông có diện tích là 169 m2.
Bài 15 :
Tính:
\(a)\sqrt {64} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,b)\sqrt {{{25}^2}} ;\,\,\,\,\,\,\,\,\,\,\,c)\sqrt {{{\left( { - 5} \right)}^2}} .\)
Bài 16 :
Hãy thay dấu ? bằng các số thích hợp.
Bài 17 :
Bác Thu thuê thợ lát gạch một cái sân hình vuông hết tất cả là 10 125 000 đồng. Cho biết chi phí cho 1 m2 (kể cả công thợ và vật liệu) là 125 000 đồng. Hãy tính chiều dài cạnh của cái sân.
Bài 18 :
Tính:
\(\sqrt {91} ;\,\,\,\sqrt {49} ;\,\,\,\,\sqrt {{{12}^2}} ;\,\,\,\sqrt {{{\left( { - 4} \right)}^2}} \).
Bài 19 :
Tính: \(a){3^2};b){(0,4)^2}\)
Bài 20 :
Tìm giá trị của:
\(\begin{array}{l}a)\sqrt {1600} ;\\b)\sqrt {0,16} ;\\c)\sqrt {2\frac{1}{4}} \end{array}\)
Bài 21 :
a) Đọc các số sau: \(\sqrt {15} ;\sqrt {27,6} ;\sqrt {0,82} \)
b) Viết các số sau: căn bậc hai số học của 39; căn bậc hai số học của \(\frac{9}{{11}}\); căn bậc hai số học của \(\frac{{89}}{{27}}\)
Bài 22 :
Chứng tỏ rằng:
a) Số 0,8 là căn bậc hai số học của số 0,64
b) Số -11 không phải là căn bậc hai số học của số 121
c) Số 1,4 là căn bậc hai số học của số 1,96 nhưng –1,4 không phải là căn bậc hai số học của số 1,96.
Bài 23 :
Tìm số thích hợp cho
Bài 24 :
Tính giá trị của biểu thức:
a) \(\sqrt {0,49} + \sqrt {0,64}\)
b) \(\sqrt {0,36} - \sqrt {0,81}\)
c) \(8.\sqrt 9 - \sqrt {64}\)
d) \(0,1.\sqrt {400} + 0,2.\sqrt {1600}\)
Bài 25 :
Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 dm, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.
a) Tính diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
Bài 26 :
Tính:
\(\begin{array}{l}a)2.\sqrt 6 .( - \sqrt 6 );\\b)\sqrt {1,44} - 2.{(\sqrt {0,6} )^2};\\c)0,1.{(\sqrt 7 )^2} + \sqrt {1,69} ;\\d)( - 0,1).{(\sqrt {120} )^2} - \frac{1}{4}.{(\sqrt {20} )^2}\end{array}\)
Bài 27 :
Tìm số x không âm, biết:
\(\begin{array}{l}a)\sqrt x - 16 = 0;\\b)2\sqrt x = 1,5;\\c)\sqrt {x + 4} - 0,6 = 2,4\end{array}\)
Bài 28 :
a) Đọc các số sau: \(\sqrt {35} \); \(\sqrt {1,96} \); \(\sqrt {\dfrac{1}{{225}}} \).
b) Viết các số sau: căn bậc hai số học của 2,4; căn bậc hai số học của 3,648; căn bậc hai số học của \(\dfrac{{49}}{{1{\rm{ }}089}}\).
Bài 29 :
Trong các cách viết sau, cách viết nào đúng? Vì sao?
a) \(\sqrt {81} = \pm {\rm{ }}9\).
b) \(\sqrt {81} = - {\rm{ }}9\).
c) \(\sqrt {81} = 9\) .
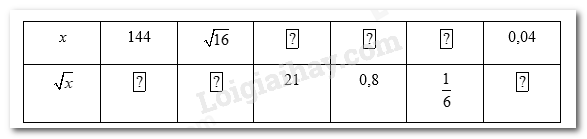
Bài 30 :
Tìm số thích hợp cho ?




















Danh sách bình luận