a) Lập bảng giá trị của \(2^n\) với n ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10};
b) Viết dưới dạng lũy thừa của 2 các số sau: 8; 256; 1 024; 2 048.
+Quy ước: \(a^0=1\)
Tính các giá trị của \(2^n\) với n ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
a)
+) Với n = 0 thì \(2^n= 2^0 = 1\)
+) Với n = 1 thì \(2^n = 2^1 = 2\)
+) Với n = 2 thì \(2^n = 2^2=2.2 = 4\)
+) Với n = 3 thì \(2^n = 2^3=2.2.2 = 8\)
+) Với n = 4 thì \(2^n = 2^4=2.2.2.2 = 16\)
+) Với n = 5 thì \(2^n = 2^5=2.2.2.2.2 = 32\)
+) Với n = 6 thì \(2^n = 2^6=2.2.2.2.2.2 = 64\)
+) Với n = 7 thì \(2^n = 2^7=2.2.2.2.2.2.2 = 128\)
+) Với n = 8 thì \(2^n = 2^8=2.2.2.2.2.2.2.2 = 256\)
+) Với n = 9 thì \(2^n = 2^9=2.2.2.2.2.2.2.2.2 = 512\)
+) Với n = 10 thì \(2^n = 2^{10}=2.2.2.2.2.2.2.2.2.2 = 1024\)
Ta có bảng sau:
b) Từ bảng trên ta thấy:
\(\begin{array}{l}8 = {2^3};256 = {2^8};1024 = {2^{10}};\\2048 = 1024.2 = {2^{10}}{.2^1} = {2^{10 + 1}} = {2^{11}}\end{array}\)
Lời giải hay

Các bài tập cùng chuyên đề
Bài 1 :
Số tự nhiên \(m\) nào dưới đây thỏa mãn \({20^{2018}} < {20^m} < {20^{2020}}?\)
-
A.
\(m = 2020\)
-
B.
\(m = 2018\)
-
C.
\(m = 2019\)
-
D.
\(m = 20\)
Bài 2 :
Tổng các số tự nhiên thỏa mãn \({\left( {x - 4} \right)^5} = {\left( {x - 4} \right)^3}\) là
-
A.
\(8\)
-
B.
\(4\)
-
C.
\(5\)
-
D.
\(9\)
Bài 3 :
So sánh \({16^{19}}\) và \({8^{25}}\) .
-
A.
\({16^{19}} < {8^{25}}.\)
-
B.
\({16^{19}} > {8^{25}}.\)
-
C.
\({16^{19}} = {8^{25}}.\)
-
D.
Không đủ điều kiện so sánh.
Bài 4 :
Tìm $x$ biết: \(65 - {4^{x + 2}} = 1\)
-
A.
$5$
-
B.
$4$
-
C.
$3$
-
D.
$1$
Bài 5 :
Có bao nhiêu số tự nhiên \(m\) thỏa mãn \({20^{2018}} \le {20^{m + 1}} < {20^{2022}}?\)
-
A.
\(1\)
-
B.
\(5\)
-
C.
\(4\)
-
D.
\(3\)
Bài 6 :
Có bao nhiêu số tự nhiên thỏa mãn \({\left( {2x - 6} \right)^7} = {\left( {2x - 6} \right)^9}\)?
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(5\)
-
D.
\(3\)
Bài 7 :
So sánh \({27^{11}}\) và \({81^8}\).
-
A.
\({27^{11}} < {81^8}\)
-
B.
\({27^{11}} > {81^8}\)
-
C.
\({27^{11}} = {81^8}\)
-
D.
Không đủ điều kiện so sánh
Bài 8 :
Viết các tích sau dưới dạng một luỹ thừa:
a) 9.9.9.9.9; b) 10. 10. 10. 10.
c) 5.5.5.25 d) a.a.a.a.a.a
Bài 9 :
Hoàn thành bằng sau vào vở
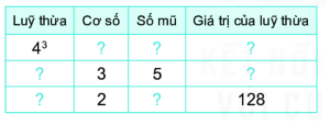
Bài 10 :
Tính
a) 25; b) 33; c) 52; d) 109.
Bài 11 :
Viết các số sau thành tổng giá trị các chữ số của nó bằng cách dùng các luỹ thừa của 10:
215; 902; 2020; 883 001.
Bài 12 :
Tính 112, 1112. Từ đó hãy dự đoán kết quả của 1 1112.
Bài 13 :
Ta có: 1 + 3 + 5 = 9 = 32.
Viết các tổng sau dưới dạng bình phương của một số tự nhiên
a) 1 + 3 + 5 + 7; b) 1 + 3 + 5 + 7 + 9.
Bài 14 :
Bảng sau đây chỉ ra cách tính số hạt thóc ở một số ô trong bàn cờ trong bài toán mở đầu:
Để tìm số hạt thóc ở ô thứ 8, ta phải thực hiện phép nhân có bao nhiêu thừa số 7.
Bài 15 :
Hoàn thành bảng bình phương của các số tự nhiên từ 1 đến 10.

Bài 16 :
1) Tính số hạt thóc có trong ô thứ 7 của bàn cờ nói trong bài toán mở đầu.
2) Hãy viết mỗi số tự nhiên sau thành tổng giá trị các chữ số của nó bằng cách dùng các luỹ thừa của 10 theo mẫu:
4 257 = 4 . 103 +2. 102 + 5.10 + 7.
a) 23 197
b) 203 184.
Bài 17 :
Lũy thừa của \(3^4\) sẽ bằng?
-
A.
9
-
B.
27
-
C.
81
-
D.
243
Bài 18 :
Theo Tổng cục Thống kê, tháng 10 năm 2020 dân số Việt Nam được làm tròn là 98000000 người.
Em hãy viết dân số Việt Nam dưới dạng tích của một số với một luỹ thừa của 10.
Bài 19 :
Thực vật được cấu tạo bởi các tế bào. Tế bào lớn lên đến một kích thước nhất định thì phân chia ra thành 2 tế bào con. Các tế bào con tiếp tục tăng kích thước và lại phân chia thành 4 tế bào, rồi thành 8 tế bào, ...
Hãy cho biết số tế bào con có được sau lần phân chia thứ tư, thứ năm, thứ sáu từ một tế bào ban đầu.
Bài 20 :
Viết gọn các tích sau bằng cách dùng lũy thừa.
a) 5.5.5
b) 7.7.7.7.7.7
Bài 21 :
a) Viết các tích sau dưới dạng lũy thừa: 3.3.3; 6.6.6.6.
b) Phát biểu hoàn thiện các câu sau:
\({3^2}\) còn gọi là “3…” hay “…của 3”; \({5^3}\) còn gọi là “5…” hay “…của 5”.
c) Hãy đọc các lũy thừa sau và chỉ rõ cơ số, số mũ: \({3^{10}}\); \({10^5}\).
Bài 22 :
Vi khuẩn E.coli trong điều kiện nuôi cấy thích hợp cứ 20 phút lại phân đôi một lần. Giả sử lúc đầu có 1 vi khuẩn. Sau 120 phút có bao nhiêu vi khuẩn?
Bài 23 :
Viết các tích sau dưới dạng lũy thừa:
a) \(5.5.5.5\)
b) 9.9.9.9.9.9.9
c) 7.7.7.7.7
d) \(a.a.a.a.a.a.a.a\)
Bài 24 :
Xác định cơ số, số mũ và tính mỗi lũy thừa sau: \({2^5},{5^2},{9^2},{1^{10}},{10^1}\).
Bài 25 :
Viết các số sau dưới dạng lũy thừa với cơ số cho trước.
a) 81, cơ số 3;
b) 81, cơ số 9;
c) 64, cơ số 2;
d) 100 000 000, cơ số 10.
Bài 26 :
Cho biết \({11^2} = 121;{111^2} = 12321\). Hãy dự đoán \({1111^2}\) bằng bao nhiêu. Kiểm tra lại dự đoán đó.
Bài 27 :
Viết và tính các lũy thừa sau:
a) Năm mũ hai;
b) Hai lũy thừa bảy;
c) Lũy thừa bậc ba của sáu.
Bài 28 :
Viết các số sau dưới dạng lũy thừa với cơ số cho trước:
a) 25 cơ số 5;
b) 64 cơ số 4.
Bài 29 :
Lũy thừa của \(10^3\) bằng:
-
A.
10
-
B.
30
-
C.
100
-
D.
1000
Bài 30 :
Các số 4; 8; 9; 16; 27; 64; 81; 125; 225 là bình phương hay lập phương của những số nào?



















Danh sách bình luận