Chứng tỏ rằng \(\sqrt 2 \) là số vô tỉ.
Ta chứng minh \(\sqrt 2 \) là số vô tỉ bằng cách chứng minh điều ngược lại là sai: giả sử \(\sqrt 2 \) không là số vô tỉ.
Giả sử \(\sqrt 2 \) là số hữu tỉ.
Như vậy, \(\sqrt 2 \) có thể viết được dưới dạng \(\dfrac{m}{n}\) với \(m,n \in \mathbb{N}\) và \((m,n) = 1\).
Ta có: \(\sqrt 2 = \dfrac{m}{n}\) nên \({\left( {\sqrt 2 } \right)^2} = {\left( {\dfrac{m}{n}} \right)^2}\) hay \(2 = \dfrac{{{m^2}}}{{{n^2}}}\). Suy ra: \({m^2} = 2{n^2}\).
Mà \((m,n) = 1\) nên \({m^2}\) chia hết cho 2 hay m chia hết cho 2. Do đó \(m = 2k\) với \(k \in \mathbb{N}\) và \((k,n) = 1\).
Thay \(m = 2k\) vào \({m^2} = 2{n^2}\) ta được: \(4{k^2} = 2{n^2}\) hay \({n^2} = 2{k^2}\).
Do \((k,n) = 1\) nên \({n^2}\) chia hết cho 2 hay n chia hết cho 2.
Suy ra m và n đều chia hết cho 2 mâu thuẫn với \((m,n) = 1\).
Vậy \(\sqrt 2 \) không là số hữu tỉ mà là số vô tỉ.

Các bài tập cùng chuyên đề
Bài 1 :
Số nào sau đây là 1 số vô tỉ?
-
A.
0
-
B.
Căn bậc hai số học của 15
-
C.
Căn bậc hai số học của 16
-
D.
Căn bậc hai số học của 0,25
Bài 2 :
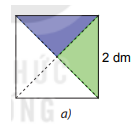
Cắt một hình vuông cạnh bằng 2 dm, rồi cắt nó thành bốn tam giác vuông bằng nhau dọc theo hai đường chéo của hình vuông (H.2.2.a)
Bài 3 :
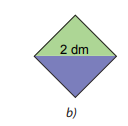
Lấy hai trong bốn tam giác nhận được ở trên ghép thành một hình vuông (H.2.2.b). Em hãy tính diện tích hình vuông nhận được.
Bài 4 :
Dùng thước có vạch chia để đo độ dài cạnh hình vuông nhận được trong HĐ2. Độ dài cạnh hình vuông này bằng bao nhiêu đềximét ?
Bài 5 :
Người xưa đã tính đường kính thân cây theo quy tắc “quân bát, phát tam, tồn ngũ, quân nhị”, tức là lấy chu vi thân cây chia làm 8 phần bằng nhau (quân bát); bớt đi ba phần (phát tam) còn lại 5 phần (tồn ngũ) rồi chia đôi kết quả (quân nhị). Hãy cho biết người xưa đã ước lượng số \(\pi \) bằng bao nhiêu?
Bài 6 :
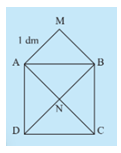
Cho hai hình vuông ABCD và AMBN như hình bên. Cho biết cạnh AM=1 dm.
- Em hãy cho biết diện tích hình vuông ABCD gấp mấy lần diện tích hình vuông AMBN.
- Tính diện tích hình vuông ABCD.
- Hãy biểu diễn diện tích hình vuông ABCD theo độ dài đoạn AB.
Bài 7 :
Hoàn thành các phát biểu sau:
a) Số a=5,123 là một số thập phân hữu hạn nên a là số .?.
b) Số b = 6,15555... = 6,1(5) là một số thập phân vô hạn tuần hoàn nên b là số .?.
c) Người ta chứng minh được \(\pi= 3,14159265...\) là một số thập phân vô hạn không tuần hoàn. Vậy \(\pi\) là số ?.
d) Cho biết số c=2,23606... là một số thập phân vô hạn không tuần hoàn. Vậy c là số .?.
Bài 8 :
Viết số hữu tỉ \(\frac{1}{3}\) dưới dạng số thập phân vô hạn tuần hoàn
Bài 9 :
Phát biểu "Mỗi số vô tỉ đều không thể là số hữu tỉ” đúng hay sai? Vì sao?
Bài 10 :
Tìm những số vô tỉ trong các số sau đây:
-6,123(456);\( - \sqrt 4 ;\sqrt {\frac{4}{9}} ;\sqrt {11}; \sqrt{15}\)
Bài 11 :
-
A.
\(\mathbb{Z}\)
-
B.
\(\mathbb{I}\)
-
C.
\(\mathbb{Q}\)
-
D.
\(\mathbb{N}\)
Bài 12 :
Số nào sau đây là số thập phân vô hạn không tuần hoàn?
-
A.
–1,23;
-
B.
\(\frac{1}{2}\);
-
C.
3,(45);
-
D.
\(\sqrt 2\).
Bài 13 :
Trong các tập hợp sau, tập hợp nào có tất cả các thành phần tử đều là số vô tỉ?
a) \(A = \left\{ { - {\rm{ }}0,1;{\rm{ }}\sqrt {12} ;\dfrac{{21}}{{32}};{\rm{ }} - {\rm{ 316}}} \right\}\);
b) \(B = \left\{ {32,1;{\rm{ }}\sqrt {25} ;{\rm{ }}\sqrt {\dfrac{1}{{16}}} ;{\rm{ }}\sqrt {0,01} } \right\}\);
c) \(C = \left\{ {\sqrt 3 ;{\rm{ }}\sqrt 5 ;{\rm{ }}\sqrt {31} ;{\rm{ }}\sqrt {83} } \right\}\);
d) \(D = \left\{ { - \dfrac{1}{3};{\rm{ }}\dfrac{{231}}{2};{\rm{ }}\dfrac{2}{5};{\rm{ }} - {\rm{3}}} \right\}\).
Bài 14 :
Số nào trong các số: \( - \dfrac{{16}}{3};\sqrt {36} ;\sqrt {47} ; - 2\pi ;\sqrt {0,01} ;2 + \sqrt 7 \) là số vô tỉ?
Bài 15 :
Số nào trong các số sau là số vô tỉ?
\(a = 0,7777...\); \(b = 0,70700700070000....\); \(c = \dfrac{{ - 1}}{7}\); \(d = \sqrt {{{\left( { - 7} \right)}^2}} \)
Bài 16 :
Chọn phát biểu đúng trong các phát biểu sau:
a) \(\sqrt 3 \) ∈ I
b) \(\sqrt {25} \) ∈ I
c) \(-\pi \in I\)
d) \(\sqrt {\dfrac{{100}}{{47}}} \) ∈ Q
Bài 17 :
Nếu \(a,b \in I\) thì
A. \(a + b \in I\)
B. \(a.b \in I\)
C. \(a:b \in I\)
D. \(a + 1 \in I\).
Bài 18 :
Trong các khẳng định sai, khẳng định nào đúng?
A.Tích của hai số vô tỉ là một số vô tỉ;
B. Tổng của hai số vô tỉ là một số vô tỉ;
C. Tổng của một số hữu tỉ và một số vô tỉ là một số vô tỉ.
D. Thương của hai số vô tỉ là một số vô tỉ.
Bài 19 :
Tích của một số vô tỉ với một số nguyên dương là số hữu tỉ hay vô tỉ? Hãy giải thích tại sao có vô số số vô tỉ.
Bài 20 :
Trong các kết luận sau đây, kết luận nào đúng, kết luận nào sai?
a) Tổng của hai số vô tỉ là một số vô tỉ.
b) Tổng của hai số vô tỉ dương là một số vô tỉ.
c) Tổng của hai số vô tỉ âm là một số vô tỉ.
Bài 21 :
Tìm số vô tỉ trong các số sau: \(\sqrt 2 \);-\(\sqrt 4 \);\(\sqrt {\dfrac{{16}}{9}} \)
Bài 22 :
Trong các số sau, số nào là số vô tỉ:
\(34,(3);{\rm{ }}5,234561213141516...;{\rm{ }} - 45,8(89);{\rm{ }} - \sqrt {121} ;{\rm{ }}\sqrt {19} ;{\rm{ }}\sqrt {\dfrac{{25}}{{16}}} \).
Bài 23 :
Cho \(\sqrt {99} = 9,94987471...\) và \(b = 5,(123)\). Hai số \(a; b\) là số thập phân hữu hạn, số thập phân vô hạn tuần hoàn hay số vô tỉ? Tìm chữ số thập phân thứ năm của số \(b\).
Bài 24 :
Trong các số sau, số nào là số vô tỉ?
-
A.
0,23;
-
B.
1,234567…;
-
C.
1,33333…;
-
D.
0,5.
Bài 25 :
Nhận xét đúng về căn bậc hai số học của 7 là:
-
A.
một số hữu tỉ;
-
B.
một số tự nhiên;
-
C.
một số nguyên dương;
-
D.
một số vô tỉ.
Bài 26 :
Trong các số sau, số nào là số vô tỉ?
-
A.
\(\sqrt {{5^2}} \).
-
B.
\(\sqrt 3 \).
-
C.
\(\sqrt {{{\left( {3,5} \right)}^2}} \).
-
D.
\(\sqrt {16} \).
Bài 27 :
Trong các số sau, số nào là số vô tỉ?
-
A.
\(\sqrt 3 \).
-
B.
\(\frac{{ - 13}}{9}\).
-
C.
\(0\).
-
D.
\(2023\).
Bài 28 :
Số nào là số vô tỉ trong các số sau:
-
A.
\(\frac{5}{6}\).
-
B.
\( - \sqrt 5 \).
-
C.
\(0\).
-
D.
\(6,5\).
Bài 29 :
Trong các số sau đây, số nào là số vô tỉ?
-
A.
\(\sqrt {25} \).
-
B.
\(\sqrt {16} \).
-
C.
\(\sqrt {17} \).
-
D.
\(\sqrt 9 \).
Bài 30 :
Tập hợp các số vô tỉ được kí hiệu làA. \(\mathbb{Z}\).
B. \(I\).
C. \(\mathbb{Q}\).
D. \(\mathbb{R}\).


















Danh sách bình luận