Sắp xếp các số sau theo thứ tự tăng dần: \(\sqrt {\dfrac{1}{{16}}} ;{\rm{ }}4\dfrac{1}{7};{\rm{ }}1,(3);{\rm{ }}\sqrt {81} ;{\rm{ }} - \sqrt {25} ;{\rm{ }} - 12,1\).
Ta so sánh các số với nhau để sắp xếp các số theo thứ tự tăng dần.
Ta có: \( - \sqrt {25} ;{\rm{ }} - 12,1 < 0 < \sqrt {\dfrac{1}{{16}}} ;{\rm{ }}4\dfrac{1}{7};{\rm{ }}1,(3);{\rm{ }}\sqrt {81} \).
Xét \( - \sqrt {25} ;{\rm{ }} - 12,1\): \( - \sqrt {25} = - {\rm{ }}5 > - 12,1\) nên \( - \sqrt {25} {\rm{ > }} - 12,1\).
Xét \(\sqrt {\dfrac{1}{{16}}} ;{\rm{ }}4\dfrac{1}{7};{\rm{ }}1,(3);{\rm{ }}\sqrt {81} \):
\(\begin{array}{l}\sqrt {\dfrac{1}{{16}}} = \dfrac{1}{4} = 0,25\\4\dfrac{1}{7} = \dfrac{{29}}{7} = 4,(142857)\\\sqrt {81} = 9\end{array}\)
Mà \(0,25 < 1,(3) < 4,(142857) < 9\) nên: \(\sqrt {\dfrac{1}{{16}}} < 1,(3) < 4\dfrac{1}{7} < \sqrt {81} \).
Vậy các số theo thứ tự tăng dần là: \( - 12,1;{\rm{ }} - \sqrt {25} ;{\rm{ }}\sqrt {\dfrac{1}{{16}}} ;{\rm{ }}1,(3);{\rm{ }}4\dfrac{1}{7};{\rm{ }}\sqrt {81} \).

Các bài tập cùng chuyên đề
Bài 1 :
Thay dấu “?” bằng chữ số thích hợp.
Bài 2 :
So sánh:
a) 12,26 và 12,(24);
b) 31,3(5) và 29,9(8)
Bài 3 :
Chọn phát biểu đúng trong các phát biểu sau:
\(a)\sqrt 2 \in I;\,\,\,\,\,b)\sqrt 9 \in I;\,\,\,\,c)\,\pi \in I;\,\,\,\,\,d)\sqrt 4 \in \mathbb{Q}\)
Bài 4 :

Bài 5 :
Chữ số thập phân thứ 221 sau dấu “,” của số hữu tỉ \(\dfrac{1}{7}\) được viết dưới dạng số thập phân vô hạn tuần hoàn là chữ số nào?
Bài 6 :
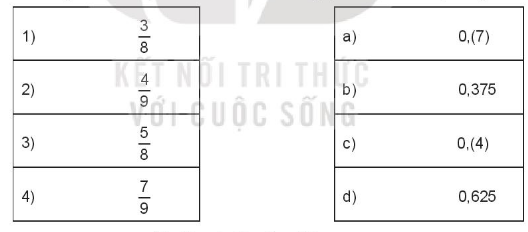
Nối mỗi phân số ở cột bên trái với cách viết thập phân của nó ở cột bên phải:
Bài 7 :
Trong các số thập phân sau, số nào là số thập phân hữu hạn? Số nào là số thập phân vô hạn tuần hoàn ?
0,1 ; -1,(23); 11,2(3); -6,725.
Bài 8 :
So sánh
a) 12,26 và 12,(24)
b) 31,3(5) và 29,9(8)
Bài 9 :
So sánh:
a) \(213,6(42)\) và \(213,598...\);
b) \( - 43,001\) và \( - 43,(001)\);
c) \( - \sqrt {237} \) và \( - 15\);
d) \(\sqrt {1\dfrac{{40}}{{81}}} \) và \(\sqrt {1\dfrac{{20}}{{101}}} \);
e) \(2 + \sqrt {37} \) và \(6 + \sqrt 2 \);
g) \(\dfrac{{\sqrt {{5^2}} + \sqrt {{{15}^2}} }}{{\sqrt {{4^2}} + \sqrt {{{36}^2}} }}\) và \(\dfrac{1}{{\sqrt {{2^2}} }}\).
Bài 10 :
Sắp xếp các số sau theo thứ tự tăng dần:
a) \( - 0,34;{\rm{ }} - 6,(25);{\rm{ }}1\dfrac{5}{9};{\rm{ }}\sqrt {169} ;{\rm{ }}\sqrt {15} \);
b) \(1,0(09);{\rm{ }}\sqrt {64} ;{\rm{ }}31\dfrac{1}{5};{\rm{ }} - 34,(5);{\rm{ }} - \sqrt {225} \).
Bài 11 :
Sắp xếp các số sau theo thứ tự giảm dần:
a) \(2\dfrac{1}{4};{\rm{ }}\sqrt {16} ;{\rm{ }} - \sqrt {83} ;{\rm{ }} - \sqrt {196} ;{\rm{ }} - 0,0(51);\)
b) \(21\dfrac{1}{6};{\rm{ }}\sqrt {49} ;{\rm{ }} - \sqrt {144} ;{\rm{ }} - 614,1;{\rm{ }} - 111,0(3).\)













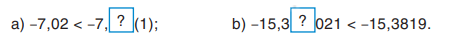





Danh sách bình luận