Một vật rơi từ do từ độ cao so với mặt đất là 78,4 mét. Bỏ qua sức cản không khí, quãng đường chuyển động s (mét) của vật rơi tự do sau thời gian t được biểu diễn gần đúng bởi công thức \(s = 4,9{t^2}\), trong đó t là thời gian tính bằng giây. Sau bao lâu kể từ khi bắt đầu rơi thì vật này chạm mặt đất? (Làm tròn kết quả đến chữ số hàng phần mười).
+ Dựa vào đề bài lập phương trình.
+ Đua phương trình vừa lập về dạng phương trình tích \(\left( {at + b} \right)\left( {ct + d} \right) = 0\).
+ Để giải phương trình tích \(\left( {at + b} \right)\left( {ct + d} \right) = 0\), ta giải hai phương trình \(at + b = 0\) và \(ct + d = 0\).
+ Kết hợp với điều kiện của t và đưa ra kết luận.
Thời gian t (giây) \(\left( {t > 0} \right)\) để vật chạm đất là nghiệm của phương trình
\(4,9{t^2} = 78,4\)
\({t^2} = 78,4:4,9\)
\({t^2} = 16\)
\(\left( {t - 4} \right)\left( {t + 4} \right) = 0\)
\(t = 4\) (giây)
Vậy sau 4 giây kể từ khi bắt đầu rơi thì vật này chạm mặt đất.
Các bài tập cùng chuyên đề
Chọn khẳng định đúng.
Tích các nghiệm của phương trình \({x^3} + 4{x^2} + x - 6 = 0\) là
Nghiệm lớn nhất của phương trình \(\left( {{x^2} - 1} \right)\left( {2x - 1} \right) = \left( {{x^2} - 1} \right)\left( {x + 3} \right)\) là
Nghiệm nhỏ nhất của phương trình \({\left( {2x + 1} \right)^2} = {\left( {x - 1} \right)^2}\) là
Tập nghiệm của phương trình \(\left( {{x^2} + x} \right)\left( {{x^2} + x + 1} \right) = 6\) là
Tìm m để phương trình \(\left( {2m - 5} \right)x - 2{m^2} + 8 = 43\) có nghiệm \(x = - 7\).
Tập nghiệm của phương trình
\({\left( {5{x^2} - 2x + 10} \right)^2} = {\left( {3{x^2} + 10x - 8} \right)^2}\) là:
Biết rằng phương trình \({\left( {{x^2} - 1} \right)^2} = 4x + 1\) có nghiệm lớn nhất là \({x_0}\) . Chọn hẳng định đúng.
Cho phương trình $\left( 1 \right):$ \(x\left( {{x^2} - 4x + 5} \right) = 0\) và phương trình \(\left( 2 \right):\) \(\left( {{x^2} - 1} \right)\left( {{x^2} + 4x + 5} \right) = 0\).
Chọn khẳng định đúng.
Phương trình \({x^2} + x = 0\) có số nghiệm là
Phương trình \(2x + k = x - 1\) nhận \(x = 2\) là nghiệm khi
Giải phương trình: \(2x\left( {x - 5} \right) + 21 = x\left( {2x + 1} \right) - 12\) ta được nghiệm \({x_0}.\) Chọn câu đúng.
Số nghiệm của phương trình \(\left( {x + 2} \right)\left( {{x^2} - 3x + 5} \right) = \left( {x + 2} \right){x^2}\) là
Cho phương trình: \(\left( {4{m^2} - 9} \right)x = 2{m^2} + m - 3\) . Tìm m để phương trình có vô số nghiệm
Cho phương trình \(5 - 6\left( {2x - 3} \right) = x\left( {3 - 2x} \right) + 5\). Chọn khẳng định đúng.
Tích các nghiệm của phương trình \({x^3} - 3{x^2} - x + 3 = 0\) là
Số nghiệm của phương trình \(\left( {{x^2} + 9} \right)\left( {x - 1} \right) = \left( {{x^2} + 9} \right)\left( {x + 3} \right)\) là
Nghiệm nhỏ nhất của phương trình \({\left( { - \dfrac{1}{2}x + 1} \right)^2} = {\left( {\dfrac{3}{2}x - 1} \right)^2}\) là
Tập nghiệm của phương trình \(\left( {{x^2} - x - 1} \right)\left( {{x^2} - x + 1} \right) = 3\) là
Tìm \(m\) để phương trình \(\left( {2m - 5} \right)x - 2{m^2} - 7 = 0\) nhận \(x = - 3\) làm nghiệm.
Số nghiệm của phương trình \({\left( {5{x^2} - 2x + 10} \right)^3} = {\left( {3{x^2} + 10x - 6} \right)^3}\) là:
Biết rằng phương trình \({\left( {4{x^2} - 1} \right)^2} = 8x + 1\) có nghiệm lớn nhất là \({x_0}\). Chọn khẳng định đúng.
Cho phương trình \({x^4} - 8{x^2} + 16 = 0\). Chọn khẳng định đúng.
Giải các phương trình sau:
a) \(\left( {3x + 1} \right)\left( {2 - 4x} \right) = 0;\)
b) \({x^2} - 3x = 2x - 6.\)
Giải bài toán ở tình huống mở đầu.
Tình huống mở đầu: Trong một khu vườn hình vuông có cạnh bằng 15m người ta làm một lối đi xung quanh vườn có bề rộng là x (m) (H.2.1). Để diện tích phần đất còn lại là \(169{m^2}\) thì bề rộng x của lối đi là bao nhiêu?
Giải các phương trình sau:
a) \(\left( {{x^2} - 4} \right) + x\left( {x - 2} \right) = 0;\)
b) \({\left( {2x + 1} \right)^2} - 9{x^2} = 0.\)
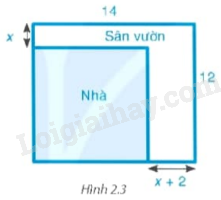
Bác An có một mảnh đất hình chữ nhật với chiều dài 14m và chiều rộng 12m. Bác dự định xây nhà trên mảnh đất đó và dành một phần diện tích đất để làm sân vườn như hình 2.3. Biết diện tích đất làm nhà là \(100{m^2}.\) Hỏi x bằng bao nhiêu mét?
Giải các phương trình sau:
a) \(2\left( {x + 1} \right) = \left( {5x - 1} \right)\left( {x + 1} \right);\)
b) \(\left( { - 4x + 3} \right)x = \left( {2x + 5} \right)x.\)
Giải các phương trình sau:
a) \({\left( {3x - 1} \right)^2} - {\left( {x + 2} \right)^2} = 0;\)
b) \(x\left( {x + 1} \right) = 2\left( {{x^2} - 1} \right).\)
Giải các phương trình:
a) \(2x\left( {x + 6} \right) + 5\left( {x + 6} \right) = 0\);
b) \(x\left( {3x + 5} \right) - 6x - 10 = 0\).
