Một đa thức hai biến bậc hai thu gọn có thể có nhiều nhất
a) bao nhiêu hạng tử bậc 2? Cho ví dụ.
b) bao nhiêu hạng tử bậc nhất? Cho ví dụ.
c) bao nhiêu hạng tử khác 0? Cho ví dụ.
Sử dụng kiến thức về hạng tử của đa thức, bậc của đa thức.
Gọi M là một đa thức bậc hai thu gọn với hai biến x và y. Khi đó:
a) Các hạng tử bậc hai của M chỉ có thể đồng dạng với một trong ba đơn thức \(xy;{x^2}\) và \({y^2}\). Do đó M có nhiều nhất là ba hạng tử bậc hai.
Ví dụ, đa thức bậc hai \({x^2}\;-2{y^2}\; + 3xy + 4\); đa thức này có 3 hạng tử bậc hai là \({x^2}; - 2{y^2}\;\) và \(3xy\).
b) Các hạng tử bậc nhất của M chỉ có thể đồng dạng với một trong hai đơn thức x và y. Do đó M có nhiều nhất là hai hạng tử bậc nhất.
Ví dụ, đa thức bậc hai \(3x - 2y + 5\); đa thức này có 2 hạng tử bậc nhất là \(3x\) và \( - 2y\).
c) Các hạng tử khác 0 của M gồm các hạng tử bậc hai, bậc nhất và một hạng tử số (hạng tử tự do). Do đó M có \(3 + 2 + 1 = 6\) hạng tử khác 0.
Ví dụ: \({x^2}\; + 2{y^2}\;-3xy + 4x-5y + 6\); đa thức này có 3 hạng tử bậc hai, 2 hạng tử bậc nhất và 1 hạng tử số.
Các bài tập cùng chuyên đề
Đa thức nêu trong tình huống mở đầu có phải đa thức thu gọn không?
Cho đa thức \(N = 5{y^2}{z^2} - 2x{y^2}z + \dfrac{1}{3}{x^4} - 2{y^2}{z^2} + \dfrac{2}{3}{x^4} + x{y^2}z\).
a) Thu gọn đa thức N.
b) Xác định hệ số và bậc của từng hạng tử (tức là bậc của từng đơn thức) trong dạng thu gọn của N.
Với mỗi đa thức sau, thu gọn (nếu cần) và tìm bậc của nó.
a) \(Q = 5{x^2} - 7xy + 2,5{y^2} + 2x - 8,3y + 1;\)
b) \(H = 4{x^5} - \dfrac{1}{2}{x^3}y + \dfrac{3}{4}{x^2}{y^2} - 4{x^5} + 2{y^2} - 7.\)
Bạn Trang nêu vấn đề: Một đa thức bậc hai thu gọn với hai biến (x và y) mà mỗi hạng tử của nó đều có hệ số bằng 1 thì có nhiều nhất là mấy hạng tử? Có ba bạn trả lời như sau:
Anh: Có 3 hạng tử
Bình: Có 5 hạng tử
Chung: Có 6 hạng tử
Em hãy nêu ý kiến của mình và cho biết đó là đa thức nào.
Thu gọn đa thức:
a) \(5{x^4} - 2{x^3}y + 20x{y^3} + 6{x^3}y - 3{x^2}{y^2} + x{y^3} - {y^4}\)
b) \(0,6{x^3} + {x^2}z - 2,7x{y^2} + 0,4{x^3} + 1,7x{y^2}\)
Thu gọn (nếu cần) và tìm bậc của mỗi đa thức sau:
a) \({x^4} - 3{x^2}{y^2} + 3x{y^2} - {x^4} + 1\)
b) \(5{x^2}y + 8xy - 2{x^2} - 5{x^2}y + {x^2}\)
Thu gọn rồi tính giá trị của đa thức:
\(M = \dfrac{1}{3}{x^2}y + x{y^2} - xy + \dfrac{1}{2}x{y^2} - 5xy - \dfrac{1}{3}{x^2}y\) tại x=0,5 và y=1.
Cho đa thức \(P = 8{x^2}{y^2}z - 2xyz + 5{y^2}z - 5{x^2}{y^2}z + {x^2}{y^2} - 3{x^2}{y^2}z.\)
a) Thu gọn và tìm bậc của đa thức P;
b) Tính giá trị của đa thức P tại x=-4;y=2 và z=1.
Trong một khách sạn có hai bể bơi dạng hình hộp chữ nhật. Bể thứ nhất có chiều sâu là 1,2 m, đáy là hình chữ nhật có chiều dài x mét, chiều rộng y mét. Bể thứ hai có chiều sâu là 1,5 m, hai kích thước đáy gấp 5 lần hai kích thước đáy của bể thứ nhất.
a) Hãy tìm đơn thức (hai biến x và y) biểu thị số mét khối nước cần có để bơm đầy cả hai bể bơi.
b) Tính lượng nước bơm đầy hai bể nếu x=5 m, y=3 m.
Tìm bậc của mỗi đa thức sau rồi tính giá trị của chúng tại x = 1; y = -2.
\(\begin{array}{l}P = 5{x^4} - 3{x^3}y + 2x{y^3} - {x^3}y + 2{y^4} - 7{x^2}{y^2} - 2x{y^3};\\Q = {x^3} + {x^2}y + x{y^2} - {x^2}y - x{y^2} - {x^3}.\end{array}\)
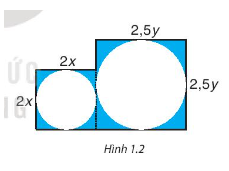
Từ một miếng bìa, người ta cắt ra hai hình tròn có bán kính x centimet và y centimet. Tìm biểu thức biểu thị diện tích phần còn lại của miếng bìa, nếu biết miếng bìa có hình dạng gồm hai hình vuông ghép lại và có kích thước (centimet) như Hình 1.2. Biểu thức đó có phải là một đa thức không? Nếu phải thì đó là đa thức bậc mấy?
Một đa thức hai biến bậc hai thu gọn có thể có nhiều nhất
a) Bao nhiêu hạng tử bậc hai? Cho ví dụ.
b) Bao nhiêu hạng tử bậc nhất? Cho ví dụ.
c) Bao nhiêu hạng tử khác 0? Cho ví dụ.
Thu gọn và tìm bậc của mỗi đa thức sau:
a) \(A = x - 2y + xy - 3x + {y^2}\)
b) \(B = xyz - {x^2}y + xz - \dfrac{1}{2}xyz + \dfrac{1}{2}xz\)
Tính giá trị của đa thức \(A = 3{x^2}y - 5xy - 2{x^2}y - 3xy\) tại \(x = 3\); \(y = - \dfrac{1}{2}\).
Thu gọn và tìm bậc của mỗi đa thức sau:
a) \(M = x - 3 - 4y + 2x - y\)
b) \(N = - {x^2}t + 13{t^3} + x{t^2} + 5{t^3} - 4\)
Tính giá trị của đa thức \(P = 3x{y^2} - 6xy + 8xz + x{y^2} - 10xz\) tại \(x = - 3\); \(y = - \dfrac{1}{2}\); \(z = 3\).
Cho đa thức: \(P = {x^3} + 2{{\rm{x}}^2}y + {x^2}y + 3{\rm{x}}{y^2} + {y^3}\)
Thực hiện phép cộng các đơn thức đồng dạng sao cho đa thức P không còn hai đơn thức nào đồng dạng.
Thu gọn đa thức: \(R = {x^3} - 2{{\rm{x}}^2}y - {x^2}y + 3{\rm{x}}{y^2} - {y^3}\)
Thu gọn mỗi đa thức sau:
a) \(A = 13{{\rm{x}}^2}y + 4 + 8{\rm{x}}y - 6{{\rm{x}}^2}y - 9\)
b) \(B = 4,4{{\rm{x}}^2}y - 40,6{\rm{x}}{y^2} + 3,6{\rm{x}}{y^2} - 1,4{{\rm{x}}^2}y - 26\)
Cho đa thức \(M = 2x{y^2} - 6xy + {y^2} + x{y^2} + 3xy + 4\)
a) Áp dụng tính chất giao hoán và kết hợp, hãy sắp xếp các đơn thức đồng dạng trong đa thức \(M\) về cùng một nhóm.
b) Viết đa thức \(M\) về dạng không còn hai hạng tử nào đồng dạng bằng cách cộng các đơn thức đồng dạng trong mỗi nhóm nêu trên.
Thu gọn đa thức sau:
\(N = 8{x^2}{y^2} - xyz - 2{x^2}{y^2} + 7xyz - 6{x^2}{y^2} + 3{x^2} + 4x - 6{x^2} + 5x + 9\)
Tìm bậc của đa thức \(N\) trong luyện tập 2.
Thu gọn rồi tính giá trị của đa thức sau tại \(x = \frac{1}{2},y = - 2\) và \(z = 1\):
\(D = {x^2} + {y^2} + {z^2} - {x^2} + {y^2} + {z^2} + {x^2} - {y^2} + {z^{2.}}\)
Cho đa thức \(P = {x^3}{y^4} - 4{x^2}{y^2} + 2{x^3}{y^4} + 5{x^2}{y^2} - 3{x^3}{y^4} + z - 1 - 4x + 6\)
a) Thu gọn đa thức \(P\).
b) Tính giá trị của đa thức \(P\) tại \(x = - 1\) và \(y = 2\)
Trong lĩnh vực khí tượng học, người ta sử dụng chỉ số nhiệt để mô tả mức độ nóng của không khí ngoài trời (chỉ số nhiệt càng lớn thì không khí càng nóng).
Để tính chỉ số nhiệt, các nhà khí tượng học sử dụng đa thức sau:
\(I = - 42 + 2x + 10y - 0,2xy - 0,007{x^2} - 0,05{y^2} + 0,001{x^2}y - 0,000002{x^2}{y^2},\)
Trong đó \(I\) là chỉ số nhiệt, \(x\) là độ ẩm \(\left( \% \right)\) và \(y\) là nhiệt độ \(\left( {^\circ F} \right)\) của không khí.
Tại một thời điểm, thành phố A có độ ẩm là 40% và nhiệt độ của không khí là \(100^\circ F\), còn thành phố B có độ ẩm là 50% và nhiệt độ của không khí là \(90^\circ F\). Tính chỉ số nhiệt của mỗi thành phố và cho biết không khí ở thành phố nào nóng hơn tại thời điểm đó.
Cho đa thức \(P = 5{x^4}{y^4} + 4{x^3}{y^2} + 2{x^3}{y^3} - 5{x^3}{y^2} - 4{x^4}{y^4} + 2y - 1 - 7y + 8\)
a) Thu gọn đa thức P
b) Tính giá trị của đa thức P tại \(x = 1\) và \(y = - 2\)
Ông Hùng dùng P (triệu đồng) để đầu tư. Ông đầu tư \(x\) (triệu đồng) vào một tài khoản ngân hàng với lãi suất 5,5% mỗi năm và đầu tư số tiền còn lại vào một quỹ tài chính với lãi suất 9% mỗi năm.
a) Viết một đa thức biểu diễn tổng số tiền ông Hùng thu được sau một năm đầu tư.
b) Tính giá trị của đa thức trong câu a tại \(P = 100,x = 25\) và cho biết ý nghĩa của nó.
Thu gọn mỗi đa thức sau:
a) \({x^2}{y^5} + 2x{y^2} - {x^2}{y^5} + \frac{{24}}{{35}}x{y^2}\)
b) \( - 11{y^2}{z^3} - 22x{y^3}{z^3} + 2{y^2}{z^3} - 33x{y^3}{z^3} - 72\)
c) \(\frac{{\sqrt 4 }}{{41}}{x^2}{y^4}{z^3} + {x^2}{y^4}z + \frac{{39}}{{41}}{x^2}{y^4}{z^3} - {x^2}{y^4}z + {z^{18}}\)
Tính giá trị của mỗi biểu thức sau:
a) \(A = - {x^3}{y^2} + 2{x^2}{y^5} - \frac{1}{2}xy\) tại \(x = 2;y = \frac{1}{2}\).
b) \(B = {y^{12}} + {x^5}{y^5} - 100{x^4}{y^4} + 100{x^3}{y^3} - 100{x^2}{y^2} + 100xy - \sqrt {36} \) tại \(x = 99;y = 0\).
c) \(C = x{y^2} + {5^2}xz - \sqrt 3 xy{z^3} + 25\) tại \(x = \frac{{ - 1}}{2};y = - \sqrt 3 ;z = 2\).
Cho đa thức \(G = \frac{1}{2}{x^2} + bx + 23\) với \(b\) là một số cho trước sao cho \(\frac{1}{2} + b\) là số nguyên. Chứng tỏ rằng: \(G\) luôn nhận giá trị nguyên tại mọi số nguyên \(x\).
