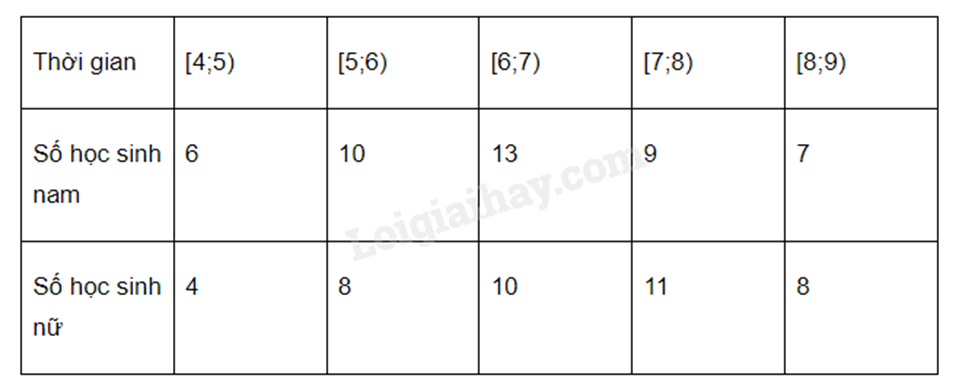
Bảng tần số ghép nhóm dưới đây thống kê số giờ ngủ buổi tối của các học sinh lớp 12A. Nếu so sánh theo khoảng tứ phân vị, nhóm học sinh nào có thời gian ngủ đồng đều hơn?
-
A.
Nhóm học sinh nam
-
B.
Nhóm học sinh nữ
-
C.
Cả hai nhóm học sinh bằng nhau
-
D.
Không so sánh được
Tính khoảng tứ phân vị của cả hai nhóm số liệu và so sánh
Tính khoảng tứ phân vị của hai nhóm học sinh và so sánh
+) Tính khoảng tứ phân vị của nhóm học sinh nam
Ta có: n = 45
Bảng tần số tích lũy
|
Thời gian |
[4;5) |
[5;6) |
[6;7) |
[7;8) |
[8;9) |
|
Số HS nam |
6 |
10 |
13 |
9 |
7 |
|
Tần số tích lũy |
6 |
16 |
29 |
38 |
45 |
Ta có: \(\frac{n}{4} = \frac{{45}}{4} = 11,25\) mà 6 < 11,25 < 16. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 11,25. Áp dụng công thức tứ phân vị thứ nhất ta có:
\({Q_1} = 5 + \frac{{11,25 - 6}}{{10}} \cdot 1 = 5,53\)
Tương tự ta tính được \({Q_3} \approx 7,53\)
Vậy khoảng tứ phân vị của nhóm học sinh nam là: \(\Delta Q = {Q_3} - {Q_1} \approx 2\)
+) Tính khoảng tứ phân vị của nhóm học sinh nữ
Ta có: n = 41
Bảng tần số tích lũy
|
Thời gian |
[4;5) |
[5;6) |
[6;7) |
[7;8) |
[8;9) |
|
Số HS nữ |
4 |
8 |
10 |
11 |
8 |
|
Tần số tích lũy |
4 |
12 |
22 |
33 |
41 |
Ta có: \(\frac{n}{4} = \frac{{41}}{4} = 10,25\) mà 4 < 10,25 < 12. Suy ra nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng 10,25. Áp dụng công thức tứ phân vị thứ nhất ta có:
\({Q_1} = 5 + \frac{{10,25 - 4}}{8} \cdot 1 \approx 5,8\)
Tương tự ta tính được \({Q_3} \approx 7,8\)
Vậy khoảng tứ phân vị của nhóm học sinh nam là: \(\Delta Q = {Q_3} - {Q_1} \approx 2\)
Do đó, khoảng tứ phân vị của hai nhóm học sinh là như nhau nên hai nhóm có số giờ ngủ đồng đều như nhau
Đáp án C.
Đáp án : C

Các bài tập cùng chuyên đề
Bài 1 :
Một người ghi lại thời gian đàm thoại của một số cuộc gọi cho kết quả như bảng sau:

Tính khoảng tứ phân vị của mẫu số liệu ghép nhóm trên.
Bài 2 :
Trong tình huống mở đầu, gọi \({y_1},{y_2},...,{y_{30}}\) là nhiệt độ cao nhất trong ngày của 30 ngày tháng Sáu năm 2022 (mẫu số liệu gốc).
a) Có thể tính chính xác khoảng tứ phân vị của mẫu số liệu gốc hay không?
b) Tìm tứ phân vị thứ nhất \({Q_1}\) và thứ phân vị thứ ba \({Q_3}\) cho mẫu số liệu ghép nhóm.
c) Hãy đưa ra một giá trị xấp xỉ cho khoảng tứ phân vị của mẫu số liệu gốc.
Bài 3 :
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:
Nhóm chứa tứ phân vị thứ nhất là:
A. \(\left[ {14;15} \right)\).
B. \(\left[ {15;16} \right)\).
C. \(\left[ {16;17} \right)\).
D. \(\left[ {17;18} \right)\).
Bài 4 :
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:
Nhóm chứa tứ phân vị thứ ba là
A. \(\left[ {15;16} \right)\).
B. \(\left[ {16;17} \right)\).
C. \(\left[ {17;18} \right)\).
D. \(\left[ {18;19} \right)\).
Bài 5 :
Một vườn thú ghi lại tuổi thọ (đơn vị: năm) của 20 con hổ và thu được kết quả như sau:
Số đặc trưng nào không sử dụng thông tin của nhóm số liệu đầu tiên và nhóm số liệu cuối cùng?
A. Khoảng biến thiên.
B. Khoảng tứ phân vị.
C. Phương sai.
D. Độ lệch chuẩn.
Bài 6 :
Thu nhập của người lao động trong một công ty được cho trong bảng sau:

Tính khoảng tứ phân vị cho số liệu này.
Bài 7 :
Xét mẫu số liệu ghép nhóm cho bởi Bảng 5.
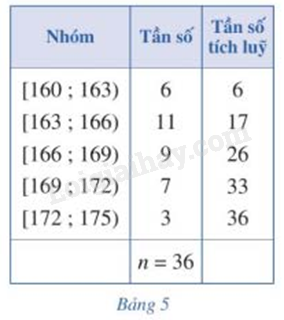
a) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{36}}{4} = 9\) có đúng không?
Tìm đầu mút trái s, độ dài h, tần số \({n_2}\) của nhóm 2; tần số tích lũy của nhóm 1. Sau đó, hãy tính tứ phân vị thứ nhất của mẫu số liệu đã cho theo công thức sau: \({Q_1} = s + \left( {\frac{{9 - c{f_1}}}{{{n_2}}}} \right).h\)
b) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{2} = \frac{{36}}{2} = 18\) có đúng không?
Tìm đầu mút trái r, độ dài d, tần số của nhóm 3; tần số tích lũy của nhóm 2. Sau đó, hãy tính tứ phân vị thứ hai của mẫu số liệu đã cho theo công thức sau: \({Q_2} = r + \left( {\frac{{18 - c{f_2}}}{{{n_3}}}} \right).d\)
c) Nhóm 4 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.36}}{4} = 27\) có đúng không?
Tìm đầu mút trái t, độ dài l, tần số của nhóm 4; tần số tích lũy của nhóm 3. Sau đó, hãy tính tứ phân vị thứ ba của mẫu số liệu đã cho theo công thức sau:\({Q_3} = t + \left( {\frac{{27 - c{f_3}}}{{{n_4}}}} \right).l\)
d) Tìm hiệu \({Q_3} - {Q_1}\)
Bài 8 :
Cho mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, thứ hai, thứ ba lần lượt là \({Q_1},{Q_2},{Q_3}\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó bằng:
A. \(2{Q_2}\)
B. \({Q_1} - {Q_3}\)
C. \({Q_3} - {Q_1}\)
D. \({Q_3} + {Q_1} - {Q_2}\)
Bài 9 :
Hãy so sánh khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình và bác An trong Khởi động.

Bài 10 :
Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:
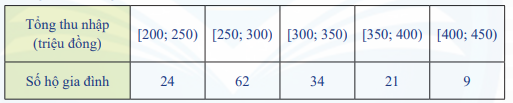
a) Hãy tìm các tứ phân vị \({Q_1}\) và \({Q_3}\).
b) Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?
Bài 11 :
Biểu đồ dưới đây biểu diễn số lượt khách hàng đặt bàn qua hình thức trực tuyến mỗi ngày trong quý III năm 2022 của một nhà hàng. Cột thứ nhất biểu diễn số ngày có từ 1 đến dưới 6 lượt đặt bàn; cột thứ hai biểu diễn số ngày có từ 6 đến dưới 11 lượt đặt bàn; …
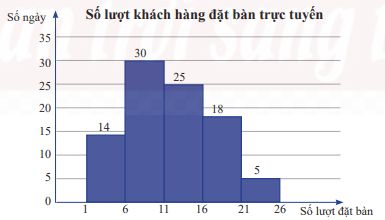
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên.
Bài 12 :
Bảng tần số ghép nhóm dưới đây thể hiện kết quả điều tra về tuổi thọ trung bình của nam giới và nữ giới ở 50 quốc gia.

a) Hãy tính các khoảng tứ phân vị của tuổi thọ trung bình của nam giới và nữ giới trong mẫu số liệu ghép nhóm trên.
b) Hãy cho biết tuổi thọ trung bình của nam giới hay nữ giới trong mẫu số liệu ghép nhóm trên đồng đều hơn.
Bài 13 :
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
-
A.
Hiệu giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu ghép nhóm đó.
-
B.
Tổng giữa tứ phân vị thứ ba và tứ phân vị thứ nhất của mẫu số liệu ghép nhóm đó.
-
C.
Hiệu giữa hai tứ phân vị bất kì của mẫu số liệu ghép nhóm đó.
-
D.
Tổng giữa hai tứ phân vị bất kì của mẫu số liệu ghép nhóm đó.
Bài 14 :
Giá trị x được gọi là giá trị ngoại lệ nếu:
-
A.
\(x < {Q_3} + 1,5\Delta Q\)
-
B.
\(x < {Q_3} - 1,5\Delta Q\)
-
C.
\(x > {Q_1} - 1,5\Delta Q\)
-
D.
\(x > {Q_3} + 1,5\Delta Q\)
Bài 15 :
Cho mẫu số liệu ghép nhóm về thời gian (phút) đi từ nhà đến nơi làm việc của các nhân viên một công ty như sau. Khoảng tứ phân vị của mẫu số liệu ghép nhóm gần nhất với số nào sau đây là:

-
A.
7.
-
B.
8.
-
C.
9.
-
D.
10.
Bài 16 :
Bảng tần số ghép nhóm dưới đây thống kê số giờ ngủ buổi tối của các học sinh lớp 12A. Khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian ngủ của các bạn nam là:
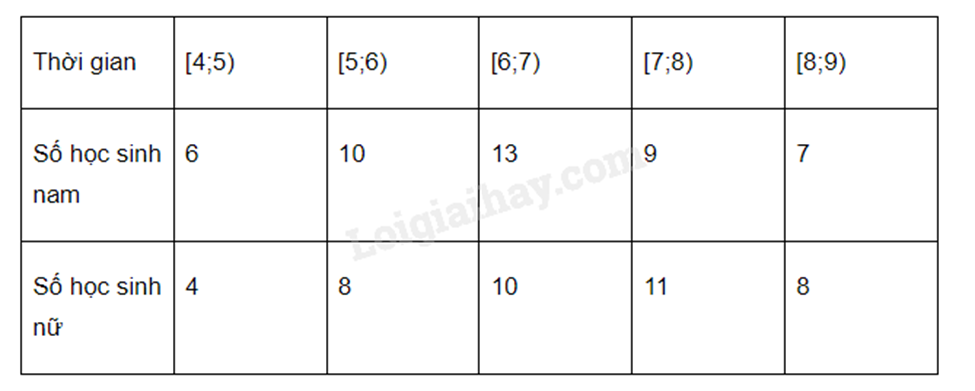
-
A.
2,09
-
B.
2
-
C.
0,29
-
D.
1,09
Bài 17 :
Khoảng tứ phân vị của mẫu số liệu ghép nhóm càng nhỏ thì?
-
A.
Dữ liệu càng tập trung xung quanh trung vị
-
B.
Dữ liệu càng phân tán
-
C.
Dữ liệu càng tập trung xung quanh số trung bình cộng
-
D.
Dữ liệu càng tập trung xung quanh mốt
Bài 18 :
Khoảng tứ phân vị dùng để đo mức độ phân tán của phần nào của mẫu số liệu?
-
A.
Nửa đầu
-
B.
Nửa giữa
-
C.
Nửa cuối
-
D.
Cả mẫu số liệu
Bài 19 :
Một bác tài xế thống kê lại độ dài quãng đường (đơn vị: km) bác đã lái xe mỗi ngày trong một tháng ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm gần bằng
-
A.
112,5
-
B.
100,13
-
C.
79,17
-
D.
82,35
Bài 20 :
Thời gian hoàn thành một bài viết chính tả của một số học sinh lớp 4 hai trường X và Y được ghi lại ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trường X bằng
-
A.
7,45
-
B.
9,65
-
C.
2,2
-
D.
8,2
Bài 21 :
Một trang trại thử nghiệm nuôi một giống cá mới. Sau 6 tháng người ta thu hoạch cho kết quả như sau:

a) Tìm khoảng tứ phân vị \({\Delta _Q}\) của mẫu số liệu ghép nhóm.
b) Khoảng tứ phân vị của mẫu số liệu gốc có phụ thuộc vào cân nặng của 10 con cá có khối lượng nhỏ nhất không? Vì sao?
Bài 22 :
Kết quả thi thử của các thí sinh tại một trung tâm tiếng Anh được cho như sau

a) Nêu các nhóm số liệu và tần số tương ứng. Giải thích thông tin của một nhóm số liệu.
b) Tìm khoảng tứ phân vị cho mẫu số liệu ghép nhóm.
Bài 23 :
Cho mẫu số liệu ghép nhóm về tuổi thọ của 20 thiết bị điện tử sau:

Khoảng tứ phân vị (làm tròn đế chữ số thập phân thứ hai) của mẫu số liệu ghép nhóm trên là
A. 2,68.
B. 4,75.
C. 6,00.
D. 7,43.
Bài 24 :
Cho mẫu số liệu ghép nhóm về tuổi thọ của 20 thiết bị điện tử sau:

Nếu thay các nhóm tương ứng bằng \(\left[ {3;5} \right),{\rm{ }}\left[ {5;7} \right),{\rm{ }}\left[ {7;9} \right),{\rm{ }}\left[ {9;11} \right)\) thì khoảng tứ phân vị sẽ thay đổi như thế nào?
A. Tăng.
B. Giảm.
C. Không thay đổi.
Bài 25 :
Biểu đồ tần số tương đối ghép nhóm sau cho biết phân bố về khối lượng của 200 bao xi măng trước khi xuất xưởng:
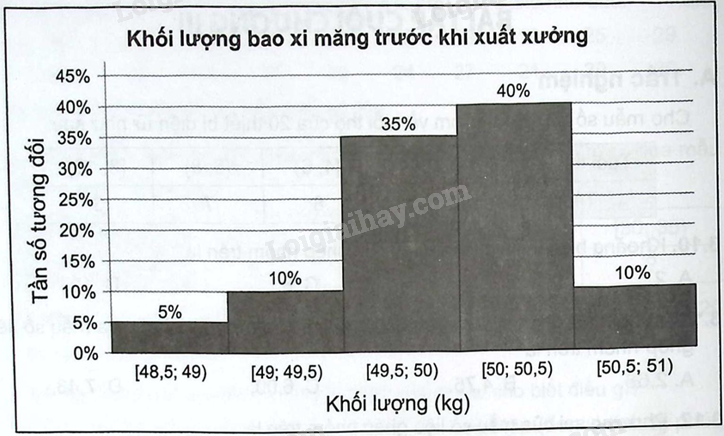
a) Lập bảng tần số ghép nhóm cho dữ liệu về khối lượng của 200 bao xi măng trên.
b) Tính khoảng tứ phân vị cho mẫu số liệu ghép nhóm thu được ở câu a.
Bài 26 :
Một mẫu số liệu ghép nhóm có tứ phân vị là \({Q_1} = 4,{Q_2} = 6,{Q_3} = 9\). Khoảng tứ phân vị của mẫu số liệu ghép nhóm đó là bao nhiêu?
A. 5.
B. 4.
C. 6.
D. 9.
Bài 27 :
Một mẫu số liệu ghép nhóm có tứ phân vị thứ nhất, thứ hai, thứ ba lần lượt là \({Q_1},{Q_2},{Q_3}\). Khoảng tứ phân vị của mẫu số liệu đó bằng:
A. \({Q_2} - {Q_1}\).
B. \({Q_3} - {Q_1}\).
C. \({Q_3} - {Q_2}\).
D. \({Q_3} + {Q_1} - {Q_2}\).
Bài 28 :
Hình 3.3 là biểu đồ biểu diễn nhiệt độ trung bình hằng tháng của hai địa phương Y, Z.
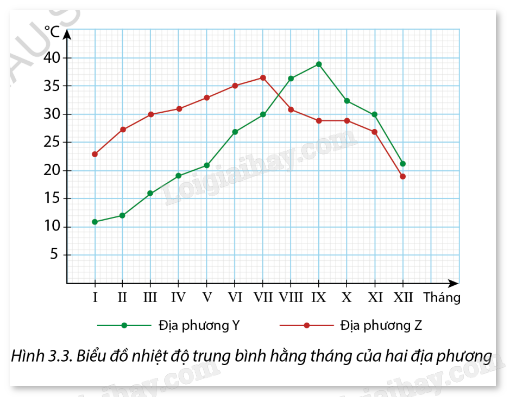
a) Lập bảng số liệu ghép nhóm về nhiệm độ của hai địa phương Y, Z, với độ dài các nhóm là 5 và đầu mút phải của nhóm cuối cùng là 40.
b) Tìm khoảng tứ phân vị của nhiệt độ mỗi địa phương và cho biết nhiệt độ của địa phương nào ít biến động hơn.
Bài 29 :
Ở một phòng điều trị nội trú của bệnh viện, dữ liệu thống kê thời gian ngủ hằng đêm của hai bệnh nhân trong suốt một tháng được tổng hợp bởi hai bảng dưới đây:
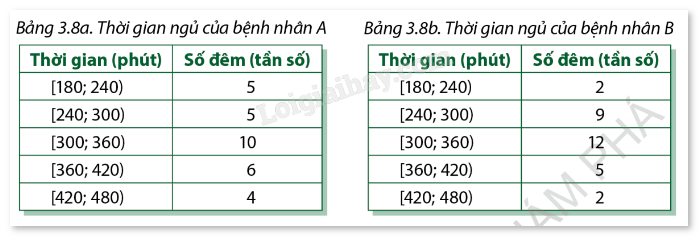
Bệnh nhân nào có thời gian ngủ ổn định hơn?
Bài 30 :
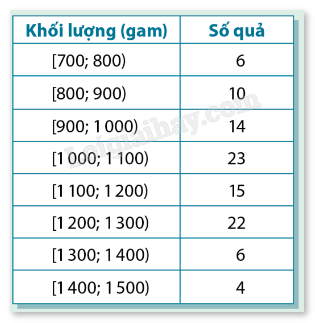
Trở lại với bảng 3.1 về khối lượng của 100 quả dứa giống E. Để tiện tính toán, ta biểu diễn dữ liệu bằng một bảng hai cột như bảng trên.
a) Hãy tính các tứ phân vị của mẫu số liệu cho trong bảng.
b) Đề xuất một cách ước tính khoảng tứ phân vị của mẫu số liệu ghép nhóm đã cho.


















Danh sách bình luận