Cho hình vuông ABCD có cạnh bằng 1 và một điểm O tùy ý. Tính độ dài của các vectơ sau:
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} ;\)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\).
Bước 1: Thay thế vectơ bằng nhau rồi tìm tổng.
Bước 2: Tìm độ dài vectơ vừa tìm đc, độ dài vectơ \(\overrightarrow {AB} \) là \(\left| {\overrightarrow {AB} } \right| = AB\).
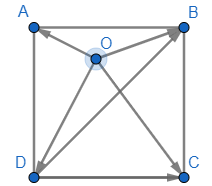
Ta có: \(AB = BC = CD = DA = 1;\)
\(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{1^2} + {1^2}} = \sqrt 2 \)
a) \(\overrightarrow a = \overrightarrow {OB} - \overrightarrow {OD} = \overrightarrow {OB} + \overrightarrow {DO} = \left( {\overrightarrow {DO} + \overrightarrow {OB} } \right) = \overrightarrow {DB} \)
\( \Rightarrow \left| {\overrightarrow a } \right| = \left| {\overrightarrow {DB} } \right| = DB = \sqrt 2 \)
b) \(\overrightarrow b = \left( {\overrightarrow {OC} - \overrightarrow {OA} } \right) + \left( {\overrightarrow {DB} - \overrightarrow {DC} } \right)\)
\( = \left( {\overrightarrow {OC} + \overrightarrow {AO} } \right) + \left( {\overrightarrow {DB} + \overrightarrow {CD} } \right) = \left( {\overrightarrow {AO} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {CD} + \overrightarrow {DB} } \right)\)
\( = \overrightarrow {AC} + \overrightarrow {CB} = \overrightarrow {AB} \)
\( \Rightarrow \left| {\overrightarrow b } \right| = \left| {\overrightarrow {AB} } \right| = AB = 1\)
Chú ý khi giải:
Khi có dấu trừ phía trước ta thường thay bằng vectơ đối của nó và ngược lại

Các bài tập cùng chuyên đề
Bài 1 :
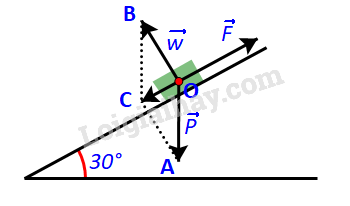
Tính lực kéo cần thiết để kéo một khẩu pháo có trọng lượng 22 148 N (ứng với khối lượng xấp xỉ 2 260kg) lên một con dốc nghiêng \({30^o}\) so với phương nằm ngang (H.4.18). Nếu lực kéo của mỗi người bằng 100N, thì cần tối thiểu bao nhiêu người để kéo pháo?
Bài 2 :
Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng: \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 .\)
Bài 3 :
Cho tam giác ABC có M là trung điểm AC, N là trung điểm BC và AB = a. Tính độ dài vecto \(\overrightarrow {CM} - \overrightarrow {NB} \).
Bài 4 :
Cho hai vecto \(\overrightarrow a \),\(\overrightarrow b \). Lấy một điểm M tùy ý.
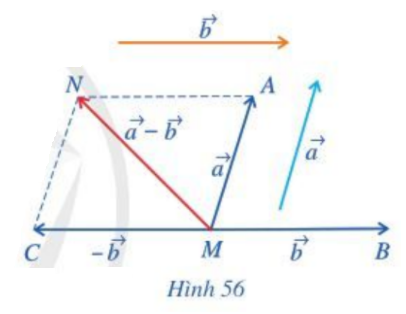
a) Vẽ \(\overrightarrow {MA} = \overrightarrow a ,\;\overrightarrow {MB} = \overrightarrow b ,\;\overrightarrow {MC} = - \overrightarrow b \) (Hình 56)
b) Tổng của hai vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) bằng vecto nào?
Bài 5 :
Cho ba điểm D, E, G. Vecto \(\overrightarrow v = \overrightarrow {DE} + ( - \overrightarrow {DG} )\) bằng vecto nào sau đây?
A. \(\overrightarrow {EG} \)
B. \(\overrightarrow {GE} \)
C. \(\overrightarrow {GD} \)
D. \(\overrightarrow {ED} \)
Bài 6 :
Cho ABCD là hình bình hành. Chứng minh \(\overrightarrow {MB} - \overrightarrow {MA} = \overrightarrow {MC} - \overrightarrow {MD} \) với mỗi điểm M trong mặt phẳng.
Bài 7 :
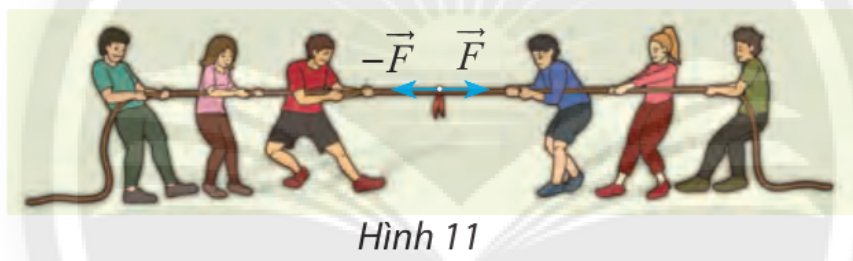
Tìm hợp lực của hai lực đối nhau \(\overrightarrow F \) và \( - \overrightarrow F \) (hình 11)


















Danh sách bình luận