Luyện tập – vận dụng 2 trang 58 SGK Toán 10 tập 1 – Cánh diều
Giải phương trình: \(\sqrt {3x - 5} = x - 1\)
Bước 1. Giải bất phương trình \(x - 1 \ge 0\) để tìm tập nghiệm của bất phương trình đó.
Bước 2. Bình phương hai vế của phương trình rồi tìm tập nghiệm.
Bước 3. Trong những nghiệm của phương trình ở bước 2, ta chỉ giữ lại những nghiệm thuộc tập nghiệm của bất phương trình \(x - 1 \ge 0\). Tập nghiệm giữ lại đó chính là tập nghiệm của phương trình đã cho.
\(x - 1 \ge 0 \Leftrightarrow x \ge 1\)
Bình phương hai vế của phương trình ta được
\(3x - 5 = {\left( {x - 1} \right)^2}\)\( \Leftrightarrow {x^2} - 5x + 6 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = 2\left( {TM} \right)\\x = 3\left( {TM} \right)\end{array} \right.\)
Vậy tập nghiệm của phương trình đã cho là \(S = \left\{ {2;3} \right\}\)
Các bài tập cùng chuyên đề
Giải các phương trình sau:
a) \(\sqrt {2 - x} + 2x = 3\)
b) \(\sqrt { - {x^2} + 7x - 6} + x = 4\)
Trong các phát biểu sau, phát biểu nào là đúng?
A. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\) là tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\)
B. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\) là tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) thỏa mãn bất phương trình \(g\left( x \right) \ge 0\)
C. Tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) là tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\)
D. Tập nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\) là tập nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) thỏa mãn bất phương trình \(f\left( x \right) \ge 0\)
Giải thích vì sao chỉ cần kiểm tra nghiệm của phương trình \(f\left( x \right) = {\left[ {g\left( x \right)} \right]^2}\) thỏa mãn bất phương trình \(g\left( x \right) \ge 0\) mà không cần kiểm tra thỏa mãn bất phương trình \(f\left( x \right) \ge 0\) để kết luận nghiệm của phương trình \(\sqrt {f\left( x \right)} = g\left( x \right)\).
Giải các phương trình sau:
a) \(\sqrt {7 - 2x} + x = 2\)
b) \(\sqrt { - 2{x^2} + 7x + 1} + 3x = 7\)
Giải các phương trình sau:
a) \(\sqrt {8 - x} + x = - 4\)
b) \(\sqrt {3{x^2} - 5x + 2} + 3x = 4\)
Bác Việt sống và làm việc tại trạm hải đăng cách bờ biển 4km. Hằng tuần bác chèo thuyền vào vị trí gần nhất trên bờ biển là bến Bính để nhận hàng hóa do cơ quan cung cấp. Tuần này, do trục trặc về vận chuyển nên toàn bộ số hàng vẫn đang nằm ở Thôn Hoành, bên bờ biển cách bến Bính 9,25 km và sẽ được anh Nam vận chuyển trên con đường dọc bờ biển tới bến Bính bằng xe kéo. Bác Việt đã gọi điện thống nhất với anh Nam là họ sẽ gặp nhau ở vị trí nào đó giữa bến Bính và thôn Hoành để hai người có mặt tại đó cùng lúc, không mất thời gian cờ nhau. Tìm vị trí hai người dự định gặp nhau, biết rằng vận tốc kéo xe của anh Nam là 5 km/h và thuyền của bác Việt di chuyển với vân tốc 4 km/h. Ngoài ra giả thiết rằng đường bờ biển từ thôn Hoành đến bến Bính là đường thẳng và bác Việt cũng chèo thuyền tới một điểm trên bờ biền theo một đường thẳng.
Giải các phương trình sau:
a) \(\sqrt {2{x^2} + x + 3} = 1 - x\)
b) \(\sqrt {3{x^2} - 13x + 14} = x - 3\)
Cho phương trình \(\sqrt {26{x^2} - 63x + 38} = 5x - 6\)
a) Bình phương hai vế và giải phương trình nhận được.
b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không.
Giải các phương trình sau:
a) \(\sqrt {6{x^2} + 13x + 13} = 2x + 4\)
b) \(\sqrt {2{x^2} + 5x + 3} = - 3 - x\)
c) \(\sqrt {3{x^2} - 17x + 23} = x - 3\)
d) \(\sqrt { - {x^2} + 2x + 4} = x - 2\)
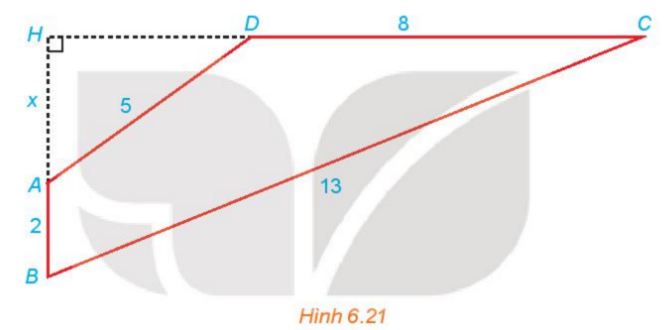
Cho từ giác ABCD có \(AB \bot CD;AB = 2;BC = 13;CD = 8;DA = 5\) (H.6.21). Gọi H là giao điểm của AB và CD và đặt x=AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD.
Tập nghiệm của phương trình \(\sqrt {2{x^2} - 3} = x - 1\) là:
A. \(\left\{ { - 1 - \sqrt 5 ; - 1 + \sqrt 5 } \right\}.\)
B. \(\left\{ { - 1 - \sqrt 5 } \right\}.\)
C. \(\left\{ { - 1 + \sqrt 5 } \right\}.\)
D. \(\emptyset .\)
Giải phương trình \(\sqrt {3{x^2} + 27x - 41} = 2x + 3\).
Lời giải cho phương trình \(\sqrt { - {x^2} + x + 1} = x\) như sau đúng hai sai?
\(\)\(\sqrt { - {x^2} + x + 1} = x\)
\( \Rightarrow - {x^2} + x + 1 = {x^2}\) (bình phương cả hai vế để làm mất dấu căn)
\( \Rightarrow - 2{x^2} + x + 1 = 0\) (chuyển vế, rút gọn)
\( \Rightarrow x = 1\) hoặc \(x = - \frac{1}{2}\) (giải phương trình bậc hai)
Vậy phương trình đã cho có hai nghiệm là 1 và \( - \frac{1}{2}\)
Giải các phương trình sau:
a) \(\sqrt {{x^2} + 3x + 1} = 3\)
b) \(\sqrt {{x^2} - x - 4} = x + 2\)
c) \(2 + \sqrt {12 - 2x} = x\)
d) \(\sqrt {2{x^2} - 3x - 10} = - 5\)
Giải các phương trình sau:
a) \(\sqrt {2{x^2} - 13x + 16} = 6 - x\)
b) \(\sqrt {3{x^2} - 33x + 55} = x - 5\)
c) \(\sqrt { - {x^2} + 3x + 1} = x - 4\)
Giải các phương trình sau:
a) \(\sqrt {2x - 3} = x - 3\)
b) \((x - 3)\sqrt {{x^2} + 4} = {x^2} - 9\)
Số nghiệm của phương trình \(\sqrt {{x^2} + 4x - 2} = x - 3\) (1) là:
A. 0
B. 1
C. 2
D. 3
Tập nghiệm của phương trình \(\sqrt {2{x^2} - 9x - 9} = 3 - x\) (1) là:
A. \(S = {\rm{\{ }}6\} \)
B. \(S = \emptyset \)
C. \(S = {\rm{\{ }} - 3\} \)
D. \(S = {\rm{\{ }} - 3;6\} \)
Cho hình chữ nhật ABCD có AB = 6 cm, AD = 13 cm. Tìm vị trí điểm M trên cạnh AD sao cho BM = 2MD.
Giải các phương trình sau:
a) \(\sqrt {4{x^2} + 15x - 19} = \sqrt {5{x^2} + 23x - 14} \)
b) \(\sqrt {8{x^2} + 10x - 3} = \sqrt {29{x^2} - 7x - 1} \)
c) \(\sqrt { - 4{x^2} - 5x + 8} = \sqrt {2{x^2} + 2x - 2} \)
d) \(\sqrt {5{x^2} + 25x + 13} = \sqrt {20{x^2} - 9x + 28} \)
e) \(\sqrt { - {x^2} - 2x + 7} = \sqrt { - x - 13} \)
Giải các phương trình sau:
a) \(\sqrt { - {x^2} + 7x + 13} = 5\)
b) \(\sqrt { - {x^2} + 3x + 7} = 3\)
c) \(\sqrt {69{x^2} - 52x + 4} = - 6x + 4\)
d) \(\sqrt { - {x^2} - 4x + 22} = - 2x + 5\)
e) \(\sqrt {4x + 30} = 2x + 3\)
g) \(\sqrt { - 57x + 139} = 3x - 11\)
Giải các phương trình sau:
a) \(\sqrt { - 7{x^2} - 60x + 27} + 3\left( {x - 1} \right) = 0\)
b) \(\sqrt {3{x^2} - 9x - 5} + 2x = 5\)
c) \(\sqrt { - 2x + 8} - x + 6 = x\)
Khẳng định nào sau đây đúng với phương trình \(\sqrt {5{x^2} + 27x + 36} = 2x + 5\)?
A. Phương trình có một nghiệm
B. Phương trình vô nghiệm
C. Tổng các nghiệm của phương trình là \( - 7\)
D. Các nghiệm của phương trình đều không bé hơn \( - \frac{5}{2}\)
Tập nghiệm S của phương trình \(\sqrt {2x - 3} = x - 3\) là
Số nghiệm của phương tình \(\sqrt {3{x^2} - 9x + 7} = x - 2\) là
Nghiệm của phương trình \(\sqrt {{x^2} + 3x - 2} = \sqrt {x + 1} \) là
