Chất điểm A chịu tác động của ba lực \(\overrightarrow {{F_1}} ,\;\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) như hình 4.30 và ở trạng thái cân bằng (tức là \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)). Tính độ lớn của các lực \(\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \) biết \(\overrightarrow {{F_1}} \) có độ lớn là 20N.
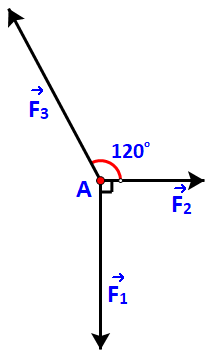
Bước 1: Xác định vecto \(\overrightarrow u = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \). Từ trạng thái của chất điểm suy ra mối liên hệ (phương, chiều, độ lớn) giữa \(\overrightarrow u \) và \(\overrightarrow {{F_3}} \).
Bước 2: Tính độ lớn của \(\overrightarrow {{F_2}} ,\;\overrightarrow {{F_3}} \).
Bước 1: Đặt \(\overrightarrow u = \overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} \). Ta xác định các điểm như hình dưới.
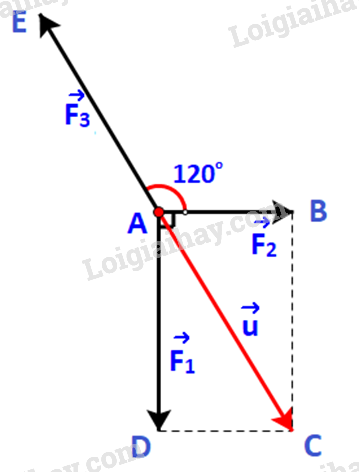
Dễ dàng xác định điểm C, là điểm thứ tư của hình bình hành ABCD. Do đó vecto \(\overrightarrow u \) chính là vecto \(\overrightarrow {AC} \)
Vì chất điểm A ở trang thái cân bằng nên \(\overrightarrow {{F_1}} + \;\overrightarrow {{F_2}} + \;\overrightarrow {{F_3}} = \overrightarrow 0 \) hay \(\;\overrightarrow u + \;\overrightarrow {{F_3}} = \overrightarrow 0 \)
\( \Leftrightarrow \;\overrightarrow u \) và \(\;\overrightarrow {{F_3}} \) là hai vecto đối nhau.
\( \Leftrightarrow A\) là trung điểm của EC.
Bước 2:
Ta có: \(\left| {\overrightarrow {{F_1}} } \right| = AD = 20,\;\left| {\overrightarrow {{F_2}} } \right| = AB,\;\left| {\overrightarrow {{F_3}} } \right| = AC.\)
Do A, C, E thẳng hàng nên \(\widehat {CAB} = {180^o} - \widehat {EAB} = {60^o}\)
\(\begin{array}{l} \Rightarrow \widehat {CAD} = {90^o} - {60^o} = {30^o}\\ \Rightarrow \left\{ \begin{array}{l}AC = \frac{{AD}}{{\cos {{30}^o}}} = \frac{{40\sqrt 3 }}{3};\;\\AB = DC = AC.\sin {30^o} = \frac{{20\sqrt 3 }}{3}.\end{array} \right.\end{array}\)
Vậy \(\;\left| {\overrightarrow {{F_2}} } \right| = \frac{{20\sqrt 3 }}{3},\;\;\left| {\overrightarrow {{F_3}} } \right| = \frac{{40\sqrt 3 }}{3}.\)
Các bài tập cùng chuyên đề
Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu thị \(\overrightarrow {AM} \) theo hai vecto \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \).
Cho tứ giác ABCD. Gọi M, N tương ứng là trung điểm của các cạnh AB, CD. Chứng minh \(\overrightarrow {BC} + \overrightarrow {AD} = 2\overrightarrow {MN} = \;\overrightarrow {AC} + \overrightarrow {BD} .\)
Cho hai điểm phân biệt A và B.
a) Hãy xác định điểm K sao cho \(\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OK} = \frac{1}{3}\overrightarrow {OA} + \frac{2}{3}\overrightarrow {OB} .\)
Cho tam giác ABC
a) Hãy xác định điểm M để \(\overrightarrow {MA} + \overrightarrow {MB} + 2\overrightarrow {MC} = \overrightarrow 0 \)
b) Chứng minh rằng với mọi điểm O, ta có \(\overrightarrow {OA} + \overrightarrow {OB} + 2\overrightarrow {OC} = 4\overrightarrow {OM} \)
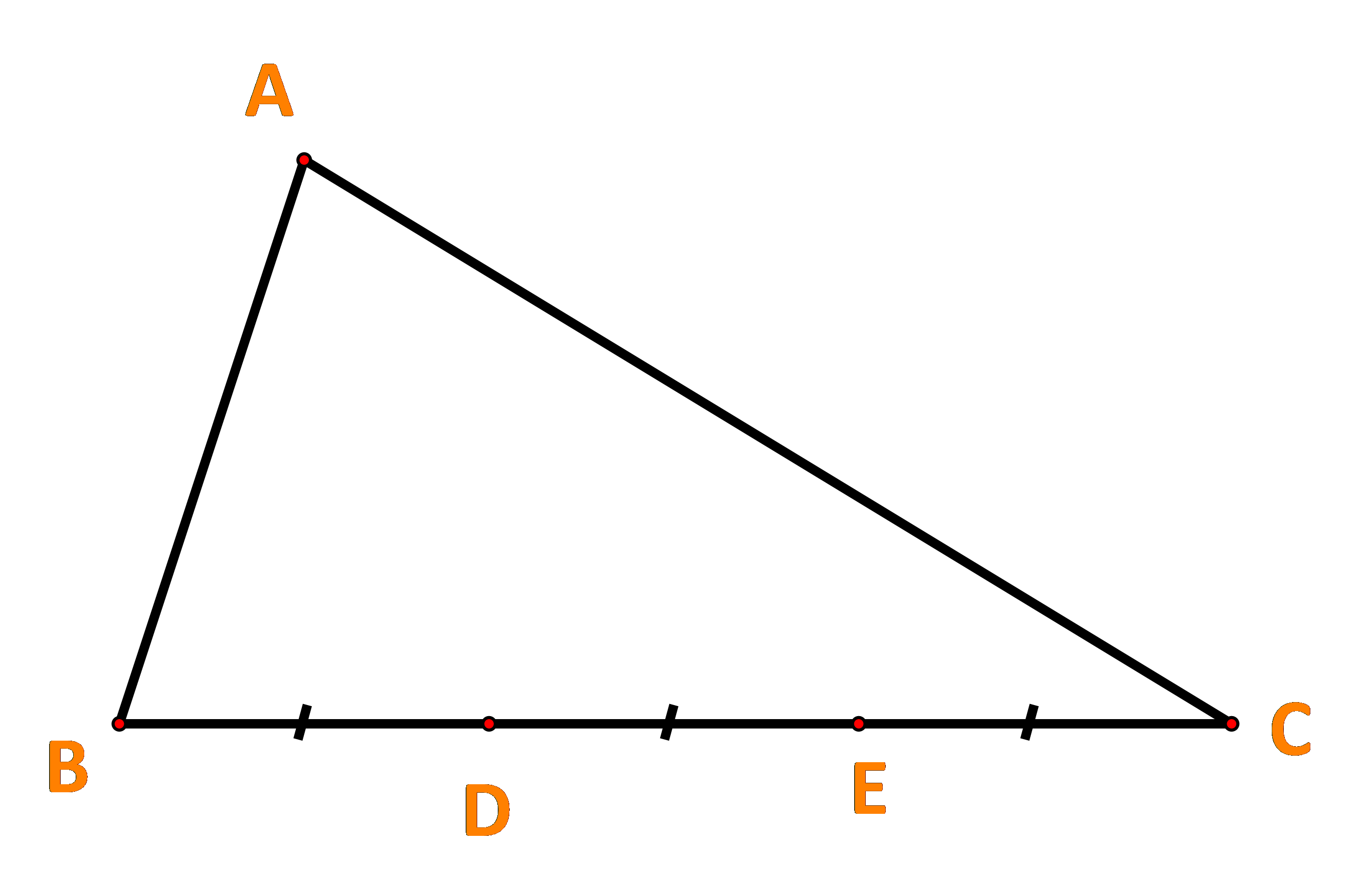
Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62). Giả sử \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AC} = \overrightarrow b .\) Biểu diễn các vecto \(\overrightarrow {BC} ,\overrightarrow {BD} ,\overrightarrow {BE} ,\overrightarrow {AD} ,\overrightarrow {AE} \) theo \(\overrightarrow a ,\overrightarrow b .\)
Cho tam giác ABC. Các điểm D, E, H thỏa mãn
\(\overrightarrow {DB} = \frac{1}{3}\overrightarrow {BC} ,\;\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AC} ,\;\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} .\)
a) Biểu thị mỗi vecto \(\overrightarrow {AD} ,\overrightarrow {DH} ,\overrightarrow {HE} \) theo hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} .\)
b) Chứng minh D, E, H thẳng hàng.
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:
a) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
b) \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AC} \)
Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng
a) \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cho hai điểm phân biệt A và B. Xác định điểm M sao cho \(\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0 \)
Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MG} \)
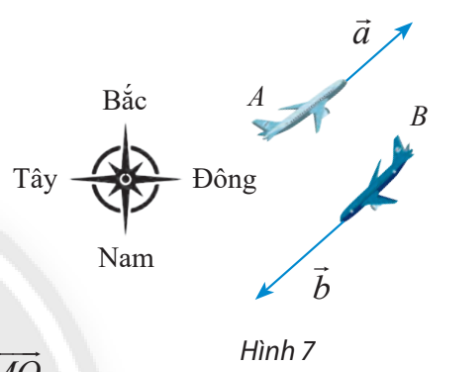
Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc \(\overrightarrow b \)của máy bay B theo vectơ vận tốc \(\overrightarrow a \) của máy bay A
Cho 2 điểm phân biệt A và B
a) Xác định điểm O sao cho \(\overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0 \)
b) Chứng minh rằng với mọi điểm M, ta có \(\overrightarrow {MA} + 3\overrightarrow {MB} = 4\overrightarrow {MO} \)
Cho tam giác \(ABC.\) Gọi \(D,\,\,E\) tương ứng là trung điểm của \(BC,\,\,CA.\) Hãy biểu thị các vectơ \(\overrightarrow {AB} ,\,\,\overrightarrow {BC} ,\,\,\overrightarrow {CA} \) theo các vectơ \(\overrightarrow {AD} \) và \(\overrightarrow {BE} .\)
Cho hình bình hành \(ABCD.\) Gọi \(M,\,\,N\) theo thứ tự là trung điểm các cạnh \(AB,\,\,CD.\) Lấy \(P\) thuộc đoạn \(DM\) và \(Q\) thuộc đoạn \(BN\) sao cho \(DP = 2PM,\,\,BQ = xQN.\) Đặt \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AD} = \overrightarrow v .\)
a) Hãy biểu thị các vectơ \(\overrightarrow {AP} ,\,\,\overrightarrow {AQ} \) qua hai vectơ \(\overrightarrow u \) và \(\overrightarrow v .\)
b) Tìm \(x\) để \(A,\,\,P,\,\,Q\) thẳng hàng.
Cho tam giác \(ABC\) với trọng tâm \(G.\) Lấy điểm \(A',\,\,B'\) sao cho \(\overrightarrow {AA'} = 2\overrightarrow {BC} ,\,\,\overrightarrow {BB'} = 2\overrightarrow {CA} .\) Gọi \(G'\) là trọng tâm của tam giác \(A'B'C.\) Chứng minh rằng \(GG'\) song song với \(AB.\)
Cho tứ giác lồi \(ABCD,\) không có hai cạnh nào song song. Gọi \(E,\,\,F\) theo thứ tự là trung điểm của \(AB,\,\,CD.\) Gọi \(K,\,\,L,\,\,M,\,\,N\) lần lượt là trung điểm của \(AF,\,\,CE,\,\,BF,\,\,DE.\)
a) Chứng minh rằng tứ giác \(KLMN\) là một hình bình hành.
b) Gọi \(I\) là giao điểm của \(KM,\,\,LN.\) Chứng minh rằng \(E,\,\,I,\,\,F\) thẳng hàng.
Cho ba điểm phân biệt I, A, B và số thực k ≠ 1 thoả mãn \(\overrightarrow {IA} = k\overrightarrow {IB} \). Chứng minh rằng với O là điểm bất kì ta có:
\(\overrightarrow {OI} = \left( {\frac{1}{{1 - k}}} \right)\overrightarrow {OA} - \left( {\frac{k}{{1 - k}}} \right)\overrightarrow {OB} \) (*)
Cho hình bình hành ABCD có G là trọng tâm của tam giác ABD.
Chứng minh rằng: \(\overrightarrow {AC} = 3\overrightarrow {AG} \).
Cho hai điểm phân biệt A và B. Tìm điểm K sao cho \(3\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
Cho tam giác đều ABC cạnh 4. Vectơ \( - \frac{1}{2}\overrightarrow {BC} \) có độ dài là.
Biết \(\overrightarrow {AB} = \overrightarrow a \). Gọi C là điểm thỏa mãn \(\overrightarrow {CA} = \overrightarrow {AB} \). Chọn khẳng định đúng.
