a) \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
Bước 1: Vẽ đường tròn lượng giác, lấy điểm M biểu diễn góc \(\alpha \) bất kì.
Bước 2: Xác định \(\sin \alpha ,\;\cos \alpha \)( tương ứng với tung độ và hoành độ của điểm M).
Bước 3: Suy ra đẳng thức cần chứng minh.
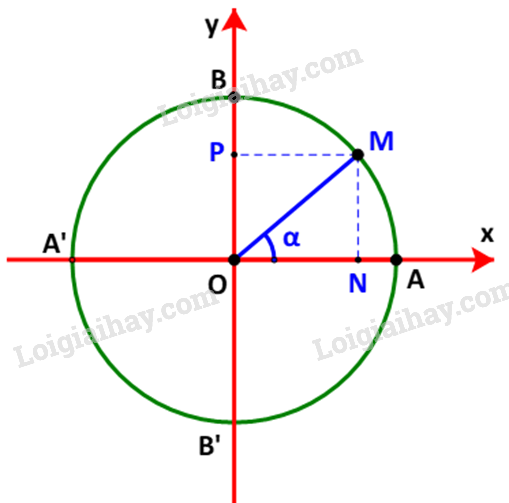
Gọi M(x;y) là điểm trên đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.
Ta có: \(\left\{ \begin{array}{l}x = \cos \alpha \\y = \sin \alpha \end{array} \right. \Rightarrow \left\{ \begin{array}{l}{\cos ^2}\alpha = {x^2}\\{\sin ^2}\alpha = {y^2}\end{array} \right.\)(1)
Mà \(\left\{ \begin{array}{l}\left| x \right| = ON\\\left| y \right| = OP = MN\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x^2} = {\left| x \right|^2} = O{N^2}\\{y^2} = {\left| y \right|^2} = M{N^2}\end{array} \right.\)(2)
Từ (1) và (2) suy ra \({\sin ^2}\alpha + {\cos ^2}\alpha = O{N^2} + M{N^2} = O{M^2}\) (do \(\Delta OMN\) vuông tại N)
\( \Rightarrow {\sin ^2}\alpha + {\cos ^2}\alpha = 1\) (vì OM =1). (đpcm)

Các bài tập cùng chuyên đề
Bài 1 :
Trong các khẳng định sau, khẳng định nào đúng?
-
A.
$\sin {743^0} = \sin {23^0}$
-
B.
$\sin {743^0} = - \sin {23^0}$
-
C.
$\sin {743^0} = \cos {\rm{2}}{{\rm{3}}^0}$
-
D.
$\sin {743^0} = - \cos {\rm{2}}{{\rm{3}}^0}$
Bài 2 :
Giá trị của biểu thức $S = 3 - {\rm{si}}{{\rm{n}}^2}{\rm{9}}{0^0} + {\rm{ 2co}}{{\rm{s}}^2}{\rm{6}}{{\rm{0}}^0}{\rm{ - 3ta}}{{\rm{n}}^2}{45^0}$ bằng:
-
A.
\(\dfrac{1}{2}\)
-
B.
$\dfrac{{ - 1}}{2}$
-
C.
\(1\)
-
D.
\(3\)
Bài 3 :
Giá trị $\cot \dfrac{{89\pi }}{6}$ là
-
A.
$\sqrt 3 $.
-
B.
$ - \sqrt 3 $.
-
C.
$\dfrac{{\sqrt 3 }}{3}$.
-
D.
$-\dfrac{{\sqrt 3 }}{3}$.
Bài 4 :
Cho biết \(\frac{\pi }{2} < x < \pi \) và \(\sin \left( x \right) = \frac{1}{3}\). Tính \(\cos \left( x \right)\).
-
A.
\(\cos \left( x \right) = \frac{2}{3}\)
-
B.
\(\cos \left( x \right) = - \frac{2}{3}\)
-
C.
\(\cos \left( x \right) = \frac{{2\sqrt 2 }}{3}\)
-
D.
\(\cos \left( x \right) = - \frac{{2\sqrt 2 }}{3}\)
Bài 5 :
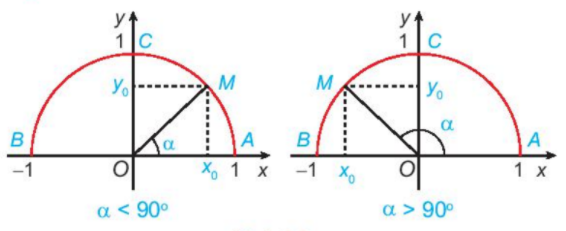
a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:
\(\begin{array}{l}\alpha = {90^o};\\\alpha < {90^o};\\\alpha > {90^o}.\end{array}\)
b) Khi \({0^o} < \alpha < {90^o}\), nêu mối quan hệ giữa \(\cos \alpha ,\;\sin \alpha \) với hoành độ và tung độ của điểm M.
Bài 6 :
c) \(1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\quad ({0^o} < \alpha < {180^o})\)
Bài 7 :
b) \(1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\quad (\alpha \ne {90^o})\)
Bài 8 :
Cho góc \(\alpha \;\;({0^o} < \alpha < {180^o})\) thỏa mãn \(\tan \alpha = 3\)
Tính giá trị biểu thức: \(P = \frac{{2\sin \alpha - 3\cos \alpha }}{{3\sin \alpha + 2\cos \alpha }}\)
Bài 9 :
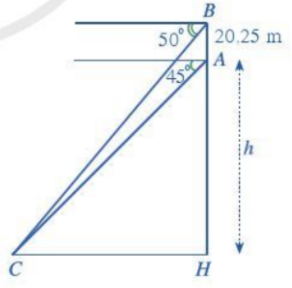
Hãy tính chiều cao h của đỉnh Lũng Cú so với chân núi trong bài toán ở phần mở đầu.
Bài 10 :
Tìm các giá trị lượng giác của góc \({135^o}\)
Bài 11 :
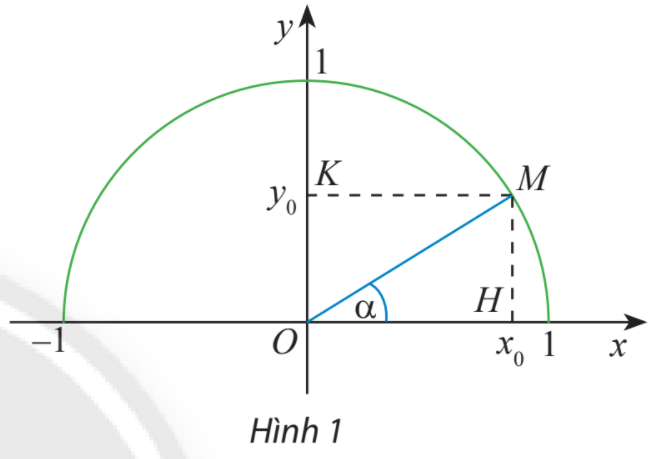
Trong mặt phẳng tọa độ Oxy, nửa đường tròn tâm O bán kính \(R = 1\) nằm phía trên trục hoành được gọi là nửa đường tròn đơn vị. Cho trước một góc nhọn \(\alpha ,\)lấy điểm M trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = \alpha .\) Giả sử điểm M có tọa độ \(({x_0};{y_0}).\) Trong tam giác vuông OHM, áp dụng cách tính các tỉ số lượng giác của một góc nhọn đã học ở lớp 9, chứng tỏ rằng:
\(\sin \alpha = {y_0};\;\cos \alpha = {x_0};\;\tan \alpha = \frac{{{y_0}}}{{{x_0}}};\;\cot \alpha = \frac{{{x_0}}}{{{y_0}}}.\)
Bài 12 :
Cho góc \(\alpha \) tù. Khẳng định nào sau đây đúng?
-
A.
\(\tan \alpha > 0\)
-
B.
\(\sin \alpha < 0\)
-
C.
\(\cos \alpha > 0\)
-
D.
\(\cot \alpha < 0\)
Bài 13 :
Cho góc \(\alpha \) nhọn. Khẳng định nào sau đây đúng?
-
A.
\(\tan \alpha > 0\)
-
B.
\(\sin \alpha < 0\)
-
C.
\(\cos \alpha < 0\)
-
D.
\(\cot \alpha < 0\)
Bài 14 :
Tam giác \(ABC\) có \(\widehat A = {15^ \circ },\,\,\widehat B = {45^ \circ }.\) Giá trị của \(\tan C\) bằng:
A. \( - \sqrt 3 .\)
B. \(\sqrt 3 .\)
C. \(\frac{1}{{\sqrt 3 }}.\)
D. \( - \frac{1}{{\sqrt 3 }}.\)
Bài 15 :
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {135^ \circ }.\) Tích hoành độ và tung độ của điểm \(M\) bằng
A. \(\frac{1}{{2\sqrt 2 }}.\)
B. \(\frac{1}{2}\)
C. \( - \frac{1}{2}\)
D. \( - \frac{1}{{2\sqrt 2 }}.\)
Bài 16 :
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }.\) \(N\) là điểm đối xứng với \(M\) qua trục tung. Giá trị của \(\tan \widehat {xON}\) bằng:
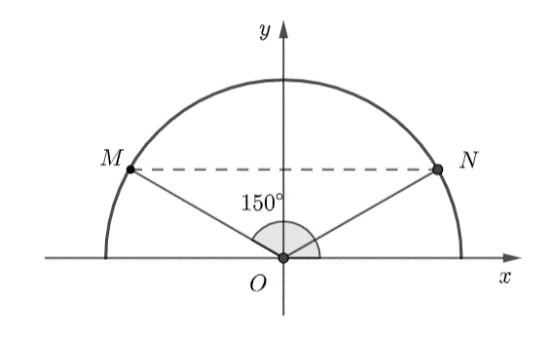
A. \(\frac{1}{{\sqrt 3 }}.\)
B. \( - \frac{1}{{\sqrt 3 }}.\)
C. \(\sqrt 3 .\)
D. \( - \sqrt 3 .\)
Bài 17 :
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị, sao cho \(\cos \widehat {xOM} = \frac{{ - 3}}{5}.\) (H.3.4). Diện tích của tam giác \(AOM\) bằng:
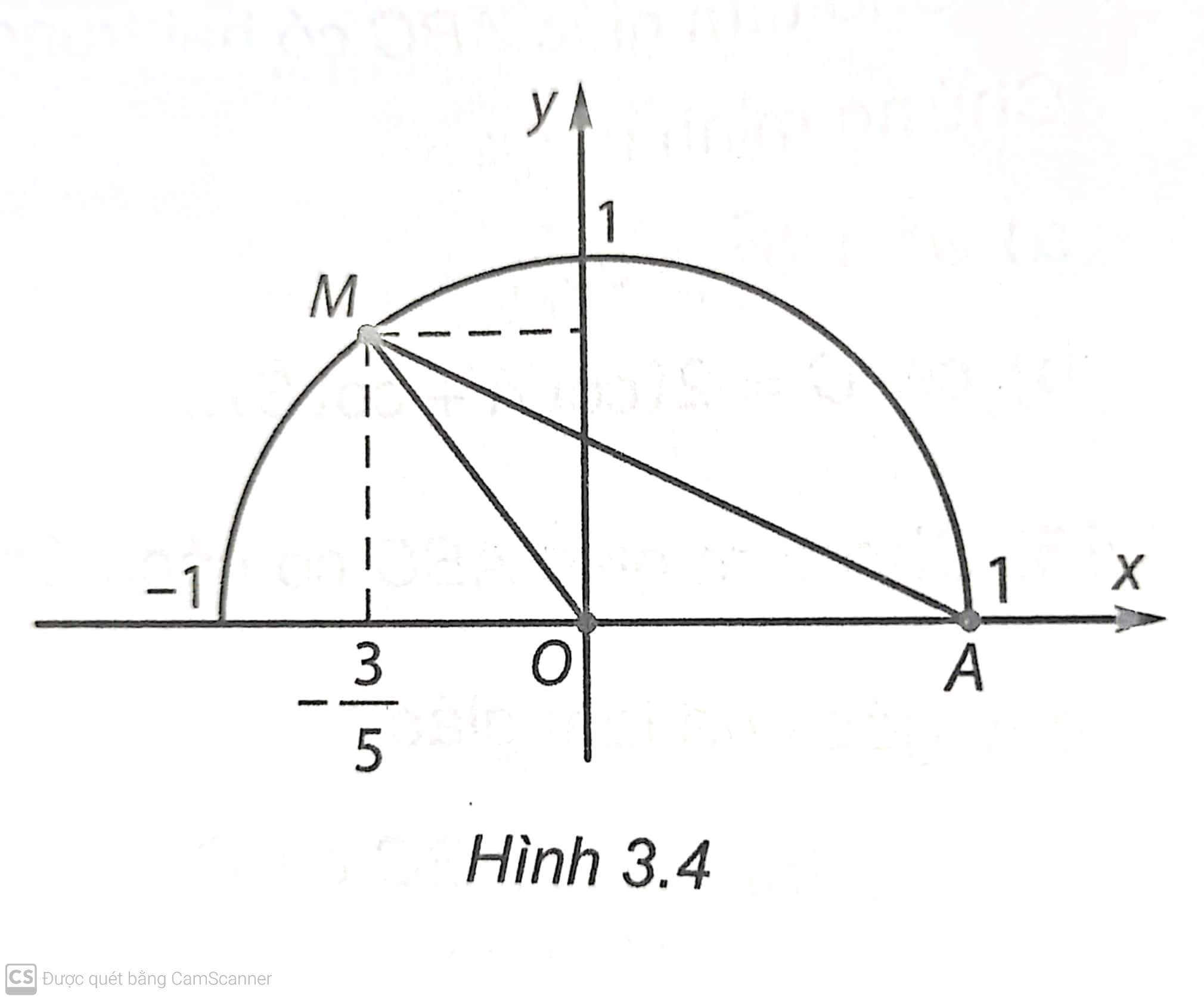
A. \(\frac{4}{5}.\)
B. \(\frac{2}{5}.\)
C. \(\frac{3}{5}.\)
D. \(\frac{3}{{10}}.\)
Bài 18 :
Trên mặt phẳng tọa độ \(Oxy,\) lấy điểm \(M\) thuộc nửa đường tròn đơn vị sao cho \(\widehat {xOM} = {150^ \circ }\)(H.3.5). \(N\) là điểm đối xứng với \(M\) qua trục tung. Diện tích của tam giác \(MAN\) bằng:
A. \(\frac{{\sqrt 3 }}{4}.\)
B. \(\frac{{\sqrt 3 }}{2}.\)
C. \(\sqrt 3 .\)
D. \(2\sqrt 3 .\)
Bài 19 :
Tính giá trị của \(T = 4\cos 60^\circ + 2\sin 135^\circ + 3\cot 120^\circ \).
Bài 20 :
Cho 00 < \(\alpha \) < 1800. Chọn câu trả lời đúng
A. cos\(\alpha \) < 0
B. sin\(\alpha \) > 0
C. tan\(\alpha \) < 0
D. cot\(\alpha \) > 0
Bài 21 :
Cho tam giác ABC cân tại A có \(\widehat A = 120^\circ \). Khi đó sin B bằng
-
A.
\(\frac{1}{2}\)
-
B.
\( - \frac{1}{2}\)
-
C.
\(\frac{{\sqrt 3 }}{2}\)
-
D.
\( - \frac{{\sqrt 3 }}{2}\)
Bài 22 :
Cho góc α với 0° < α < 180°. Tính giá trị của cosα, biết \(\tan \alpha = - 2\sqrt 2 \) .
-
A.
\( - \frac{1}{3}\)
-
B.
\(\frac{{2\sqrt 2 }}{3}\)
-
C.
\(\frac{1}{3}\)
-
D.
\(\frac{{\sqrt 2 }}{3}\)
Bài 23 :


















Danh sách bình luận