Số điểm một cầu thủ bóng rổ ghi được trong 20 trận đấu được cho ở bảng sau:

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng tứ phân vị của số liệu từ bảng tần số ghép nhóm trên.
a) Sắp xếp dãy số liệu theo thứ tự không giảm và tìm tứ phân vị.
b) Đếm và lập bảng.
c) Sử dụng công thức tính tứ phân vị.
a) Sắp xếp lại dãy số liệu theo thứ tự không giảm:

Tứ phân vị thứ nhất là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right) = \frac{1}{2}\left( {11 + 11} \right) = 11\)
Tứ phân vị thứ hai là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right) = \frac{1}{2}\left( {14 + 14} \right) = 14\)
Tứ phân vị thứ ba là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right) = \frac{1}{2}\left( {21 + 22} \right) = 21,5\)
b)

c) Do số trận đấu là số nguyên nên ta hiệu chỉnh như sau:

Tổng trận đấu là: \(n = 4 + 8 + 2 + 6 = 20\).
Gọi \({x_1};{x_2};...;{x_{20}}\) là điểm số của các trận đấu được xếp theo thứ tự không giảm.
Ta có:
\({x_1},...,{x_4} \in \begin{array}{*{20}{c}}{\left[ {5,5;10,5} \right)}\end{array};{x_5},...,{x_{12}} \in \begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array};{x_{13}},{x_{14}} \in \begin{array}{*{20}{c}}{\left[ {15,5;20,5} \right)}\end{array};{x_{15}},...,{x_{20}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{10}} + {x_{11}}} \right)\)
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_{10}},{x_{11}} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{2} - 4}}{8}.\left( {15,5 - 10,5} \right) = 14,25\)
• Tứ phân vị thứ nhất của dãy số liệu là: \(\frac{1}{2}\left( {{x_5} + {x_6}} \right)\).
Ta có: \(n = 20;{n_m} = 8;C = 4;{u_m} = 10,5;{u_{m + 1}} = 15,5\)
Do \({x_5},{x_6} \in \begin{array}{*{20}{c}}{\begin{array}{*{20}{c}}{\left[ {10,5;15,5} \right)}\end{array}}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{20}}{4} - 4}}{8}.\left( {15,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\).
Ta có: \(n = 20;{n_j} = 6;C = 4 + 8 + 2 = 14;{u_j} = 20,5;{u_{j + 1}} = 25,5\)
Do \({x_{15}},{x_{16}} \in \begin{array}{*{20}{c}}{\left[ {20,5;25,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 20,5 + \frac{{\frac{{3.20}}{4} - 14}}{6}.\left( {25,5 - 20,5} \right) \approx 21,3\)

Các bài tập cùng chuyên đề
Bài 1 :
Lương tháng của một số nhân viên một văn phòng được ghi lại như sau (đơn vị: triệu đồng):

Tìm tứ phân vị của dãy số liệu trên.
-
A.
\({Q_1} = 9;{Q_2} = 10,75;{Q_3} = 12,3\)
-
B.
\({Q_1} = 9;{Q_2} = 10,75;{Q_3} = 14,3\)
-
C.
\({Q_1} = 9;{Q_2} = 11,75;{Q_3} = 12,3\)
-
D.
\({Q_1} = 10;{Q_2} = 10,75;{Q_3} = 12,3\)
Bài 2 :
Thời gian truy cập Internet mỗi buổi tối của một số học sinh được cho trong bảng sau:

Hãy tìm tổng của tứ phân vị thứ nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) của mẫu số liệu ghép nhóm trên
-
A.
30,25.
-
B.
35,25.
-
C.
35,8.
-
D.
25,25.
Bài 3 :
Bảng dưới đây cho ta bảng tần số ghép nhóm số liệu thống kê cân nặng của 40 học sinh lớp 11A trong một trường trung học phổ thông (đơn vị: kilôgam).
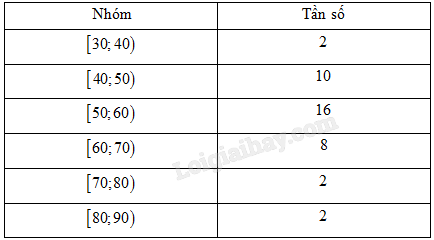
Hãy ước lượng các tứ phân vị của mẫu số liệu ghép số trên.
-
A.
\({Q_1} = 49\) (kg); \({Q_2} = 50\) (kg); \({Q_3} = 52,5\) (kg).
-
B.
\({Q_1} = 48\) (kg); \({Q_2} = 55\) (kg); \({Q_3} = 62,5\) (kg).
-
C.
\({Q_1} = 47\) (kg); \({Q_2} = 54\) (kg); \({Q_3} = 63,5\) (kg).
-
D.
\({Q_1} = 46\) (kg); \({Q_2} = 53\) (kg); \({Q_3} = 64,5\) (kg).
Bài 4 :
Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba cho mẫu số liệu ghép nhóm ở Luyện tập 2.
Bài 5 :
Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba cho mẫu số liệu ghép nhóm ở Luyện tập 2.
Bài 6 :
Với mẫu số liệu ghép nhóm cho trong HĐ2, hãy cho biết tứ phân vị nhất \({Q_1}\) và tứ phân vị thứ ba \({Q_3}\) thuộc nhóm nào.
Cho mẫu số liệu ghép nhóm như Bảng 3.2
Bài 7 :
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
[0;20) |
[20; 40) |
[40; 60) |
[60; 80) |
[80; 100) |
|
Số học sinh |
5 |
9 |
12 |
10 |
6 |
Nhóm chứa tứ phân vị thứ nhất là
A. \(\left[ {0;20} \right)\) C. \(\left[ {40;60} \right)\)
B. \(\left[ {20;40} \right)\) D. \(\left[ {60;80} \right)\)
Bài 8 :
Một bảng xếp hạng đã tính điểm chuẩn hóa cho chi số nghiên cứu của một số trường đại học ở Việt Nam và thu được kết quả sau:
Xác định điểm ngưỡng để đưa ra danh sách 25% trường đại học có chỉ số nghiên cứu tốt nhất Việt Nam.
Bài 9 :
Một phòng khám thống kê số bệnh nhân đến khám bệnh mỗi ngày trong tháng 4 năm 2022 ở bảng sau:

a) Hãy ước lượng các tử phân vị của mẫu số liệu ghép nhóm trên.
b) Quản lí phòng khám cho rằng có khoảng 25% số ngày khám có nhiều hơn 35 bệnh nhân đến khám. Nhận định trên có hợp lí không?
Bài 10 :
Một người thống kê lại thời gian thực hiện các cuộc gọi điện thoại của người đó trong 2 một tuần ở bảng sau:

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.
Bài 11 :
Thời gian luyện tập trong một ngày (tính theo giờ) của một số vận động viên được ghi lại ở bảng sau:

Huấn luyện viên muốn xác định nhóm gồm 25% các vận động viên có số giờ luyện tập cao nhất. Hỏi huấn luyện viên nên chọn các vận động viên có thời gian luyện tập từ bao nhiêu giờ trở lên vào nhóm này?
Bài 12 :
Lương tháng của một số nhân viên một văn phòng được ghi lại như sau (đơn vị: triệu đồng):

a) Tìm tứ phân vị của dãy số liệu trên.
b) Tổng hợp lại dãy số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng tứ phân vị của số liệu ở bảng tần số ghép nhóm trên.
Bài 13 :
Tứ phân vị thứ nhất của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
A. 7.
B. 7,6.
C. 8.
D. 8,6.
Bài 14 :
Tứ phân vị thứ ba của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?
A. 10.
B. 11.
C. 12.
D. 13.
Bài 15 :
Kiểm tra điện lượng của một số viên pin tiểu do một hãng sản xuất thu được kết quả sau:

Tìm tứ phân vị thứ nhất của mẫu số liệu.
Bài 16 :
Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tìm a sao cho có 25% số cầu thủ tham gia trận đấu chạy ít nhất a(km).
Bài 17 :
Thống kê số lần đi học muộn trong học kì của các bạn trong lớp, Nam thu được kết quả sau:

Tính các tứ phân vị của mẫu số liệu ghép nhóm và cho biết ý nghĩa của các kết quả thu được.
Bài 18 :
Số a thỏa mãn có 25% giá trị trong mẫu số liệu nhỏ hơn a và 75% giá trị trong mẫu số liệu lớn hơn a là
A. số trung bình
B. trung vị
C. tứ phân vị thứ nhất
D. tứ phân vị thứ ba.
Bài 19 :
Số a thỏa mãn có 75% giá trị trong mẫu số liệu nhỏ hơn a và 25% giá trị trong mẫu số liệu lớn hơn a là
A. số trung bình
B. trung vị
C. tứ phân vị thứ nhất
D. tứ phân vị thứ ba.
Bài 20 :
Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau:

Nhóm chứa tứ phân vị thứ nhất của mẫu số liệu là
A. \(\left[ {2;3,5} \right)\)
B. \(\left[ {3,5;\,\,5} \right)\)
C. \(\left[ {5;\,\,6,5} \right)\)
D. \(\left[ {6,5;\,\,8} \right)\)
Bài 21 :
Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau:

Nhóm chứa tứ phân vị thứ ba của mẫu số liệu là
A. \(\left[ {2;3,5} \right)\)
B. \(\left[ {3,5;\,\,5} \right)\)
C. \(\left[ {5;\,\,6,5} \right)\)
D. \(\left[ {6,5;\,\,8} \right)\)
Bài 22 :
Một trang báo điện tử thống kê thời gian người sử dụng đọc thông tin trên trang trong mỗi lần truy cập ở bảng sau:

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.
Bài 23 :
Người ta thống kê tốc độ của một số xe ô tô di chuyển qua một trạm kiểm soát trên đường cao tốc trong một khoảng thời gian ở bảng sau:

Hãy ước lượng các tứ phân vị của mẫu số liệu ghép nhóm trên.
Bài 24 :
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 156,25.
B. 157,5.
C. 156,38.
D. 157,54.
Bài 25 :
Trả lời các câu hỏi 6-10 dựa trên bảng số liệu về chiều cao của 100 học sinh một trường trung học phổ thông dưới đây.

Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần trăm) là
A. 160,52.
B. 161,52.
C. 161,14.
D. 162,25.
Bài 26 :
Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một số học sinh thu được kết quả sau:

Hãy cho biết ngưỡng thời gian để xác định 25% học sinh hoàn thành bài tập với thời gian lâu nhất.
Bài 27 :
Tìm tứ phân vị của mẫu số liệu trong bảng 1.
Bài 28 :
Giáo viên chủ nhiệm chia thời gian sử dụng Internet trong một ngày của 40 học sinh thành năm nhóm (đơn vị: phút) và lập bảng số ghép nhóm bao gồm cả tần số tích lũy như Bảng 12.
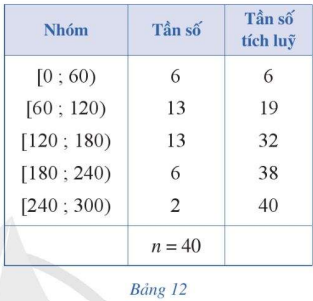
a) Tìm trung vị \({M_e}\) của mẫu số liệu ghép nhóm đó. Trung vị \({M_e}\) còn gọi là tứ phân vị thứ 2 \({Q_2}\) của mẫu số liệu trên.
b) Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{40}}{4} = 10\) có đúng không?
Tìm đầu mút trái \(s\), độ dài \(h\), tần số \({n_2}\) của nhóm 2; tần số tích lũy \(c{f_1}\) của nhóm 1
Sau đó, hãy tính giá trị \({Q_1}\) theo công thức sau: \({Q_1} = s + \left( {\frac{{10 - c{f_1}}}{{{n_2}}}} \right).h\)
Giá trị nói trên được gọi là tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu đã cho
c) Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.40}}{4} = 30\) có đúng không?
Bài 29 :
Để chuẩn bị cho đồ án tốt nghiệp, một sinh viên y khoa đã khảo sát huyết áp tối đa của một số bệnh nhân và lập được bảng tần số ghép nhóm sau:
|
Huyết áp |
Tần số |
|
[90;11) |
6 |
|
[110;130) |
20 |
|
[130;150) |
35 |
|
[150;170) |
45 |
|
[170;190) |
30 |
|
[190;210) |
16 |
Tìm tứ phân vị thứ ba của mẫu số liệu trên.
-
A.
155,9.
-
B.
136,9.
-
C.
156,7.
-
D.
175,3.
Bài 30 :
Người ta ghi lại tuổi thọ (năm) của 50 bình ắc quy của một hãng xe ô tô của cho kết quả như sau:
|
Tuổi thọ (năm) |
[2;2,5) |
[2,5;3) |
[3;3,5) |
[3,5;4) |
[4;4,5) |
[4,5;5) |
|
Tần số |
4 |
9 |
14 |
11 |
7 |
5 |
Tứ phân vị thứ nhất của mẫu số liệu trên gần với giá trị nào trong các giá trị sau đây?
-
A.
$2,92.$
-
B.
$2,97.$
-
C.
$2,75.$
-
D.
$2,95.$



















Danh sách bình luận