
Rút gọn hai phân số \(\dfrac{{91}}{{117}}\) và \(\dfrac{{182}}{{224}}\) thành phân số tối giản, sau đó quy đồng mẫu số ta được hai phân số lần lượt là:
-
A.
\(\dfrac{{112}}{{128}}\) và \(\dfrac{{102}}{{128}}\)
-
B.
\(\dfrac{{35}}{{45}}\) và \(\dfrac{{33}}{{45}}\)
-
C.
\(\dfrac{{80}}{{135}}\) và \(\dfrac{{105}}{{135}}\)
-
D.
\(\dfrac{{112}}{{144}}\) và \(\dfrac{{117}}{{144}}\)
Bước 1: Xét xem cả tử số và mẫu số của phân số đó cùng chia hết cho số tự nhiên nào (khác 1) không?
Bước 2: Chia cả tử số và mẫu số của phân số đó cho số tự nhiên vừa tìm được.
Bước 3: Cứ làm như thế cho đến khi tìm được phân số tối giản.
Bước 4: Sau khi tìm được phân số tối giản ta sẽ quy đồng mẫu số hai phân số đó.
Ta có:
\(\begin{array}{l}\dfrac{{91}}{{117}} = \dfrac{{91:13}}{{117:13}} = \dfrac{7}{9};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{182}}{{224}} = \dfrac{{182:14}}{{224:14}} = \dfrac{{13}}{{16}}\\MSC = 9 \times 16 = 144\\\dfrac{7}{9} = \dfrac{{7 \times 16}}{{9 \times 16}} = \dfrac{{112}}{{144}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{13}}{{16}} = \dfrac{{13 \times 9}}{{16 \times 9}} = \dfrac{{117}}{{144}}\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)
Rút gọn hai phân số \(\dfrac{{91}}{{117}}\) và \(\dfrac{{182}}{{224}}\) thành phân số tối giản sau đó quy đồng mẫu số ta được hai phân số lần lượt là \(\dfrac{{112}}{{144}}\)và \(\dfrac{{117}}{{144}}\).
Đáp án : D
Cần chú ý rút gọn hai phân số ban đầu cẩn thận, nếu rút gọn sai kéo theo bước quy đồng phân số sẽ sai.

Các bài tập cùng chuyên đề
Bài 1 :

Trong các cách viết phân số sau, cách viết nào sai?
-
A.
\(\dfrac{3}{5}\)
-
B.
\(\dfrac{{18}}{1}\)
-
C.
\(\dfrac{0}{7}\)
-
D.
\(\dfrac{5}{0}\)
Bài 2 :

Tử số của phân số \(\dfrac{{25}}{{37}}\) là
-
A.
$25$
-
B.
$26$
-
C.
\(37\)
-
D.
$23$
Bài 3 :

Phân số chỉ số ô vuông đã tô màu trong hình sau là:
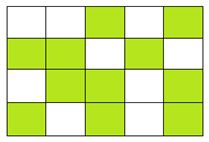
-
A.
\(\dfrac{9}{{11}}\)
-
B.
\(\dfrac{{11}}{{20}}\)
-
C.
\(\dfrac{{11}}{9}\)
-
D.
\(\dfrac{9}{{20}}\)
Bài 4 :

Thương của phép chia \(9:14\) được viết dưới dạng phân số là:
-
A.
\(\dfrac{{14}}{9}\)
-
B.
\(\dfrac{9}{1}\)
-
C.
\(\dfrac{9}{{14}}\)
-
D.
Không viết được
Bài 5 :

Điền số thích hợp vào chỗ chấm:
\(1 = \dfrac{{...}}{{99}}\)
-
A.
\(100\)
-
B.
\(98\)
-
C.
$97$
-
D.
$99$
Bài 6 :

Chọn số thích hợp để điền vào chỗ chấm: \(\dfrac{2}{3} = \dfrac{8}{{...}}\)
-
A.
$1$
-
B.
$12$
-
C.
$15$
-
D.
$24$
Bài 7 :
.jpg) Trong các phân số sau, phân số nào bằng với phân số \(\dfrac{4}{7}\)?
Trong các phân số sau, phân số nào bằng với phân số \(\dfrac{4}{7}\)?
Bài 8 :

Rút gọn phân số \(\dfrac{{15}}{{36}}\) thành phân số tối giản ta được phân số nào sau đây?
-
A.
\(\dfrac{5}{6}\)
-
B.
\(\dfrac{5}{{12}}\)
-
C.
\(\dfrac{3}{{12}}\)
-
D.
\(\dfrac{5}{{15}}\)
Bài 9 :
 Chọn số thích hợp để điền vào chỗ chấm: \(\dfrac{{637}}{{741}} = \dfrac{{49}}{{...}}\)
Chọn số thích hợp để điền vào chỗ chấm: \(\dfrac{{637}}{{741}} = \dfrac{{49}}{{...}}\)
-
A.
\(56\)
-
B.
$67$
-
C.
$57$
-
D.
$75$
Bài 10 :

Con hãy chọn đáp án đúng nhất:
Trong hai phân số có cùng mẫu số thì:
-
A.
Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
-
B.
Phân số nào có tử số bé hơn thì phân số đó bé hơn.
-
C.
Nếu tử số bằng nhau thì hai phân số đó bằng nhau.
-
D.
Tất cả các đáp án trên đều đúng.
Bài 11 :

Để \(\dfrac{a}{b} < \dfrac{a}{c}\,\,\,\)( \(b\) khác \(0\), \(c\) khác \(0\)) thì ta cần có thêm điều kiện gì của \(b\) và \(c\)?
-
A.
\(b = c\)
-
B.
\(b > c\)
-
C.
\(b < c\)
-
D.
A và C đều đúng
Bài 12 :
.jpg)
Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{5}{9} \cdot \cdot \cdot \dfrac{7}{9}\)
Bài 13 :
 Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với \(1\)?
Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với \(1\)?
-
A.
Khi hai phân số đều bé hơn \(1\)
-
B.
Khi hai phân số đều lớn hơn \(1\)
-
C.
Khi một phân số bé hơn \(1\) và một phân số lớn hơn \(1\)
-
D.
Khi hai phân số đều bằng \(1\)
Bài 14 :

Khi nào ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian?
-
A.
Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai.
-
B.
Khi tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu số của phân số thứ hai.
-
C.
Cả A và B đều sai.
-
D.
Cả A và B đều đúng.
Bài 15 :

Phần bù với \(1\) của phân số \(\dfrac{{97}}{{98}}\) là:
-
A.
\(1\)
-
B.
\(\dfrac{1}{{98}}\)
-
C.
\(\dfrac{{98}}{{97}}\)
-
D.
\(\dfrac{{195}}{{98}}\)
Bài 16 :

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{4}{{15}} \cdot \cdot \cdot \dfrac{4}{{11}}\)
Bài 17 :

Chọn phân số lớn hơn trong hai phân số sau:
Bài 18 :

Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{3}{4} \cdot \cdot \cdot \dfrac{2}{5}\)
Bài 19 :

Kéo thả dấu thích hợp vào ô trống:
Bài 20 :

Chọn phân số bé hơn trong hai phân số sau:
Bài 21 :

Rút gọn rồi so sánh hai phân số: \(\dfrac{{215}}{{135}}\) và \(\dfrac{{207}}{{81}}\)
Con hãy chọn phân số lớn hơn nhé.
Bài 22 :

Sắp xếp các phân số sau theo thứ tự từ bé đến lớn: \(\dfrac{4}{5};\,\,\dfrac{{33}}{{35}};\,\,\dfrac{{11}}{{14}}\)
Bài 23 :

Phần hơn với \(1\) của phân số \(\dfrac{{145}}{{141}}\) là:
Bài 24 :
 Khi so sánh hai phân số \(\dfrac{{51}}{{72}}\) và \(\dfrac{{63}}{{67}}\) ta có thể chọn phân số trung gian là :
Khi so sánh hai phân số \(\dfrac{{51}}{{72}}\) và \(\dfrac{{63}}{{67}}\) ta có thể chọn phân số trung gian là :
Bài 25 :
.gif)
Kéo thả dấu thích hợp vào ô trống:
Bài 26 :
.jpg)
Chọn phân số lớn hơn trong hai phân số sau:
Bài 27 :
.jpg)
Kéo thả dấu thích hợp vào ô trống:
Bài 28 :
.jpg)
Chọn dấu thích hợp để điền vào chỗ chấm:
\(\dfrac{{273}}{{274}} \cdot \cdot \cdot \dfrac{{546}}{{548}}\)
Bài 29 :
.jpg)
Kéo thả dấu thích hợp vào ô trống
Bài 30 :

Điền phân số thích hợp vào ô trống.


















Danh sách bình luận