Một loại vi khuẩn được nuôi cấy trong phòng thí nghiệm, cứ mỗi phút số lượng lại tăng lên gấp đôi số lượng đang có. Từ một vi khuẩn ban đầu, hãy tính tổng số vi khuẩn có trong ống nghiệm sau 20 phút.
Cấp số nhân có số hạng đầu \({u_1}\) và công bội \(q\) thì số hạng tổng quát là: \({u_n} = {u_1}.{q^{n - 1}},n \ge 2\).
Số lượng vi khuẩn trong ống nghiệm sau \(n\) phút là một cấp số nhân có số hạng đầu \({u_1} = 1\) và công bội \(q = 2\).
Số lượng vi khuẩn ban đầu là \({u_1} = 1\).
Số lượng vi khuẩn sau 1 phút là \({u_2}\).
Số lượng vi khuẩn sau 2 phút là \({u_3}\).
...
Số lượng vi khuẩn trong ống nghiệm sau 20 phút là:
\({u_{21}} = {u_1}.{q^{n - 1}} = {1.2^{21 - 1}} = 1048576\) (vi khuẩn).
Lỗi sai thường gặp: Tính \({u_{20}}\).
Sau mỗi phút, số lượng vi khuẩn gấp đôi số lượng đang có. Giả sử hiện tại số vi khuẩn là a thì sau 1 phút, số vi khuẩn sẽ là 2a, không phải a + 2a. Vì vậy ta không tính tổng \(S_n\).

Các bài tập cùng chuyên đề
Bài 1 :
Với giá trị x; y nào dưới đây thì các số hạng lần lượt là \( - 2;x; - 18;y\) theo thứ tự đó lập thành một cấp số nhân?
-
A.
\(\left\{ \begin{array}{l}x = 6\\y = - 54\end{array} \right.\)
-
B.
\(\left\{ \begin{array}{l}x = - 10\\y = - 26\end{array} \right.\)
-
C.
\(\left\{ \begin{array}{l}x = - 6\\y = - 54\end{array} \right.\)
-
D.
\(\left\{ \begin{array}{l}x = - 6\\y = 54\end{array} \right.\)
Bài 2 :
Một cấp số nhân có 6 số hạng với công bội bằng 2 và tổng số các số hạng bằng 189. Tìm số hạng cuối \({u_6}\) của cấp số nhân đã cho.
-
A.
32
-
B.
104
-
C.
48
-
D.
96
Bài 3 :
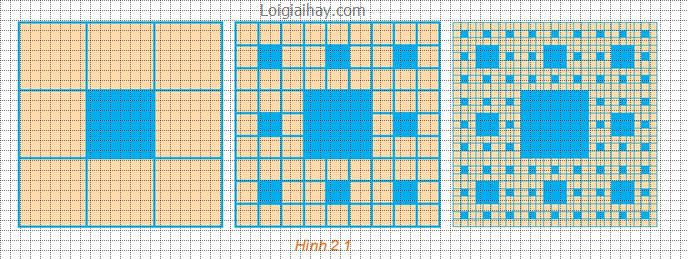
Một hình vuông màu vàng có cạnh 1 đơn vị dài được chia thành chín hình vuông nhỏ hơn và hình vuông ở chính giữa được tô màu xanh như Hình 2.1. Mỗi hình vuông màu vàng nhỏ hơn lại được chia thành chín hình vuông con, và mỗi hình vuông con ở chính giữa lại được tô màu xanh. Nếu quá trình này được tiếp tục lặp lại năm lần thì tổng diện tích các hình vuông được tô màu xanh bao nhiêu?
Bài 4 :
Cho cấp số nhân \(\left( {{u_n}} \right)\) với \({u_1} = 3;{u_3} = \frac{{27}}{4}\)
a) Tìm công bội q và viết năm số hạng đầu của cấp số nhân trên
b) Tính tổng 10 số hạng đầu của cấp số nhân trên
Bài 5 :
Một tỉnh có 2 triệu dân vào năm 2020 với tỉ lệ tăng dân số là 1%/năm. Gọi \({u_n}\) là số dân của tỉnh đó sau n năm. Giả sử tỉ lệ tăng dân số là không đổi.
a) Viết công thức tính số dân của tỉnh đó sau n năm kể từ năm 2020.
b) Tính số dân của tỉnh đó sau 10 năm kể từ năm 2020.
Bài 6 :
Một gia đình mua một chiếc ô tô giá 800 triệu đồng. Trung bình sau mỗi năm sử dụng, giá trị của ô tô giảm đi 4% (so với năm trước đó).
a) Viết công thức tính giá trị của ô tô sau 1 năm, 2 năm sử dụng
b) Viết công thức tính giá trị của ô tô sau n năm sử dụng
c) Sau 10 năm, giá trị của ô tô ước tính còn bao nhiêu triệu đồng?
Bài 7 :
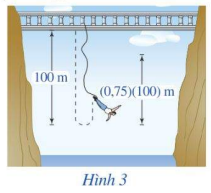
Một người nhảy bungee (một trò chơi mạo hiểm mà người chơi nhảy từ một nơi có địa thế cao xuống với dây đai an toàn buộc xung quanh người) từ một cây cầu và căng một sợi dây dài 100m. Giả sử sau mỗi lần rơi xuống, người nhảy được kéo lên một quãng đường có độ dài bằng 75% so với lần rơi trước đó và lại bị rơi xuống đúng bằng quãng đường vừa được kéo lên (Hình 3). Tính tổng quãng đường người đó đi được sau 10 lần rơi xuống và lại được kéo lên, tính từ lúc bắt đầu nhảy (làm tròn kết quả đến hàng đơn vị).
Bài 8 :
Cho dãy số \(\left( {{u_n}} \right)\) được xác định bởi: \({u_1} = \frac{1}{3}\) và \({u_n} = 3{u_{n - 1}}\) với mọi \(n \ge 2\). Số hạng thứ năm của dãy số \(\left( {{u_n}} \right)\) là:
A.27
B.9
C.81
D.243
Bài 9 :
Một cái tháp có 11 tầng. Diện tích của mặt sàn tầng 2 bằng nửa diện tích của mặt đáy tháp và diện tích của mặt sàn mỗi tầng bằng nửa diện tích của mặt sàn mỗi tầng ngay bên dưới. Biết mặt đáy tháp có diện tích là 12 288 \({m^2}\). Tính diện tích của mặt sàn tầng trên cùng của tháp theo đơn vị mét vuông.
Bài 10 :
Một khay nước có nhiệt độ \(23^\circ C\) được đặt vào ngăn đá của tủ lạnh. Biết sau mỗi giờ, nhiệt độ của nước giảm 20% so với nhiệt độ của giờ trước đó. Tính nhiệt độ của khay nước đó sau 6 giờ.
Bài 11 :
Một hình vuông \({C_1}\) có cạnh bằng 4. Người ta chia mỗi cạnh hình vuông thàng bốn phần bằng nhau và nối các điểm chia một cách thích hợp để có hình vuông \({C_2}\) (Hình 4). Từ hình vuông \({C_2}\) lại làm tiếp tục như trên để có hình vuông \({C_3}\). Cứ tiếp tục quá trình như trên, ta nhận được dãy các hình vuông \({C_1},{C_2},{C_3},..,{C_n},...\). Gọi \({a_n}\) là độ dài cạnh hình vuông \({C_n}\). Chứng minh rằng dãy số \(\left( {{a_n}} \right)\) là cấp số nhân.

Bài 12 :
Ông An vay ngân hàng 1 tỉ đồng, với lãi suất 12%/năm. Ông đã trả nợ theo cách: Bắt đầu từ tháng thứ nhất sau khi vay, cuối mỗi tháng ông trả ngân hàng cùng số tiền là a (đồng) và đã trả hết nợ sau đúng 2 năm kể từ ngày vay. Hỏi số tiền mỗi tháng mà ông An phải trả là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn)?
Bài 13 :
Giả sử một thành phố có dân số năm 2022 là khoảng 2,1 triệu người và tốc độ gia tăng dân số trung bình mỗi năm là 0,75%.
a) Dự đoán dân số của thành phố đó vào năm 2032.
b) Nếu tốc độ gia tăng dân số vẫn giữ nguyên như trên thì ước tính vào năm nào dân số của thành phố đó sẽ tăng gấp đôi so với năm 2022.
Bài 14 :
Trong trò chơi mạo hiểm nhảy bungee, mỗi lần nhảy, người chơi sẽ được dây an toàn có tính đàn hồi kéo nảy ngược lên 60% chiều sâu của cú nhảy. Một người chơi bungee thực hiện cú nhảy đầu tiên có độ cao nảy ngược lên là 9 m.
a) Tính độ cao nảy ngược lên của người đó ở lần nảy thứ ba.
b) Tính tổng các độ cao nảy ngược lên của người đó trong 5 lần nảy đầu.
Bài 15 :
Một cây đàn organ có tần số âm thanh các phím liên tiếp tạo thành một cấp số nhân. Cho biết tần số phím La Trung là 400 Hz và tần số của phím La Cao cao hơn 12 phím là 800 Hz (nguồn: https:// vi.wikipedia.org/wiki/Organ). Tìm công bội của cấp số nhân nói trên (làm tròn kết quả đến hàng phần nghìn).
Bài 16 :
Dân số Việt Nam năm 2020 là khoảng 97,6 triệu người (theo Niên giám thống kê năm 2020). Nếu trung bình mỗi năm tăng 1,14% thì ước tính dân số Việt Nam năm 2040 là khoảng bao nhiêu người (làm tròn kết quả đến hàng trăm nghìn)?
Bài 17 :
Tìm x sao cho \(x,x + 2,x + 3\) là ba số hạng liên tiếp của một cấp số nhân.
Bài 18 :
Để tích lũy tiền cho việc học đại học của con gái, cô Hoa quyết định hằng tháng bỏ ra 500 nghìn đồng vào tài khoản tiết kiệm, được trả lãi 0,5% cộng dồn hằng tháng. Cô bắt đầu chương trình tích lũy này khi con gái cô tròn 3 tuổi. Cô ấy sẽ tích lũy được bao nhiêu tiền vào thời điểm gửi khoản tiền thứ 180? Lúc này con gái cô Hoa bao nhiêu tuổi?
Bài 19 :
Các cạnh của hình vuông ban đầu có chiều dài 16cm. Một hình vuông mới được hình thành bằng cách nối các điểm giữa của các cạnh của hình vuông ban đầu và hai trong số các hình tam giác kết quả được tô màu (hình vẽ dưới). Nếu quá trình này được lặp lại năm lần nữa, hãy xác định tổng diện tích của vùng được tô màu.
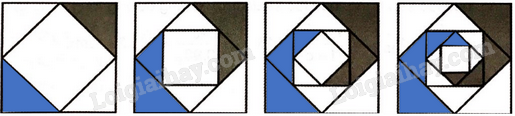
Bài 20 :
Các cạnh của hình vuông ban đầu có chiều dài 16cm. Một hình vuông mới được hình thành bằng cách nối các điểm giữa của các cạnh của hình vuông ban đầu và hai trong số các hình tam giác kết quả được tô màu (hình vẽ dưới). Nếu quá trình này được lặp lại năm lần nữa, hãy xác định tổng diện tích của vùng được tô màu.

Bài 21 :
Nếu p, m và q lập thành một cấp số nhân thì dễ thấy \({m^2} = p.q.\) Số m được gọi là trung bình nhân của p và q. Cho hai số q và q, nếu ta tìm được k số khác \({m_1},{m_2},...,{m_k}\) sao cho \(p,{m_1},{m_2},...,{m_k},q\) lập thành một cấp số nhân, thì chúng ta nói rằng đã “chèn k trung bình nhân vào giữa p và q”. Hãy:
a) Chèn hai trung bình nhân vào giữa 3 và 24;
b) Chèn ba trung bình nhân vào giữa 2,25 và 576.
Bài 22 :
Một chiếc máy photocopy lúc mới mua là 50 triệu đồng. Biết rằng giá trị của nó sau mỗi năm sử dụng chỉ còn 75% giá trị trong năm liền trước đó. Tính giá trị còn lại của chiếc máy photocopy đó sau mỗi năm, trong khoảng thời gian 5 năm kể từ khi mua.
Bài 23 :
Bác An gửi tiết kiệm 200 triệu đồng kì hạn 3 tháng, với lãi suất 3% một năm. Số tiền (triệu đồng) cả vốn lẫn lãi mà bác An nhận được sau n quý (mỗi quý là 3 tháng) sẽ là \({A_n} = 200{\left( {1 + \frac{{0,03}}{4}} \right)^n},n = 0,1,2,...\)
a) Viết ba số hạng đầu của dãy số.
b) Tìm số tiền bác An nhận được sau 2 năm.
Bài 24 :
Viết bốn số hạng xen giữa các số 1 và \( - 243\) để được một cấp số nhân có 6 số hạng. Bốn số hạng đó lần lượt là:
A. \( - 3; - 9; - 27; - 81\)
B. \(3; - 9;27; - 81\)
C. \(3;9;27;81\)
D. \( - 3;9; - 27;81\)
Bài 25 :
cấp số nhân \(\left( {{u_n}} \right)\), biết \({u_2}.{u_6} = 64\). Giá trị của \({u_3}.{u_5}\) là:
A. \( - 8\)
B. \( - 64\)
C. 64
D. 8
Bài 26 :
Cho hình vuông \({C_1}\) có cạnh bằng 1. Gọi \({C_2}\) là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông \({C_1}\); \({C_3}\) là hình vuông có các đỉnh là trung điểm các cạnh của hình vuông \({C_2}\); … Cứ tiếp tục quá trình như trên, ta được dãy các hình vuông \({C_1}\); \({C_2}\); \({C_3}\); … ; \({C_n}\); … Diện tích của hình vuông \({C_{2023}}\) là:
A. \(\frac{1}{{{2^{2022}}}}\)
B. \(\frac{1}{{{2^{2023}}}}\)
C. \(\frac{1}{{{2^{1011}}}}\)
D. \(\frac{1}{{{2^{1012}}}}\)
Bài 27 :
Tìm \(x\) để ba số \(2x - 3\), \(x\), \(2x + 3\) theo thứ tự lập thành một cấp số nhân.
Bài 28 :
Tìm số hạng đầu và công bội của cấp số nhân \(\left( {{u_n}} \right)\), biết:
a) \(\left\{ \begin{array}{l}{u_3} = 16\\{u_2} + {u_4} = 40\end{array} \right.\)
b) \(\left\{ \begin{array}{l}{u_1} + {u_6} = 244\\{u_2}.{u_5} = 243\end{array} \right.\)
c) \(\left\{ \begin{array}{l}{u_1} + {u_2} + {u_3} = 13\\{u_4} + {u_5} + {u_6} = 351\end{array} \right.\)
Bài 29 :
Cho cấp số nhân \(\left( {{u_n}} \right)\) biết \({u_1} = - 1\), \(q = 3\).
a) Tính tổng 10 số hạng đầu của cấp số nhân đó.
b) Giả sử tổng \(m\) số hạng đầu của \(\left( {{u_n}} \right)\) bằng \( - 364\). Tìm \(m\)
c) Tính tổng \(S = \frac{1}{{{u_1}}} + \frac{1}{{{u_2}}} + \frac{1}{{{u_3}}} + \frac{1}{{{u_4}}} + \frac{1}{{{u_5}}}\).
Bài 30 :
Cho dãy số \(\left( {{u_n}} \right)\) biết \({u_1} = 1\), \({u_n} = \frac{1}{3}{u_{n - 1}} + 1\) với \(n \in {\mathbb{N}^*}\), \(n \ge 2\). Đặt \({v_n} = {u_n} - \frac{3}{2}\) với \(n \in {\mathbb{N}^*}\).
a) Chứng minh rằng dãy số \(\left( {{v_n}} \right)\) là cấp số nhân. Tìm số hạng đầu, công bội của cấp số nhân đó.
b) Tìm công thức số hạng tổng quát của \(\left( {{u_n}} \right)\), \(\left( {{v_n}} \right)\).
c) Tính tổng \(S = {u_1} + {u_2} + {u_3} + ... + {u_{10}}\).


















Danh sách bình luận