Đề bài

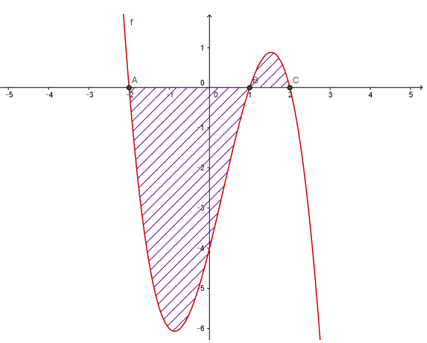
Cho đồ thị hàm số $y = f\left( x \right)$ như hình vẽ dưới đây. Diện tích $S$ của hình phẳng (phần gạch chéo) được xác định bởi

• A. \(S = \int_{ - 2}^2 {f(x)dx} \)
• B. \(S = \int_1^{ - 2} {f(x)dx}  + \int_1^2 {f(x)dx}  \)
• C. \(S = \int_{ - 2}^1 {f(x)dx}  + \int_1^2 {f(x)dx} \)
• D. \(S = \int_{ - 2}^1 {f(x)dx}  - \int_1^2 {f(x)dx}   \)

Phương pháp giải

- Bước 1: Giải phương trình \(f\left( x \right) = g\left( x \right)\) tìm nghiệm.

- Bước 2: Phá dấu giá trị tuyệt đối của biểu thức \(\left| {f\left( x \right) - g\left( x \right)} \right|\)

- Bước 3: Tính diện tích hình phẳng theo công thức tích phân \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \)

Lời giải của GV Loigiaihay.com

Nhận thấy phần đồ thị chia làm 2 phần, chú ý đến cận của từng phần.

Phần 1 có cận từ $ - 2$  đến $1$  nhưng trong \(\left( { - 1;2} \right)\), đồ thị hàm số nằm phía dưới trục hoành.

Phần 2 có cận từ 1 đến 2 và đồ thị hàm số nằm phía trên trục hoành.

Vậy \(S = \int_{-2}^{ 1} ({-f(x))dx}  + \int_1^2 {f(x)dx} = \int_1^{ - 2} {f(x)dx}  + \int_1^2 {f(x)dx}  \)

Đáp án : B

Chú ý

Một số em sẽ chọn nhầm đáp án A vì không nhớ kĩ công thức tính diện tích.