Cho hình hộp chữ nhật với kích thước như Hình 3a. Hình hộp này được cắt đi một nửa để có hình lăng trụ đứng như ở Hình 3b
a) Tính thể tích của hình hộp chữ nhật.
b) Dự đoán thể tích của hình lăng trụ đứng tam giác dựa vào thể tích hình hộp chữ nhật ở câu a.
c) Gọi Sđáy là diện tích mặt đáy và h là chiều cao của hình lăng trụ tam giác. Hãy tính Sđáy . h
d) So sánh Sđáy . h và kết quả dự đoán ở câu b.
Thể tích của hình hộp chữ nhật có chiều dài đáy a, chiều rộng b, chiều cao c là: V = a.b.c
Diện tích hình chữ nhật có chiều dài a, chiều rộng b là: S = a.b
a) Thể tích của hình hộp chữ nhật là: V = 4.3.6 = 72 (cm3)
b) Vì hình hộp cắt đi một nửa thì được hình lăng trụ đứng nên dự đoán thể tích của hình lăng trụ đứng tam giác bằng một nửa thể tích hình hộp chữ nhật ở câu a.
c) Sđáy = 4.3:2 = 6 (cm2)
Sđáy . h = 6.6 = 36 (cm3)
d) Sđáy . h = 36 = \(\frac {1}{2}\). 72 = \(\frac {1}{2}\).Vhình hộp
Vậy Sđáy . h và kết quả dự đoán ở câu b là như nhau.

Các bài tập cùng chuyên đề
Bài 1 :
Tính thể tích hình lăng trụ đứng tứ giác có đáy là hình thang với kích thước cho trong Hình 5
Bài 2 :
Để thi công một con dốc, người ta đúc một khối bê tông hình lăng trụ đứng tam giác có kích thước như Hình 8. Hãy tính thể tích khối bê tông.
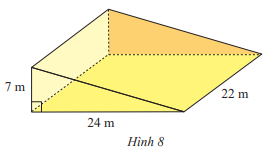
Bài 3 :
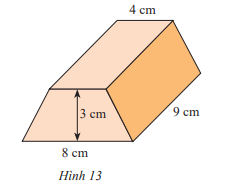
Tính thể tích hình lăng trụ đứng có đáy là hình thang cân với kích thước như hình 13
Bài 4 :
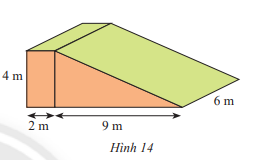
Để làm đường dẫn bắc ngang một con đê, người ta đúc một khối bê tông có kích thước như Hình 14. Tính chi phí để đúc khối bê tông đó, biết rằng chi phí để đúc 1 m3 bê tông là 1,2 triệu đồng.
Bài 5 :
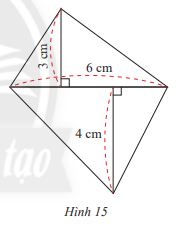
Một hình lăng trụ đứng tứ giác có kích thước đáy như hình 15, biết chiều cao của lăng trụ là 7 cm. Tính thể tích của hình lăng trụ.
Bài 6 :
Hình 34 mô tả một xe chở hai bánh mà thùng chứa của nó có dạng lăng trụ đứng tam giác với các kích thước cho trên hình. Hỏi thùng chứa của xe chở hai bánh đó có thể tích bằng bao nhiêu?
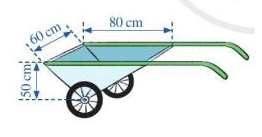
Bài 7 :
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Hình lăng trụ có chiều cao AA' = 3 cm. Thể tích của hình lăng trụ đó là:
-
A.
V = 9 cm3;
-
B.
V = 18 cm3;
-
C.
V = 24 cm3;
-
D.
V = 36 cm3.
Bài 8 :
Một chiếc hộp hình hộp chữ nhật có đáy là hình vuông cạnh 3 cm, chiều cao 7 cm. Nam cắt chiếc hộp thành hai hình lăng trụ đứng tứ giác với kích thước các đoạn cắt trên như Hình 6. Tính thể tích của hai hình lăng trụ đứng tứ giác sau khi cắt.
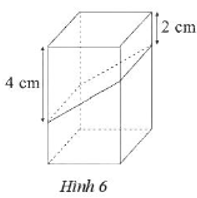
Bài 9 :
Mô hình một ngôi nhà có kích thước như Hình 7. Tính thể tích của mô hình ngôi nhà.
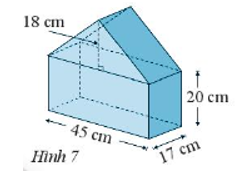
Bài 10 :
Một chi tiết máy bằng thép hình lăng trụ đứng tứ giác có đáy là một hình thoi có độ dài hai đường chéo là 16 cm và 18 cm, chiều cao 10 cm. Người ta khoét một lỗ hình hộp chữ nhật (Hình 9) có kích thước hai cạnh đáy là 2 cm và 6 cm. Tính thể tích còn lại của khối thép.
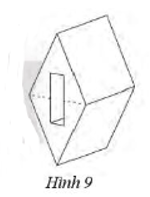
Bài 11 :
Tính thể tích của một hình lăng trụ đứng đáy là một tứ giác như Hình 10, có độ dài AC = 5 m, BM = DN = 3 m, chiều cao của lăng trụ 7 m.
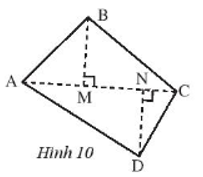
Bài 12 :
Một khối bê tông hình lăng trụ đứng tam giác, bên trong khoét một cái lỗ có kích thước như Hình 12 (đơn vị dm). Tính thể tích của khối bê tông.
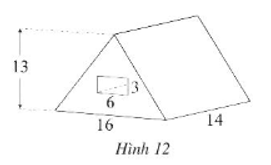
Bài 13 :
Thùng đựng của một máy cắt cỏ có dạng lăng trụ đứng tam giác. Hãy tính thể tích của thùng.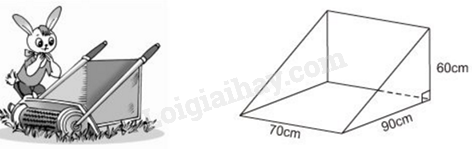
Bài 14 :
Một nhà kho có dạng hình lăng trụ đứng, đáy là hình thang vuông. Chiều cao của hình lăng trụ đứng (là chiều dài của nhà kho) bằng 6 m. Đường cao của đáy (là chiều rộng của nhà kho) bằng 5 m. Các cạnh đáy của hình thang vuông dài 3 m và 4 m. Tính thể tích của nhà kho.
Bài 15 :
Một khối kim loại có dạng hình lăng trụ đứng đáy tam giác vuông có kích thước hai cạnh góc vuông là 3 cm, 4 cm, cạnh huyền 5 cm. Người ta khoét một lỗ hình lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 2 cm, 1,5 cm, cạnh huyền 2,5 cm (Hình 2). Tính thể tích của khối kim loại (không tính cái lỗ).
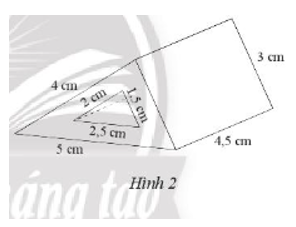
Bài 16 :
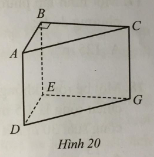
Cho hình lăng trụ đứng tam giác ABC.DEG có đáy là tam giác ABC vuông tại B với cạnh đáy \(AB = 2{\rm{ cm}}\) và cạnh bên \(AD = 5{\rm{ cm}}\) (Hình 20). Tính độ dài cạnh BC, biết thể tích của hình lăng trụ đó bằng 25 cm3.
Bài 17 :
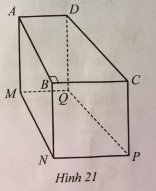
Cho hình lăng trụ đứng tứ giác ABCD.MNPQ có đáy là hình thang vuông ABCD vuông tại B (AD song song với BC) với \(AB = 20{\rm{ cm}}\), \(AD = 11{\rm{ cm}}\), \(BC = 15{\rm{ cm}}\) (Hình 21).
a) Tính tỉ số giữa thể tích của hình lăng trụ đứng tam giác ABC.MNP và thể tích của hình lăng trụ đứng tứ giác ABCD.MNPQ.
b) Tính tỉ số phần trăm giữa thể tích của hình lăng trụ đứng tam giác ABD.MNQ và thể tích của hình lăng trụ đứng tam giác BCD.NPQ.
c) So sánh thể tích của hai hình lăng trụ đứng tam giác ABD.MNQ và ACD.MPQ.
Bài 18 :
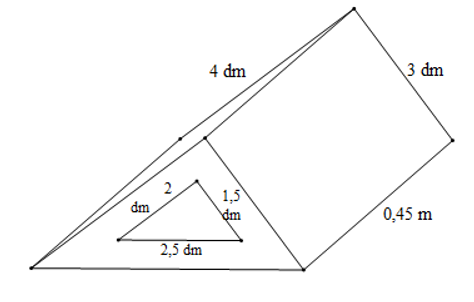
Một khối gỗ có dạng hình lăng trụ đứng đáy là tam giác vuông có kích thước thước hai cạnh góc vuông là 3 dm; 4 dm, cạnh huyền (cạnh đối diện với góc vuông) là 0,5 m. Người ta khoét một lỗ lăng trụ đứng đáy tam giác vuông hai cạnh góc vuông có kích thước là 1,5 dm; 2 dm; cạnh huyền 2,5 dm. Biết khối gỗ dài 0,45 m (hình vẽ). Tính thể tích của khối gỗ.
Bài 19 :
Người ta đào một đoạn mương dài 20 m, sâu 1,5 m. Bề mặt của mương rộng 1,8 m và đáy mương rộng 1,2 m. Tính thể tích khối đất phải đào.
Bài 20 :
Một chiếc khay đựng linh kiện bằng nhựa, có dạng hình lăng trụ đứng, đáy là hình thang vuông với độ dài hai cạnh đáy là 30 cm, 40 cm và các kích thước như hình 10.29. Tính thể tích của khay.
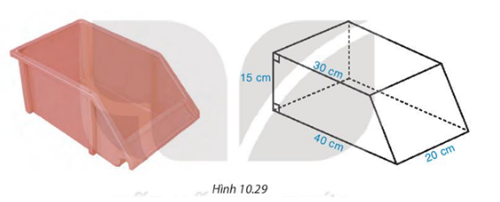
Bài 21 :
Thùng một chiếc máy nông nghiệp có dạng hình lăng trụ đứng tứ giác như hình 10.34. Đáy của hình lăng trụ đứng này (mặt bên của thùng) là một hình thang vuông có độ dài đáy lớn 3 m, đáy nhỏ 1,5 m. Hỏi thùng có dung tích bao nhiêu mét khối?
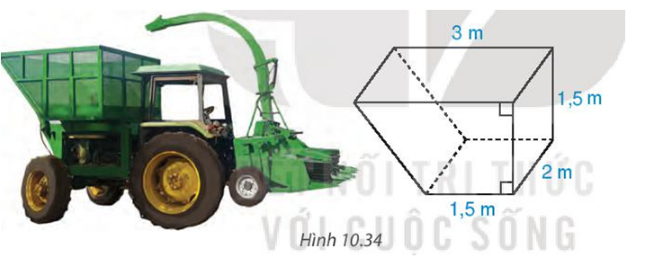
Bài 22 :
Một hình gồm hai lăng trụ đứng ghép lại với các kích thước như ở hình 10.35. Tính thể tích hình ghép.
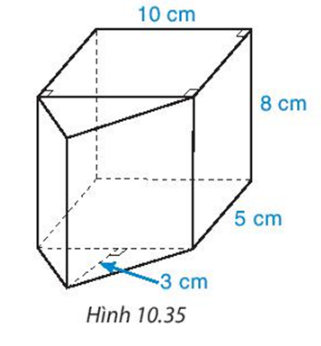
Bài 23 :
Người ta đào một đoạn mương có dạng hình lăng trụ đứng tứ giác như hình 10.42. Biết mương có chiều dài 20m , sâu 1,5 m, bề mặt có chiều rộng 1,8 m và đáy mương rộng 1,2 m. Tính thể tích đất phải đào lên.
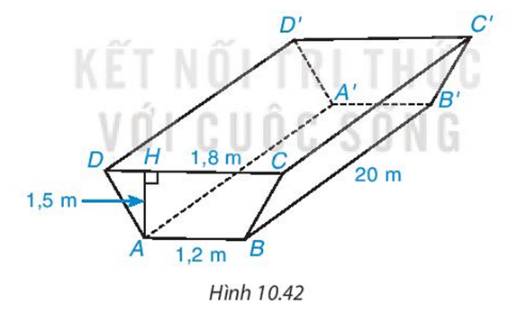
Bài 24 :
Cho hình lăng trụ đứng tam giác ABC.DEF như hình vẽ.
Biết AB = 4cm, AC = 3cm, BE = 6cm. Thể tích hình lăng trụ đó bằng
-
A.
\(20c{m^3}\).
-
B.
\(36c{m^3}\).
-
C.
\(26c{m^3}\).
-
D.
\(9c{m^3}\).
Bài 25 :
Tính thể tích hình lăng trụ đứng tam giác trong Hình 10.8.
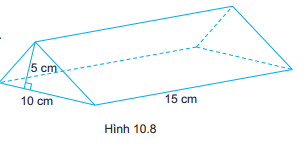
Bài 26 :
Cho hình lăng trụ đứng MNPQ.M’N’P’Q’ có đáy MNPQ là hình thang vuông tại M và N. Kích thước các cạnh như Hình 10.11. Tính thể tích hình lăng trụ.
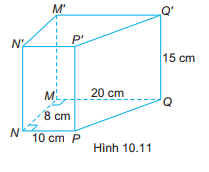
Bài 27 :
Một hình lăng trụ đứng được ghép bởi một hình lăng trụ đứng tam giác và một hình hộp chữ nhật có kích thước như trong Hình 10.12. Tính thể tích của hình lăng trụ ABCEF.A’B’C’E’F’.
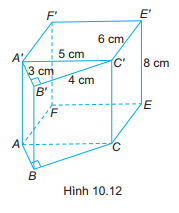
Bài 28 :
Một hình lăng trụ đứng, đáy là hình thang, chiều cao hình lăng trụ bằng 5 cm. Thể tích của hình lăng trụ nói trên bằng 50 cm3. Diện tích một đáy lăng trụ bằng:
A.10 cm2
B.250 cm2
C.55 cm2
D.10 cm3
Bài 29 :
Cho hình lăng trụ đứng tam giác, diện tích đáy bằng \(10c{m^2}\), chiều cao của hình lăng trụ là 5cm. Thể tích của hình lăng trụ đó là:
A. \(15c{m^2}\).
B. \(50c{m^2}\).
C. \(45c{m^3}\).
D. \(50c{m^3}\).
Bài 30 :
Cho hình lăng trụ đứng ABCD.A’B’C’D’ có đáy ABCD là hình chữ nhật, \(AB = 4cm,BC = 5cm\). Chiều cao của hình lăng trụ \(h = 2,5cm\). Diện tích xung quanh của hình lăng trụ ABCD.A’B’C’D’ là:
A. \(50c{m^2}\).
B. \(45c{m^2}\).
C. \(60c{m^2}\).
D. \(22,5c{m^2}\).




















Danh sách bình luận