Đề bài

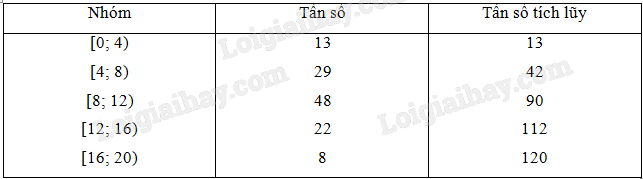
Hãy tính các số đặc trưng cho mẫu số liệu trong Bảng 3.1 và giải thích ý nghĩa của các giá trị thu được.

Phương pháp giải

Sử dụng công thức số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\bar x\)

                                              \(\bar x = \frac{{{m_1}{x_1} +  \ldots  + {m_k}{x_k}}}{n}\)

Trong đó \(n = {m_1} +  \ldots  + {m_k}\) là cỡ mẫu và  là giá trị đại diện của nhóm \(\left[ {{a_i},{a_{i + 1}}} \right)\)

Để tính trung vị của mẫu số liệu ghép nhóm, ta làm như sau:

Bước 1: Xác định nhóm chưa trung vị. Giả sử đó là nhóm thứ \(p:\left[ {{a_p};\;{a_{p + 1}}} \right)\).

Bước 2: Trung vị là \({M_e} = {a_p} + \frac{{\frac{n}{2} - \left( {{m_1} +  \ldots  + {m_{p - 1}}} \right)}}{{{m_p}}}.\;\left( {{a_{p - 1}} - {a_p}} \right),\)

Trong đó n là cỡ mẫu, \({m_p}\)là tần số nhóm p. Với \(p = 1\), ta quy ước \({m_1} +  \ldots  + {m_{p - 1}} = 0\)

Để tìm mốt của mẫu số liệu ghép nhóm, ta thực hiện theo các bước sau:

Bước 1: Xác định nhóm có tần sốớn nhất (gọi là nhóm chứa mốt), giả sử là nhóm \(j:\left[ {{a_j};\;{a_{j + 1}}} \right)\).

Bước 2: Mốt được xác định là: \({M_0} = {a_j} + \frac{{{m_j} - {m_{j - 1}}}}{{\left( {{m_j} - {m_{j - 1}}} \right) + \left( {{m_j} - {m_{j + 1}}} \right)}}.h\).

Trong đó \({m_j}\) là tần số của nhóm j (quy ước \({m_0} = {m_{k + 1}} = 0)\) và h là độ dài của nhóm.

Lời giải của GV Loigiaihay.com

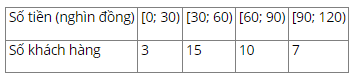
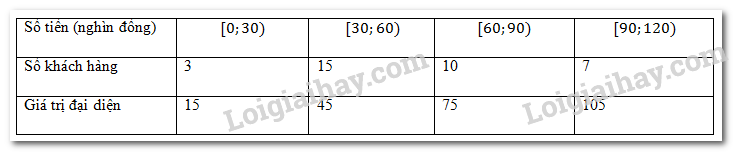
Ta có:

Số trung bình là \(\bar x = \frac{{3 \times 15 + 15 \times 45 + 10 \times 75 + 7 \times 105}}{{3 + 15 + 10 + 7}} = 63\)

Cỡ mẫu là: \(n = \;3\; + \;15\; + \;10\; + \;7\; = 35\)

Ý nghĩa: Xấp xỉ bằng số trung bình của mẫu số liệu gốc, cho biết vị trí trung tâm của mẫu số liệu và đại diện cho mẫu số liệu

Trung vị là \({x_{18}}\) thuộc nhóm \(\left[ {30;60} \right)\), do đó

\(p = 2,\;{a_2} = 30;\;{m_2} = 15;\;\;{m_1} = 3;\;\;{a_3} - {a_2} = 30\) và ta có:

\({M_e} = 30 + \frac{{\frac{{35}}{2} - 3}}{{15}} \times 30 = 59\).