Khảo sát thời gian tự học của các học sinh trong lớp theo mẫu bên.
a) Hãy lập bảng thống kê cho mẫu số liệu ghép nhóm thu được
b) Có thể tính chính xác thời gian tự học trung bình của các học sinh trong lớp không?
c) Có cách nào tính gần đúng thời gian tự học trung bình của các học sinh trong lớp dựa trên mẫu số liệu ghép nhóm này không?
Để chuyển mẫu số liệu không ghép nhóm sang mẫu số liệu ghép nhóm, ta làm như sau:
Bước 1: Chia miền giá trị của mẫu số liệu thành một số nhóm theo tiêu chí cho trước.
Bước 2: Đếm số giá trị của mẫu số liệu thuộc mỗi nhóm (tần số) và lập bảng thống kê cho mẫu số liệu ghép.
Dựa trên mẫu số liệu ghép nhóm, có thể ước lượng các số đặc trưng đo xu thế trung tâm cho mẫu số liệu gốc.
a)
b) Không thể tính chính xác, chúng ta chỉ có thể tinh số gần đúng thời gian tự học trung bình của các học sinh trong lớp
c) Giá trị đại diện của nhóm bằng trung bình giá trị đầu mút phải và trái của nhóm đó
Nhóm \( \ge 4.5\) là nhóm mở nên ta dựa theo nhóm gần đó nhất là nhóm [3;4.5) để lấy giá trị đại diện
Số trung binh của mẫu số liệu: : \(\bar x = \frac{{0.75 \times 8 + 2.25 \times 23 + 2.75 \times 6 + 5.25 \times 3}}{{40}} = 2.25\).

Các bài tập cùng chuyên đề
Bài 1 :
Tìm cân nặng trung bình của học sinh lớp 11D cho trong bảng 3.5:

-
A.
\(56,24\).
-
B.
\(54,33\).
-
C.
\(51,81\).
-
D.
\(53,83\)
Bài 2 :
Tổng lượng mưa trong tháng 8 đo được tại một trạm quan trắc đặt tại Vũng Tàu từ năm 2002 đến năm 2020 được ghi lại dưới đây (đơn vị: mm)
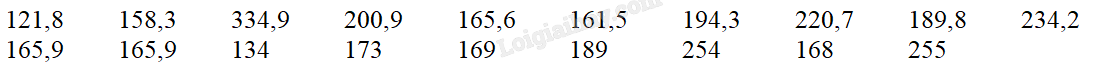
Số trung bình của bảng số liệu tần số ghép nhóm sau gần bằng giá trị nào sau đây?

-
A.
\(175\).
-
B.
\(180\).
-
C.
\(185\).
-
D.
\(188\).
Bài 3 :
Tìm hiểu thời gian xem ti vi trong tuần trước (đơn vị: giờ) của một số học sinh thu được kết quả sau:

Tính thời gian xem ti vi trung bình trong tuần trước của các bạn học sinh này.
Bài 4 :
Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:
|
Thời gian (phút) |
[0;20) |
[20; 40) |
[40; 60) |
[60; 80) |
[80; 100) |
|
Số học sinh |
5 |
9 |
12 |
10 |
6 |
Giá trị đại diện của nhóm \(\left[ {20;40} \right)\) là
A. 10
B. 20
C. 30
D. 40
Bài 5 :
Cơ cấu dân số Việt Nam năm 2020 theo độ tuổi được cho trong bảng sau:
(Theo: http://ourworldindata.org)
Chọn 80 là giá trị đại diện cho nhóm trên 65 tuổi. Tính tuổi trung bình của người Việt Nam năm 2020.
Bài 6 :
Hãy ước lượng cân nặng trung bình của học sinh trong Ví dụ 2 sau khi ghép nhóm và so sánh kết quả tìm được với cân nặng trung bình của mẫu số liệu gốc.
Bài 7 :
Hãy ước lượng trung bình số câu trả lời đúng của các học sinh lớp 11A1 trong Hoạt động 2.
Bài 8 :
Các bạn học sinh lớp 11A1 trả lời 40 câu hỏi trong một bài kiểm tra. Kết quả được thống kê ở bảng sau:

a) Tính giá trị đại diện \({c_i},1 \le i \le 5\), của từng nhóm số liệu.
b) Tính \({n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}\).
c) Tính \(\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}}}{{40}}\).
Bài 9 :
Người ta đếm số xe ô tô đi qua một trạm thu phí mỗi phút trong khoảng thời gian từ 9 giờ đến 9 giờ 30 phút sáng. Kết quả được ghi lại ở bảng sau:

a) Tính số xe trung bình đi qua trạm thu phí trong mỗi phút.
b) Tổng hợp lại số liệu trên vào bảng tần số ghép nhóm theo mẫu sau:

c) Hãy ước lượng trung bình số xe đi qua trạm thu phí trong mỗi phút từ bảng tần số ghép nhóm trên.
Bài 10 :
Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
A. \(\begin{array}{*{20}{c}}{\left[ {7;9} \right)}\end{array}\).
B. \(\begin{array}{*{20}{c}}{\left[ {9;11} \right)}\end{array}\).
C. \(\begin{array}{*{20}{c}}{\left[ {11;13} \right)}\end{array}\).
D. \(\begin{array}{*{20}{c}}{\left[ {13;15} \right)}\end{array}\).
Bài 11 :
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng).

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng sau đây?
-
A.
[7;9)
-
B.
[9;11)
-
C.
[11;13)
-
D.
[13;15)
Bài 12 :
Quãng đường (km) các cầu thủ (không tính thủ môn) chạy trong một trận đấu bóng đá tại giải ngoại hạng Anh được cho trong bảng thống sau:

Tính quãng đường trung bình một cầu thủ chạy trong trận đấu này.
Bài 13 :
Thống kê số lần đi học muộn trong học kì của các bạn trong lớp, Nam thu được kết quả sau:

Trung bình mỗi học sinh trong lớp đi muộn bao nhiêu buổi trong học kì?
Bài 14 :
Cho mẫu số liệu ghép nhóm về tuổi thọ (đơn vị tính là năm) của một loại bóng đèn mới như sau:

Số trung bình của mẫu số liệu là
A. \(5,0\)
B. \(5,32\)
C. \(5,57\)
D. \(6,5\)
Bài 15 :
Nồng độ cồn trong hơi thở (đơn vị tính là miligram/1 lít khí thở) của 20 lái xe ô tô vi phạm được cho như sau:
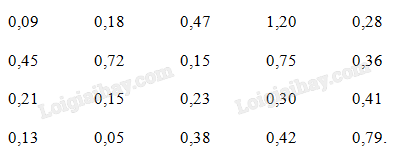
Theo quy định, mức phạt nồng độ cồn đối với lái xe ô tô như sau:
Mức 1. Nồng độ cồn trong hơi thở chưa vượt quá 0,25 phạt từ 6 đến 8 triệu đồng;
Mức 2. Nồng độ cồn trong hơi thở từ trên 0,25 đến 0,4 phạt từ 16 đến 18 triệu đồng;
Mức 3. Nồng độ cồn trong hơi thở vượt quá 0,4 phạt từ 30 đến 40 triệu đồng.
a) Lập bảng thống kê biểu diễn số lượng lái xe vi phạm theo mức tiền bị phạt.
b) Trung bình mỗi lái xe bị phạt bao nhiêu tiền? Tổng số tiền phạt của 20 lái xe khoảng bao nhiêu?
Bài 16 :
Một kĩ thuật viên ghi lại cân nặng của 20 chi tiết máy ở bảng sau (đơn vị: gam)

a) Tính cân nặng trung bình của mỗi chi tiết máy.
b) Lập bảng tần số ghép nhóm của mẫu số liệu trên với nhóm đầu tiên là \(\left[ {5,40;5,45} \right)\) và ước lượng số trung bình của mẫu số liệu ghép nhóm trên.
Bài 17 :
Tìm hiểu thời gian chạy cự li 1000 m (đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:

Thời gian (giây) chạy trung bình cự li 1000 m của các bạn học sinh là
-
A.
130,35
-
B.
131,03
-
C.
130,4
-
D.
132,5
Bài 18 :
Người ta tiến hành phỏng vấn 50 người về một mẫu áo phông mới. Người điều tra yêu cầu cho điểm mẫu áo đó theo thang điểm 100. Kết quả được trình bày trong bảng sau:
|
Nhóm |
[50;60) |
[60;70) |
[70;80) |
[80;90) |
[90;100) |
|
Số lượng |
9 |
10 |
23 |
6 |
2 |
Điểm trung bình của mẫu áo trong mẫu số liệu trên là
-
A.
$74,1$.
-
B.
$74,34$.
-
C.
$71,14$.
-
D.
$71,4$.
Bài 19 :
Xác định số trung bình cộng của mẫu số liệu ghép nhóm trong bài toán ở Luyện tập 2.
Bài 20 :
Xét mẫu số liệu trong Ví dụ 2 được cho dưới dạng bảng tần số ghép nhóm (Bảng 4).

a) Tìm trung điểm \({x_1}\) của nửa khoảng (tính bằng trung bình cộng của hai đầu mút) ứng với nhóm 1. Ta gọi trung điểm \({x_1}\) là giá trị đại diện của nhóm 1.
b) Bằng cách tương tự, hãy tìm giá trị đại diện của bốn nhóm còn lại. Từ đó, hãy hoàn thiện các số liệu trong Bảng 7.
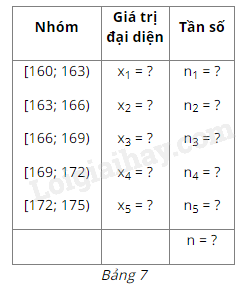
c) Tính giá trị \(\overline x \) cho bởi công thức sau:
\(\overline x = \frac{{{n_1}{x_1} + {n_2}{x_2} + ... + {n_5}{x_5}}}{n}\)
Bài 21 :
Một cửa hàng sách thống kê số truyện thiếu nhi bán được trong hai tháng ở bảng sau:

Hãy ước lượng số trung bình, mốt và các tứ phân vị của mẫu số liệu ghép nhóm trên.
Bài 22 :

Thời gian (giờ) sử dụng mạng xã hội trung bình trong ngày của nhóm học sinh là
A. 1,0.
B. 1,25.
C. 1,35.
D. 1,5.
Bài 23 :
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
-
A.
[7;9)
-
B.
[9;11)
-
C.
[11;13)
-
D.
[13;15)
Bài 24 :
Để chuẩn bị cho tiết học “Mạng xã hội: lợi và hại” (Hoạt động thực hành trải nghiệm môn Toán, lớp 10), giáo viên đã khảo sát thời gian sử dụng mạng xã hội trong một ngày của học sinh trong lớp 10A1 mình dạy và thu được mẫu số liệu như sau:

Thời gian trung bình (phút) sử dụng mạng xã hội của học sinh lớp 10A1 xấp xỉ bằng
-
A.
35
-
B.
30,5
-
C.
36,3
-
D.
33,6
Bài 25 :
Bác Hùng thống kê lại đường kính thân gỗ của một số cây Keo tai tượng 5 năm tuổi được trồng ở
một lâm trường ở bảng sau:

Hãy tìm số trung bình cộng của mẫu số liệu ghép nhóm trên.
-
A.
36,9 cm
-
B.
33,9 cm
-
C.
35,9 cm
-
D.
34,9 cm
Bài 26 :
Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được ghi lại ở bảng sau:

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?
-
A.
[7;9)
-
B.
[9;11)
-
C.
[11;13)
-
D.
[13;15)
Bài 27 :
Điểm thi môn Toán trong Kỳ thi Tốt nghiệp trung học phổ thông của 690 học sinh trường THPT X được thống kê bởi bảng số liệu như sau:

Điểm trung bình môn Toán của mẫu số liệu trên xấp xỉ bằng
-
A.
5,4
-
B.
6,4
-
C.
7,4
-
D.
7,0
Bài 28 :
Cân nặng (kg) của 50 quả mít trong đợt thu hoạch của một trang trại được thống kê trong bảng dưới đây:

Khối lượng trung bình của 50 quả mít trên bằng
-
A.
8,72 kg
-
B.
9,12 kg
-
C.
8,82 kg
-
D.
8,52 kg
Bài 29 :
Thời gian (phút) đi từ nhà đến trường của bạn An trong 35 ngày liên tiếp được cho trong bảng sau:

Thời gian trung bình bạn An dành ra để đi từ nhà đến trường trong 35 ngày đó là (kết quả làm tròn đến hàng phần mười)
-
A.
24,8 phút.
-
B.
25,8 phút.
-
C.
25,4 phút.
-
D.
24,2 phút.
Bài 30 :
Số câu trả lời đúng một bài thi trắc nghiệm môn Toán gồm 50 câu của lớp 11A ở một trường THPT như sau:

Số trung bình câu đúng của mẫu số liệu trên (làm tròn kết quả đến hàng đơn vị) là
-
A.
30.
-
B.
33.
-
C.
32.
-
D.
31.






















Danh sách bình luận