Đề bài

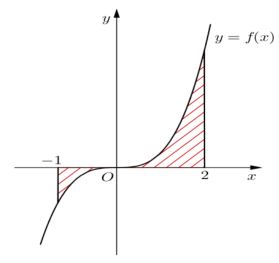
Gọi \(S\) là diện tích hình phẳng \(\left( H \right)\) giới hạn bởi các đường $y=f\left( x \right),~$trục hoành và hai đường thẳng \(x =  - 1,x = 2\) (như hình vẽ). Đặt $a=\underset{-1}{\overset{0}{\mathop \int }}\,f\left( x \right)dx,~b=\underset{0}{\overset{2}{\mathop \int }}\,f\left( x \right)dx.$  Mệnh đề nào sau đây đúng?

• A. \(S = b - a.\)    
• B. \(S = b + a.\)
• C. \(S =  - b + a.\)            
• D. \(S =  - b - a.\)

Phương pháp giải

- Công thức tính diện tích hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục \(Ox\) và hai đường thẳng \(x = a,x = b\left( {a < b} \right)\) là:\(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \)

- Công thức tổng 2 tích phân  $\int\limits_a^b {f(x)dx}  + \int\limits_b^c {f(x)dx}  = \int\limits_a^c {f(x)dx} $

Lời giải của GV Loigiaihay.com

Diện tích hình phẳng là S =\(\int\limits_{ - 1}^2 {\left| {f(x)} \right|} dx\)

Dựa vào hình vẽ ta có được: $S = \int\limits_{ - 1}^0 {(0 - f(x))dx}  + \int\limits_0^2 {f(x)dx}  =  - \int\limits_{ - 1}^0 {f(x)dx + } \int\limits_0^2 {f(x)dx}  = b - a$

Đáp án : A

Chú ý

Một số em không để ý tới dấu của \(f\left( x \right)\) trên từng khoảng nên sẽ có cách làm sai như sau:

$S = \int\limits_{ - 1}^0 {f\left( x \right)dx}  + \int\limits_0^2 {f\left( x \right)dx}  = a + b$ và chọn đáp án B là sai.