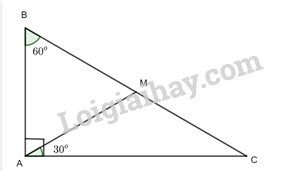
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
a) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ suy ra góc A bằng góc C.
b) Chứng minh tam giác ABM cân có 1 góc bằng 60 độ
c) Dùng tính chất tổng 3 góc trong 1 tam giác bằng 180 độ để tính số đo 3 góc từ đó suy ra tam giác đều
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ {90^o} + {60^o} + \widehat C = {180^o}\\ \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
Suy ra tam giác CAM cân tại M.
b) Xét tam giác CAM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ \widehat {CMA} = {120^o}\\ \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Suy ra MB = MC. Mà M nằm giữa B và C
Do đó M là trung điểm của BC.

Các bài tập cùng chuyên đề
Bài 1 :
Cho tam giác ABC vuông cân ở A. Trên đáy BC lấy hai điểm M, N sao cho BM = CN = AB. Tính \(\widehat {MAN}\).
-
A.
30\(^\circ \)
-
B.
45\(^\circ \)
-
C.
67,5\(^\circ \)
-
D.
60\(^\circ \)
Bài 2 :
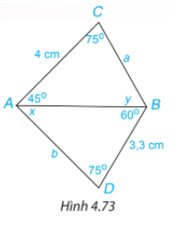
Cho Hình 4.73. Hãy tìm số đo x, y của các góc và độ dài a, b của các đoạn thẳng trên hình vẽ.
Bài 3 :
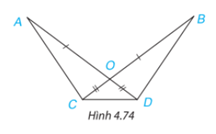
Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:
a) AC = BD;
b) \(\Delta \)ACD = \(\Delta \)BDC.
Bài 4 :
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của đoạn thẳng AB sao cho AM = AN. Chứng minh rằng MB = NB và góc AMB bằng góc ANB.
Bài 5 :
Cho tam giác ABC cân tại A có \(\widehat {A{\rm{ }}} = 120^\circ \). Trên cạnh BC lấy hai điểm M, N sao cho MA, NA lần lượt vuông góc với AB, AC. Chứng minh rằng:
a) \(\Delta \)BAM = \(\Delta \)CAN;
b) Các tam giác ANB, AMC lần lượt cân tại N, M.
Bài 6 :
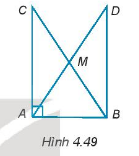
Cho tam giác ABC vuông tại đỉnh A. Gọi M là trung điểm của BC và D là điểm nằm trên tia đối của tia MA sao cho MD = MA (H.4.49). Chứng minh rằng:
a) \(\Delta ABD\) vuông tại B.
b) \(\Delta ABD = \Delta BAC\)
c) Các tam giác AMB, AMC là các tam giác cân tại đỉnh M.
Bài 7 :
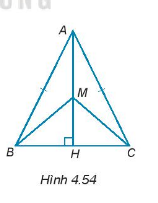
Cho tam giác ABC cân tại đỉnh A có đường cao AH. Cho M là một điểm tuỳ ý trên đường thẳng AH sao cho M không trùng với A(H.4.54). Chứng minh rằng: \(\widehat {MBA} = \widehat {MCA}\).
Bài 8 :
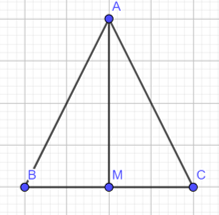
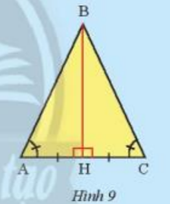
Cho tam giác ABC cân tại A (Hình 5). Gọi M là trung điểm cạnh BC. Nối A với M. Em hãy làm theo gợi ý sau để chứng minh \(\widehat {ABC}\)=\(\widehat {ACB}\).
Xét \(\Delta AMB\) và \(\Delta AMC\) có:
AB = ? (?)
MB = MC (?)
AM là cạnh ?
Vậy \(\Delta AMB\) =\(\Delta AMC\) (c.c.c)
Suy ra \(\widehat {ABC}\)=\(\widehat {ACB}\)
Bài 9 :
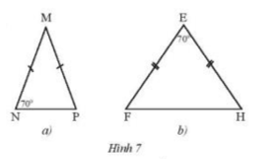
Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.
Bài 10 :
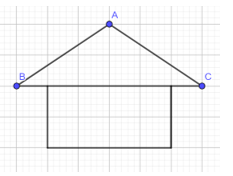
Trong hình mái nhà ở Hình 8, tính góc B và góc C, biết \(\widehat A\)= \({110^o}\).
Bài 11 :
Cho tam giác ABC có \(\widehat A\)=\(\widehat C\). Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại điểm H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.
Xét \(\Delta AHB\)và \(\Delta CHB\)cùng vuông tại H, ta có:
BH là cạnh góc vuông ?
\(\widehat {HAB}\) = \(\widehat {HCB}\) suy ra \(\widehat {ABH} = \widehat {CBH}\) (?)
Vậy \(\Delta AHB = \Delta CHB\). Suy ra BA = BC
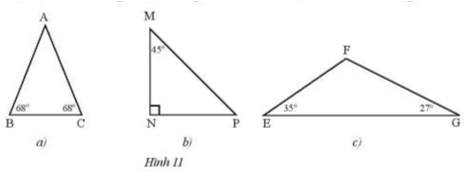
Bài 12 :
Tìm các tam giác cân trong Hình 11 và đánh dấu vào các cạnh bằng nhau.
Bài 13 :
Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.
a) Chứng minh rẳng \(\widehat {ABF} = \widehat {ACE}\)
b) Chứng minh rằng tam giác AEF cân
c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân
Bài 14 :
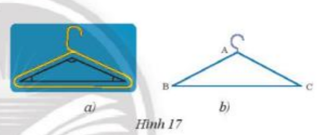
Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và \(\widehat B\)= 35°. Tìm số đo các góc còn lại và chu vi của tam giác ABC.
Bài 15 :
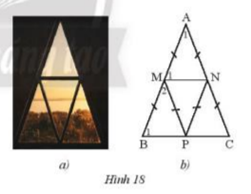
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.
a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).
b) Chứng minh MN // BC, MP // AC.
c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
Bài 16 :
Cho tam giác ABC vuông tại A (AB < AC), vẽ đường cao AH. Trên tia đối của HC lấy điểm D sao cho HD = HC.
a) Chứng minh rằng AD = AC.
b) Chứng minh rằng \(\widehat {ADH} = \widehat {BAH}\)
Bài 17 :
Cho tam giác ABC vuông tại A (AB < AC). Trên cạnh BC lấy điểm N sao cho BA = BN. Kẻ \(BE \bot AN\)(E ∈ AN).
a) Chứng minh rằng BE là tia phân giác của giác ABN.
b) Kẻ đường cao AH của tam giác ABC. Gọi K là giao điểm của BH với CE. Chứng minh rằng NK // CA.
c) Đường thẳng BK cắt AC tại F. Gọi G là giao điểm của đường thẳng AB với NF. Chứng minh rằng tam giác GBC cân.
Bài 18 :
Cho tam giác ABC cân tại A. Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC, cắt cạnh AC tại N. Chứng minh tam giác AMN cân.
Bài 19 :
Cho tam giác ABC cân tại A có M là trung điểm cạnh AC và N là trung điểm cạnh AB. Chứng minh \(BM = CN\)
Bài 20 :
Cho tam giác ABC có \(\widehat A = 120^\circ \). Tia phân giác của góc A cắt cạnh BC tại D. Đường thẳng qua D song song với AB cắt cạnh AC tại E. Chứng minh rằng tam giác ADE đều.
Bài 21 :
Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của cạnh huyền BC. Chứng minh tam giác MAB vuông cân.
Bài 22 :
Trong thiết kế của một ngôi nhà, độ nghiêng của mái nhà so với phương nằm ngang phải phù hợp với kết cấu của ngôi nhà và vật liệu làm mái nhà. Hình 77 mô tả mặt cắt đứng của ngôi nhà, trong đó độ nghiêng của mái nhà so với phương nằm ngang được biểu diễn bởi số đo góc ở đáy của tam giác ABC cân tại A.
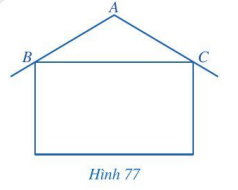
Tính độ nghiêng của mái nhà so với mặt phẳng nằm ngang trong mỗi trường hợp sau:
a) Góc ở đỉnh A là (khoảng) 120° đối với mái nhà lợp bằng ngói;
b) Góc ở đỉnh A là (khoảng) 140° đối với mái nhà lợp bằng fibro xi măng;
c) Góc ở đỉnh A là (khoảng) 148° đối với mái nhà lợp bằng tôn.
Bài 23 :
Trong hình 6, tính góc B và góc C biết \(\widehat {{A^{}}} = {138^o}\)

Bài 24 :
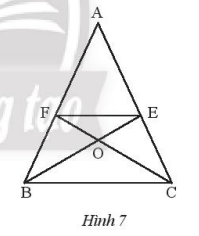
Cho hình 7, biết AB = AC và BE là tia phân giác của \(\widehat {ABC}\), CF là tia phân giác của góc \(\widehat {ACB}\). Chứng minh rằng:
a) \(\Delta ABE = \Delta ACF\)
b) Tam giác OEF cân
Bài 25 :
Cho tam giác MEF cân tại M, có \(\widehat M = {80^o}\)
a) Tính \(\widehat E{,^{}}\widehat F\)
b) Gọi N, P lần lượt là trung điểm của ME, MF. Chứng minh rằng tam giác MNP cân.
c) Chứng minh rằng NP // EF
Bài 26 :
Ở Hình 36 có AB song song cới CD, BC song song với AD. Tia phân giác của góc BAD cắt BC tại E và cắt tia DC tại F.
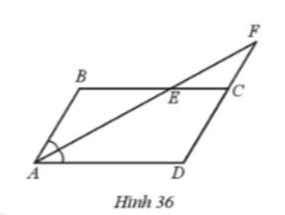
a) Chứng minh các tam giác ABE, CEF, DAF là các tam giác cân.
b) Tính số đo mỗi góc của tam giác ADF, biết \(\widehat {BAD} = 60^\circ \)
Bài 27 :
Cho tam giác ABC. Gọi I là trung điểm của BC. Tính số đo góc BAC, biết IA = IB = IC.
Bài 28 :
a)Chứng minh rằng nếu tam giác ABC có đường trung tuyến xuất phát từ A bằng một nửa cạnh BC thì tam giác đó vuông tại đỉnh A.
b)Cho đoạn thẳng AB. Hãy nêu một cách sử dụng kết quả của câu a để vẽ đường thẳng vuông góc với AB tại A (bằng thước và compa)
Bài 29 :
Tính chất nào sau đây không phải của tam giác \(ABC\) cân tại \(C\):A. Trung tuyến \(AM\)và \(BN\)của tam giác \(ABC\) bằng nhau.
B. \(\angle A < {90^o}\).
C. \(AC > AB\).
D. \(\angle A = \angle B\)
Bài 30 :
Nếu tam giác \(ABC\) cân tại B thìA. Đường trung tuyến AM đồng thời là đường phân giác
B. Đường trung tuyến CP đồng thời là đường trung trực
C. Đường trung tuyến BN đồng thời là đường phân giác
D. Đường trung tuyến AM đồng thời là đường trung trực


















Danh sách bình luận