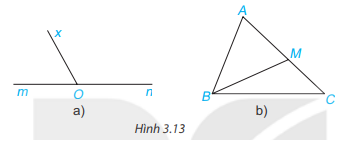
Cho Hình 3.13, hãy kể tên các cặp góc kề bù.
2 góc có một cạnh chung, hai cạnh còn lại là hai tia đối nhau được gọi là 2 góc kề bù.
a) Góc xOm và xOn là 2 góc kề bù vì 2 góc này có chung cạnh Ox, cạnh Om là tia đối của On.
b) Góc AMB và CMB là 2 góc kề bù vì 2 góc này có chung cạnh MB, cạnh MA là tia đối của MC.

Các bài tập cùng chuyên đề
Bài 1 :
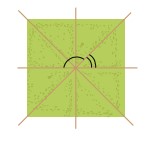
Quan sát hình vẽ bên. Em hãy nhận xét về mối quan hệ về đỉnh, về cạnh của hai góc được đánh dấu.
Bài 2 :
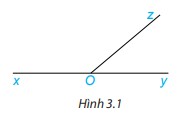
Cho ba tia Ox, Oy, Oz như Hình 3.1, trong đó Ox và Oy là hai tia đối nhau.
a) Em hãy nhận xét về quan hệ về đỉnh, về cạnh của hai góc xOz và zOy.
b) Đo rồi tính tổng số đo góc hai góc xOz và zOy.
Bài 3 :
Hai góc được đánh dấu trong hình nào dưới đây là hai góc kề bù?
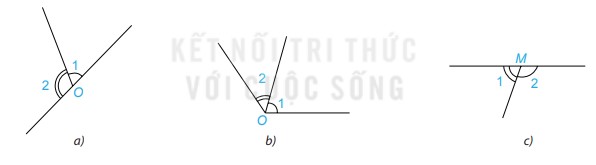
Bài 4 :
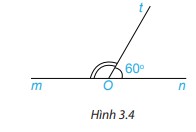
Viết tên hai góc kề bù trong Hình 3.4 và tính số đo góc mOt
Bài 5 :
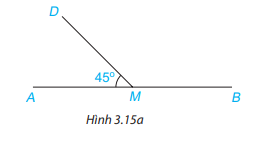
Cho Hình 3.15a, biết \(\widehat {DMA} = 45^\circ \). Tính số đo góc DMB
Bài 6 :
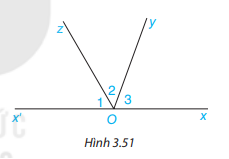
Cho Hình 3.51, trong đó Ox và Ox’ là hai tia đối nhau
a) Tính tổng số đo ba góc O1, O2, O3 .
Gợi ý: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\), trong đó \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat {x'Oy}\)
b) Cho \(\widehat {{O_1}} = 60^\circ ,\widehat {{O_3}} = 70^\circ \). Tính \(\widehat {{O_2}}\)
Bài 7 :
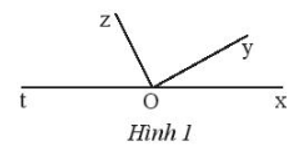
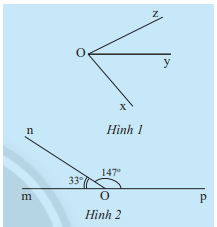
a) Quan sát Hình 1 và cho biết hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có:
- Cạnh nào chung?
- Điểm trong nào chung?
b) Hãy đo các góc \(\widehat {xOy},\widehat {yOz},\widehat {xOz}\) trong Hình 1 rồi so sánh tổng số đo của \(\widehat {xOy}\) và \(\widehat {yOz}\) với \(\widehat {xOz}\).
c) Tính tổng số đo của hai góc \(\widehat {mOn}\) và \(\widehat {nOp}\) trong Hình 2.
Bài 8 :
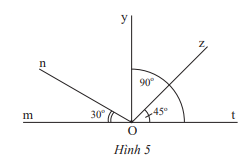
Quan sát hình 5.
a) Tìm các góc kề với \(\widehat {tOz}\)
b) Tìm số đo của góc kề bù với \(\widehat {mOn}\).
c) Tìm số đo của \(\widehat {nOy}\)
d) Tìm số đo của góc kề bù với \(\widehat {tOz}\).
Bài 9 :
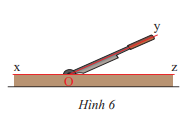
Hình 6 mô tả con dao và bàn cắt. Hãy tìm hai góc kề bù có trong hình
Bài 10 :
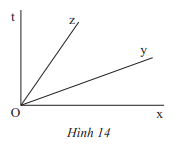
Quan sát Hình 14.
a) Tìm các góc kề với \(\widehat {xOy}\).
b) Tìm số đo của \(\widehat {tOz}\) nếu cho biết \(\widehat {xOy} = 20^\circ ;\widehat {xOt} = 90^\circ ;\widehat {yOz} = \widehat {tOz}\).
Bài 11 :
Cho hai góc \(\widehat {xOy},\widehat {yOz}\) kề bù với nhau. Biết \(\widehat {xOy} = 25^\circ \). Tính \(\widehat {yOz}\).
Bài 12 :
Cho hai góc kề nhau \(\widehat {AOB}\) và \(\widehat {BOC}\) với \(\widehat {AOC} = 80^\circ \). Biết \(\widehat {AOB} = \frac{1}{5}.\widehat {AOC}\). Tính số đo các góc \(\widehat {AOB}\) và \(\widehat {BOC}\)
Bài 13 :
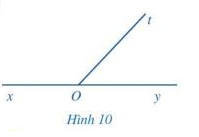
Quan sát hai góc xOt và yOt ở Hình 10, trong đó Ox và Oy là hai tia đối nhau.
a) Hai góc xOt và yOt có kề nhau không?
b) Tính \(\widehat {xOt} + \widehat {yOt}\)
Bài 14 :
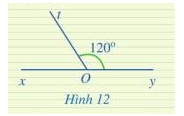
Tính góc xOt trong Hình 12
Bài 15 :
Hình 23 là một mẫu cửa có vòm tròn của một ngôi nhà. Nếu coi mỗi thanh chắn vòm cửa đó như một cạnh của góc thì các thanh chắn đó tạo ra các góc kề nhau. Theo em, mỗi góc tạo bởi hai thanh chắn vòm cửa đó khoảng bao nhiêu độ?
Bài 16 :
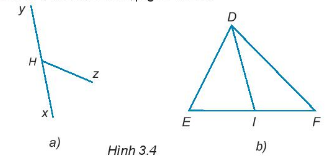
Cho hình 3.4, kể tên các cặp góc kề bù.
Bài 17 :
Vẽ góc \(\widehat {xAy} = {40^0}\). Vẽ \(\widehat {yAz}\) là góc kề bù với \(\widehat {xAy}\).
Bài 18 :
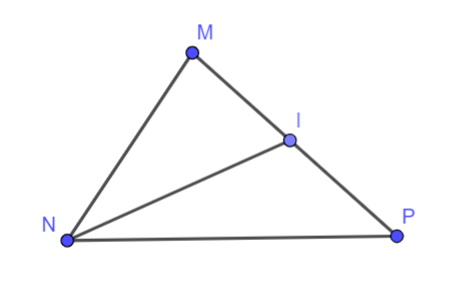
Quan sát hình vẽ bên. Góc kề bù với \(\widehat {MIN}\) là
A. \(\widehat {NMI}\)
B. \(\widehat {MNI}\)
C. \(\widehat {NIP}\)
D. \(\widehat {IPN}\)
Bài 19 :
Cho hình 3.1, hãy kể tên các cặp góc kề bù.
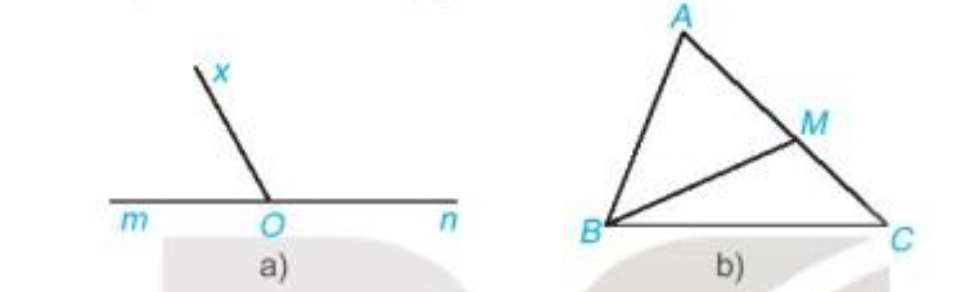
Bài 20 :
Cho hình 3.3 biết \(\widehat {DMA} = {45^o}\). Tính số đo góc DMB.
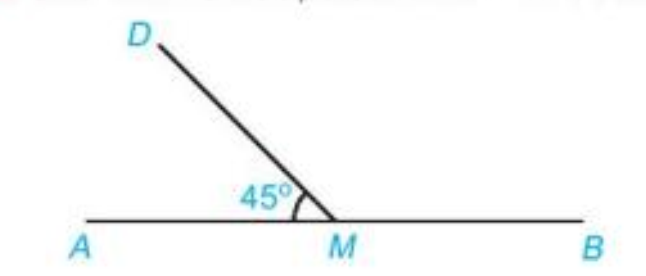
Bài 21 :
Cho hai đường thẳng \(xx'\) và \(yy'\) cắt nhau tại \(O\) sao cho \(\angle xOy = \dfrac{2}{3}\angle xOy'\). Tính số đo \(\angle xOy'\)?A. \({36^0}\)
B. \({72^0}\)
C. \({108^0}\)
D. \({18^0}\)
Bài 22 :
Cho góc vuông uOv và tia Oy đi qua một điểm trong của góc đó. Vẽ tia Ox sao cho Ou là tia phân giác của góc xOy. Vẽ tia Oz sao cho Ov là tia phân giác của góc yOz. Chứng minh rằng hai góc xOy và yOz là hai góc kề bù.
Bài 23 :
Cho hình 3.20, trong đó Ox và Ox’ là hai tia đối nhau.
a) Tính tổng số đo ba góc \({O_1},{O_2},{O_3}\).
b) Cho \(\widehat {{O_1}} = {60^o},\widehat {{O_3}} = {70^o}\). Tính \(\widehat {{O_2}}\)
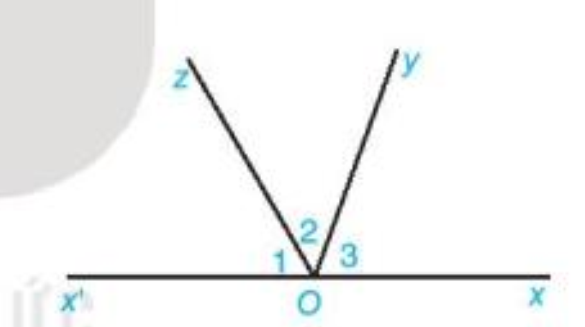
Bài 24 :
Cho hình 3.21 biết \(\widehat {xOy} = {120^o},\widehat {yOz} = {110^o}\). Tính số đo góc zOx.
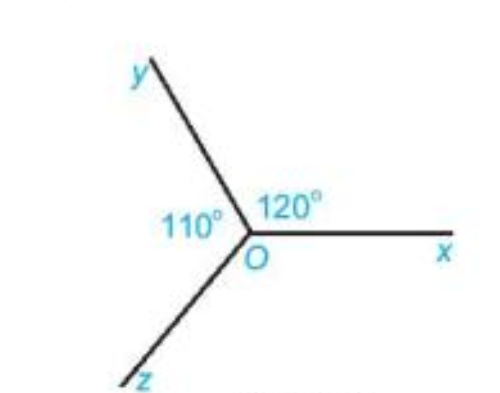
Bài 25 :
Tìm giá trị của x trong Hình 14
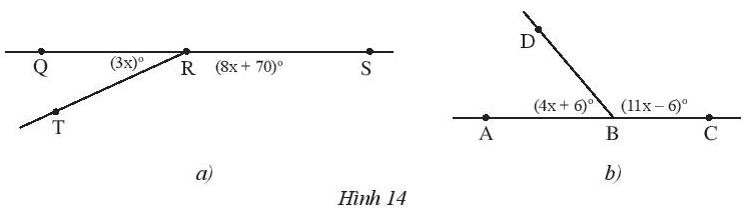
Bài 26 :
a) Đo các góc trong Hình 1.
b) Nêu tên các cặp góc kề bù.
Bài 27 :
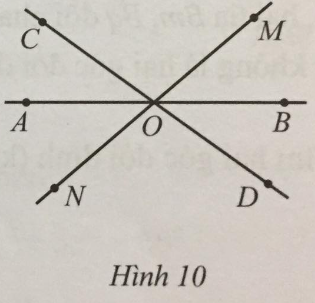
Quan sát Hình 10 và chỉ ra:
a) Bốn góc kề với góc AOC (không kể góc bẹt);
b) Hai góc kề bù với góc AOC.
Bài 28 :
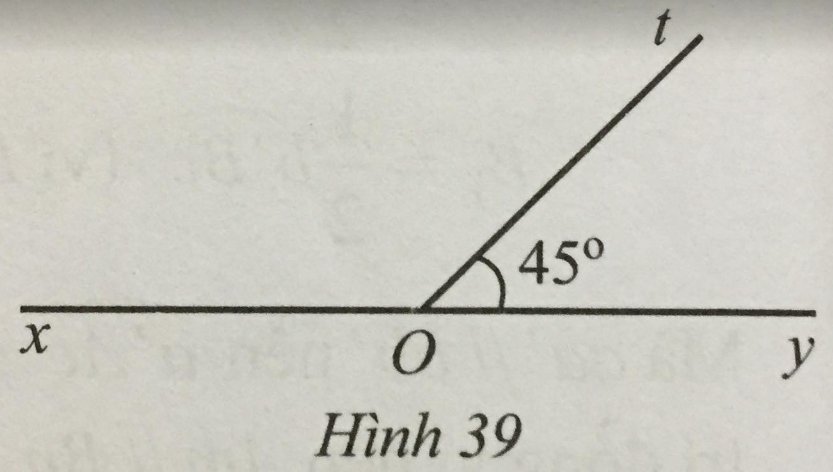
Số đo của góc xOt trong Hình 39 là:
A. 45°.
B. 135°.
C. 55°.
D. 90°.
Bài 29 :
Cho hình vẽ sau:
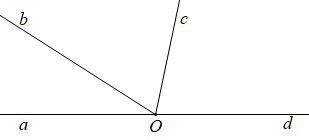
Số cặp góc kề bù (không kể góc không và góc bẹt) có trong hình vẽ trên là
-
A.
1;
-
B.
2;
-
C.
3;
-
D.
4.
Bài 30 :
Cho hình vẽ
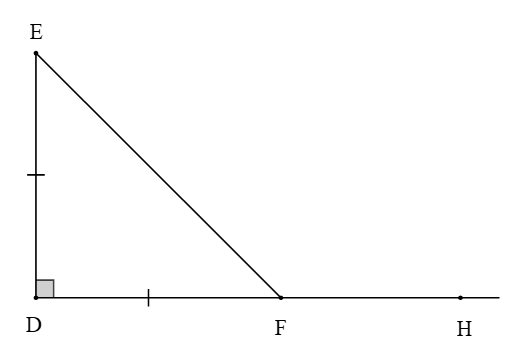
Số đo của \(\widehat {EFH}\) là
-
A.
\(105^\circ ;\)
-
B.
\(115^\circ ;\)
-
C.
\(125^\circ ;\)
-
D.
\(135^\circ .\)



















Danh sách bình luận