Vẽ đường thẳng $mn.$ Lấy điểm $O$ trên đường thẳng $mn,$ trên tia $Om$ lấy điểm $A,$ trên tia $On$ lấy điểm $B.$
Có bao nhiêu cặp tia trùng nhau gốc \(O?\)
-
A.
\(2\)
-
B.
\(4\)
-
C.
\(3\)
-
D.
\(0\)
Đáp án : A
Hai tia trùng nhau có cùng gốc và có một điểm chung khác gốc

Các cặp tia trùng nhau gốc \(O\) là:
\(OA,Om\) và \(OB,On\)
Vậy có hai cặp tia trùng nhau gốc \(O\)
Các bài tập cùng chuyên đề
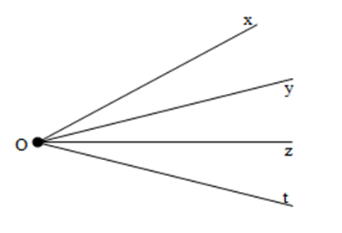
Kể tên các tia trong hình vẽ sau
Cho $AB$ và $Ax$ là hai tia trùng nhau. Hãy chọn hình vẽ đúng.
Cho tia $AB,$ lấy $M$ thuộc tia $AB.$ Khẳng định nào sau đây đúng?
Cho hai tia đối nhau $MA$ và $MB,$ $X$ là $1$ điểm thuộc tia $MA.$ Trong $3$ điểm $X,{\rm{ }}M,{\rm{ }}B$ điểm nào nằm giữa hai điểm còn lại?
Trong hình vẽ sau, có bao nhiêu tia
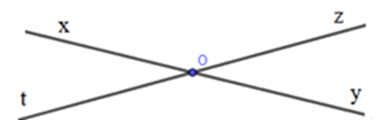
Vẽ hình theo cách diễn đạt sau:
+ Vẽ hai tia phân biệt $Ox$ và \(Oy\) chung gốc nhưng không đối nhau, không trùng nhau
+ Vẽ đường thẳng \(aa'\) cắt hai tia \(Ox;\,Oy\) theo thứ tự tại \(A\) và \(B\)(khác \(O\))
+ Vẽ điểm \(C\) nằm giữa hai điểm \(A;B\) sau đó vẽ tia \(Oz\) đi qua \(C\)
Có bao nhiêu tia phân biệt trên hình vẽ thu được.

















