Cho tam giác ABC có D là trung điểm cạnh AC. Biết \(AD = BD = CD = 5cm\) và \(BC = 6cm,\) tính độ dài cạnh AB.

Tam giác ABC có BD là đường trung tuyến bằng \(\frac{1}{2}AC\) nên tam giác ABC vuông tại B.
Kết hợp sử dụng định lí Pythagore.
Xét tam giác ABC có BD là đường trung tuyến bằng \(\frac{1}{2}AC\) nên tam giác ABC vuông tại B.
Có \(A{B^2} + B{C^2} = A{C^2}\) (đinh lí Pythagore)
\( \Rightarrow AB = \sqrt {A{C^2} - B{C^2}} = \sqrt {{{\left( {5 + 5} \right)}^2} - {6^2}} = 8\left( {cm} \right)\)

Các bài tập cùng chuyên đề
Bài 1 :
Cho góc nhọn \(xOy.\) Điểm H nằm trên tia phân giác của góc \(xOy.\) Hạ \(HA \,\bot \,{\rm{Ox,}}\,{\rm{HB}} \,\bot \,{\rm{Oy}}\) \(\left( {A \in {\rm{Ox}},\,B \in Oy} \right)\). Gọi D là hình chiếu của điểm A trên Oy, C là giao điểm của AD với OH.
Bài 2 :
Cho Hình 14. Tìm \(x\).
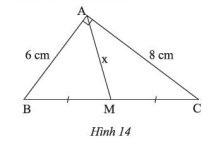
Bài 3 :
Cho tam giác \(ABC\) vuông tại \(A\), đường trung tuyến \(AM\). Biết \(AB = 8\)cm; \(AC = 15\)cm. Độ dài đoạn \(AM\) là:
A. 8,5cm
B. 8cm
C. 7cm
D. 7,5cm
Bài 4 :
Cho hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O. Gọi M, N lần lượt là hình chiếu của O trên AB, BC. Chứng minh: \(MN = \dfrac{1}{2}AC\)
Bài 5 :
1. Sử dụng tính chất tổng các góc của một tam giác bằng \({180^0}\) để chứng minh:
a) Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.
b) Tam giác ABC có đường trung tuyến AM bằng nửa BC thì tam giác vuông tại A.
2. Sử dụng tính chất hai đường chéo của hình chữ nhật bằng nhau để chứng minh a), b) của ý 1.


















Danh sách bình luận