a) Cho phân thức \(\frac{{2x}}{7}\). Hãy nhân cả tử và mẫu của phân thức này với \(3{x^2}\) rồi so sánh phân thức vừa nhận được với phân thức đã cho.
b) Cho phân thức \(\frac{{15{x^3}{y^2}}}{{25{x^2}{y^3}}}\). Hãy chia cả tử và mẫu của phân thức này cho \(5{x^2}{y^2}\) rồi so sánh phân thức vừa nhận được với phân thức đã cho.
Sử dụng phương pháp tính phép nhân đơn thức để thực hiện nhân cả tử và mẫu của phân thức này với \(3{x^2}\), sau đó so sánh phân thức vừa nhận được với phân thức đã cho.
Sử dụng phương pháp tính phép chia đơn thức để thực hiện chia cả tử và mẫu của phân thức này với \(5{x^2}{y^2}\), sau đó so sánh phân thức vừa nhận được với phân thức đã cho.
a) Ta có:
\(2x.3{x^2} = 6{x^3}\)
\(7.3{x^2} = 21{x^2}\)
Vậy phân thức nhận được là: \(\frac{{6{x^3}}}{{21{x^2}}}\)
Ta thấy phân thức vừa nhận được bằng với phân thức đã cho.
b) Ta có:
\(15{x^3}{y^2}:5{x^2}{y^2} = 3x\)
\(25{x^2}{y^3}:5{x^2}{y^2} = 5y\)
Vậy phân thức nhận được là: \(\frac{{3x}}{{5y}}\)
Ta thấy phân thức vừa nhận được bằng với phân thức đã cho.

Các bài tập cùng chuyên đề
Bài 1 :
Xét hai phân thức \(M = \dfrac{x}{y}\) và \(N = \dfrac{{{x^2} + x}}{{xy + y}}\)
a) Tính giá trị của các phân thức trên khi \(x = 3\), \(y = 2\) và khi \(x = - 1\), \(y = 5\).
Nêu nhận xét về giá trị của \(M\) và \(N\) khi cho \(x\) và \(y\) nhận những giá trị nào đó (\(y \ne 0\) và \(xy - y \ne 0\)).
b) Nhân tử thức của phân thức này với mẫu thức của phân thức kia, rồi so sánh hai đa thức nhận được.
Bài 2 :
Mỗi cặp phân thức sau đây có bằng nhau không? Tại sao?
a) \(\dfrac{{x{y^2}}}{{xy + y}}\) và \(\dfrac{{xy}}{{x + 1}}\)
b) \(\dfrac{{xy - y}}{x}\) và \(\dfrac{{xy - x}}{y}\)
Bài 3 :
a) Tính số thích hợp vào ?: 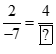
b) Hãy nhắc lại tính chất cơ bản của phân số.
Bài 4 :
Dùng tính chất cơ bản của phân thức, hãy giải thích vì sao có thể viết: \(\dfrac{{3{\rm{x}} + y}}{y} = \dfrac{{3{\rm{x}}y + {y^2}}}{{{y^2}}}\)
Bài 5 :
Tìm một đa thức thích hợp cho ô ? để có hai phân thức bằng nhau: \(\frac{{5x - 1}}{{6x - 7}} = \frac{?}{{6{x^2} - 7x}}\).
Bài 6 :
Dùng tính chất cơ bản của phân thức, hãy chứng minh:
a) \(\frac{{4 - x}}{{ - 2x}} = \frac{{x - 4}}{{2x}}\)
b) \(\frac{{{x^4}{y^3}{z^2}}}{{{x^2}{y^3}{z^4}}} = \frac{{{x^2}}}{{{z^2}}}\)
c) \(\frac{{y - x}}{{3 - x}} = \frac{{x - y}}{{x - 3}}\)
d) \(\frac{{x + y}}{x} = \frac{{{x^2} - {y^2}}}{{x\left( {x - y} \right)}}\)
Bài 7 :
Liệu phân thức nào đơn giản nhưng bằng phân thức \(\frac{{x - y}}{{{x^3} - {y^3}}}\) không nhỉ?
Bài 8 :
Nếu nhân cả tử và mẫu của phân thức \(\frac{{x + y}}{{x - y}}\) với 2x ta được phân thức mới nào? Giải thích vì sao phân thức mới nhận được bằng phân thức đã cho.
Bài 9 :
Khẳng định sau đúng hay sai? Vì sao?
\(\frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} = \frac{{2y}}{{3\left( {x - y} \right)}}\)
Bài 10 :
Giải thích vì sao \(\frac{{ - x}}{{1 - x}} = \frac{x}{{x - 1}}\)
Bài 11 :
Liệu phân thức nào đơn giản nhưng bằng phân thức \(\frac{{x - y}}{{{x^3} - {y^3}}}\) không nhỉ?
Bài 12 :
Dùng tính chất cơ bản của phân thức, giải thích vì sao các kết luận sau đúng.
\(a)\frac{{{{\left( {x - 2} \right)}^3}}}{{{x^2} - 2}} = \frac{{{{\left( {x - 2} \right)}^2}}}{2}\)
\(b)\frac{{1 - x}}{{ - 5{\rm{x}} - 1}} = \frac{{x - 1}}{{5{\rm{x}} - 1}}\)
Bài 13 :
Tìm đa thức thích hợp thay cho dấu: “?”: \[\frac{{y - x}}{{4 - x}} = \frac{?}{{x - 4}}\]
Bài 14 :
Tìm a sao cho hai phân thức sau bằng nhau:
\(\frac{{5{\rm{x}}}}{{x + 1}}\) và \(\frac{{ax\left( {x - 1} \right)}}{{\left( {1 - x} \right)\left( {x + 1} \right)}}\)
Bài 15 :
Phân thức \(\frac{{1 - x}}{{y - x}}\) bằng với phân thức nào sau đây?
-
A.
\(\frac{{x - 1}}{{y - x}}\)
-
B.
\(\frac{{1 - x}}{{x - y}}\)
-
C.
\(\frac{{x - 1}}{{x - y}}\)
-
D.
\(\frac{{y - x}}{{1 - x}}\)
Bài 16 :
Chọn cách viết đúng.
-
A.
\(\frac{A}{B} = \frac{{ - A}}{{ - B}}\)
-
B.
\(\frac{A}{B} = \frac{{ - A}}{{B}}\)
-
C.
\(\frac{A}{B} = \frac{{A}}{{ - B}}\)
-
D.
\(\frac{A}{B} = - \frac{{A}}{{B}}\)
Bài 17 :
Đâu là tính chất đúng của phân thức đại số?
-
A.
\(\frac{A}{B} = \frac{{A \cdot M}}{{B \cdot M}}\,\,\left( {B,M \ne 0} \right)\).
-
B.
\(\frac{A}{B} = \frac{{A \cdot M}}{B}\,\,\left( {B,M \ne 0} \right)\).
-
C.
\(\frac{A}{B} = \frac{A}{{B \cdot M}}\,\,\left( {B,M \ne 0} \right)\).
-
D.
\(\frac{A}{B} = \frac{{A \cdot M}}{{B \cdot N}}\,\,\left( {B,M \ne 0,N \ne M} \right)\).
Bài 18 :
Sử dụng quy tắc đổi dấu, ta đưa phân thức \(\frac{{ - x - y}}{6}\) về dạng phân thức nào sau đây?
-
A.
\(\frac{{x - y}}{{ - 6}}\)
-
B.
\(\frac{{x + y}}{{ 6}}\)
-
C.
\(\frac{{x - y}}{{ 6}}\)
-
D.
\(\frac{{x + y}}{{ - 6}}\)
Bài 19 :
Dùng tính chất cơ bản của phân thức, chứng minh \(\frac{{{x^4} - 1}}{{x - 1}} = {x^3} + {x^2} + x + 1\)
Bài 20 :
Sử dụng tính chất cơ bản của phân thức và quy tắc đổi dấu, viết phân thức \(\frac{{24{x^2}{y^2}}}{{3x{y^5}}}\) thành một phân thức có mẫu là \( - {y^3}\) rồi tìm đa thức B trong đẳng thức \(\frac{{24{x^2}{y^2}}}{{3x{y^5}}} = \frac{B}{{ - {y^3}}}\)
Bài 21 :
Dùng tính chất cơ bản của phân thức, giải thích vì sao các kết luận sau đúng.
a) \(\frac{{{{(x - 2)}^3}}}{{{x^2} - 2x}} = \frac{{{{(x - 2)}^2}}}{x};\)
b) \(\frac{{1 - x}}{{ - 5x + 1}} = \frac{{x - 1}}{{5x - 1}}\).
Bài 22 :
Tìm đa thức thích hợp thay cho dấu “?”.
\(\frac{{y - x}}{{4 - x}} = \frac{?}{{x - 4}}\)
Bài 23 :
Trong các khẳng định sau, khẳng định sai là
-
A.
\(\frac{{5{x^2}y}}{{x{y^2}}} = \frac{{5x}}{y}\).
-
B.
\(\frac{{{x^3} - 8}}{{x - 2}} = {x^2} + 2x + 4\).
-
C.
\(\frac{{x - 5}}{{2 - x}} = \frac{{5 - x}}{{x - 2}}\).
-
D.
\(\frac{{3 - x}}{{x + 2}} = \frac{{x - 3}}{{x + 2}}\).













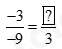





Danh sách bình luận