Cho hai đa thức \(A = {x^2} - xy + 2{y^2}\) và \(B = 2{x^2} + xy + {y^2}\)
a) Tìm đa thức C sao cho \(C = A + B\)
b) Tìm đa thức D sao cho \(D = A - B\)
c) Tìm đa thức E sao cho \(E = A.B\).
Áp dụng các phương pháp cộng, trừ, nhân đa thức để tìm được các đa thức C, D, E.
a)
\(\begin{array}{l}C = A + B\\C = \left( {{x^2} - xy + 2{y^2}} \right) + \left( {2{x^2} + xy + {y^2}} \right)\\C = \left( {{x^2} + 2{x^2}} \right) + \left( { - xy + xy} \right) + \left( {2{y^2} + {y^2}} \right)\\C = 3{x^2} + 3{y^2}\end{array}\)
b)
\(\begin{array}{l}D = A - B\\D = \left( {{x^2} - xy + 2{y^2}} \right) - \left( {2{x^2} + xy + {y^2}} \right)\\D = \left( {{x^2} - 2{x^2}} \right) + \left( { - xy - xy} \right) + \left( {2{y^2} - {y^2}} \right)\\D = - {x^2} - 2xy + {y^2}\end{array}\)
c)
\(\begin{array}{l}E = A.B\\E = \left( {{x^2} - xy + 2{y^2}} \right).\left( {2{x^2} + xy + {y^2}} \right)\\E = {x^2}.\left( {2{x^2} + xy + {y^2}} \right) - xy.\left( {2{x^2} + xy + {y^2}} \right) + 2{y^2}.\left( {2{x^2} + xy + {y^2}} \right)\\E = 2{x^4} + {x^3}y + {x^2}{y^2} - 2{x^3}y - {x^2}{y^2} - x{y^3} + 4{x^2}{y^2} + 2x{y^3} + 2{y^4}\\E = 2{x^4} + \left( {{x^3}y - 2{x^3}y} \right) + \left( {{x^2}{y^2} - {x^2}{y^2} + 4{x^2}{y^2}} \right) - x{y^3} + 2x{y^3} + 2{y^4}\\E = 2{x^4} - {x^3}y + 4{x^2}{y^2} - x{y^3} + 2x{y^3} + 2{y^4}\end{array}\)

Các bài tập cùng chuyên đề
Bài 1 :
Cho biểu thức \(3{x^3}\left( {{x^5} - {y^5}} \right) + {y^5}\left( {3{x^3} - {y^3}} \right)\)
a) Rút gọn biểu thức đã cho.
b) Tính giá trị của biểu thức đã cho nếu biết \({y^4} = {x^4}\sqrt 3 \).
Bài 2 :
Rút gọn biểu thức:
\(\dfrac{1}{4}\left( {2{x^2} + y} \right)\left( {x - 2{y^2}} \right) + \dfrac{1}{4}\left( {2{x^2} - y} \right)\left( {x + 2{y^2}} \right)\)
Bài 3 :
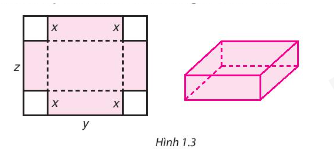
Bạn Thành dùng một miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) bằng cách cắt cắt bốn hình vuông cạnh x centimet ở bốn góc (H.1.3) rồi gấp lại. Biết rằng miếng bìa có chiều dài là y centimet, chiều rộng là z mét.
Tìm đa thức (ba biến x,y,z) biểu thị thể tích của chiếc hộp. Xác định bậc của đa thức đó.
Bài 4 :
Viết biểu thức tính khoảng cách giữa hai phương tiện trong tình hướng ở câu hỏi mở đầu:
Trên một đoạn sông thẳng, xuất phát cùng lúc từ một bến thuyền, thuyền đi xuôi dòng với tốc độ \(\left( {v + 3} \right)\)km/h, ca nô đi ngược dòng với tốc độ \(\left( {2v - 3} \right)\)km/h. Làm thế nào để tìm được quãng đường của mỗi phương tiện và khoảng cách giữa chúng sau khoảng thời gian \(t\) giờ kể từ khi rời bến?
Bài 5 :
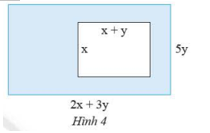
Tính diện tích phần tô màu trong Hình 4.
Bài 6 :
Các phép tính với đa thức nhiều biến thực hiện như thế nào?
Bài 7 :
a) Rút gọn rồi tính giá trị biểu thức:
\(P = \left( {5{{\rm{x}}^2} - 2{\rm{x}}y + {y^2}} \right) - \left( {{x^2} + {y^2}} \right) - \left( {4{{\rm{x}}^2} - 5{\rm{x}}y + 1} \right)\) khi x = 1,2 và x + y = 6,2
b) Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến a:
\(\left( {{x^2} - 5{\rm{x}} + 4} \right)\left( {2{\rm{x}} + 3} \right) - \left( {2{{\rm{x}}^2} - x - 10} \right)\left( {x - 3} \right)\)
Bài 8 :
Bạn Hạnh dự định cắt một miếng bìa có dạng tam giác vuông với độ dài hai cạnh góc vuông lần lượt là 6 (cm), 8 (cm). Sau khi xem xét lại, bạn Hạnh quyết định tăng độ dài cạnh góc vuông 6 (cm) thêm x (cm) và tăng độ dài cạnh góc vuông 8 (cm) thêm y(cm) (hình 2). Viết đa thức biểu thị diện tích phần tăng thêm của miếng bìa theo x và y.
Bài 9 :
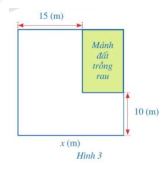
Khu vườn của nhà bác Xuân có dạng hình vuông. Bác Xuân muốn dành một mảnh đất có dạng hình chữ nhật ở góc khu vườn để trồng rau (hình 3). Biết diện tích của mảnh đất không trồng rau bằng 475 m2. Tính độ dài cạnh x (m) của khu vườn đó.
Bài 10 :
Thực hiện phép tính:
\(a) - \dfrac{1}{3}{a^2}b\left( { - 6{\rm{a}}{b^2} - 3{\rm{a}} + 9{b^3}} \right)\)
\(b)\left( {{a^2} + {b^2}} \right)\left( {{a^4} - {a^2}{b^2} + {b^4}} \right)\)
\(c)\left( { - 5{{\rm{x}}^3}{y^3}z} \right):\left( {\dfrac{{15}}{2}x{y^2}z} \right)\)
\(d)\left( {8{{\rm{x}}^4}{y^2} - 10{{\rm{x}}^2}{y^4} + 12{{\rm{x}}^3}{y^5}} \right):\left( { - 2{{\rm{x}}^2}{y^2}} \right)\)
Bài 11 :
Một mảnh vườn có dạng hình chữ nhật với chiều rộng là x (m), chiều dài là y (m).
a) Viết đa thức biểu thị diện tích của mảnh vườn
b) Nếu tăng chiều rộng thêm 2m và tăng chiều dài thêm 3 m thì được mảnh vườn mới. Viết đa thức biểu thị diện tích của mảnh vườn mới.
c) Viết đa thức biểu thị phần diện tích lớn hơn của mảnh vườn mới so với mảnh vườn ban đầu.
Bài 12 :
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:
\(\left( {1 + x} \right)\left( {1 + y} \right) - x\left( {y + 1} \right) - y + 9\)
Bài 13 :
Tìm ba số tự nhiên liên tiếp, biết tích của hai số sau lớn hơn tích của hai số đầu là \(16\).
Bài 14 :
Rút gọn biểu thức:
a) \(2x\left( {{x^2} + y} \right) - x\left( {2y + 1} \right) - x\left( {2{x^2} - 21y} \right)\)
b) \(5x\left( {6y - {x^2}} \right) + 3y\left( {y - 10x} \right) - 3y\left( {y - 1} \right) + 15{x^3}\)
c) \(18{x^{n + 1}}\left( {{y^{n + 1}} + {x^{n + 3}}} \right) + 9{y^3}\left( { - 2{x^{n + 1}}{y^{n - 2}} + 1} \right)\) với \(n\) là số tự nhiên lớn hơn 2.
Bài 15 :
Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến:
a) \(M = \left( {x - 1} \right)\left( {{x^2} + x + 1} \right) - {x^2}\left( {x - 1} \right) - {x^2} - 23\);
b) \(N = \left( {x - \frac{1}{2}y} \right)\left( {{x^2} + 2y} \right) - x\left( {{x^2} + 2y} \right) + y\left( {\frac{1}{2}{x^2} + y} \right) - \frac{1}{2}\).
Bài 16 :
Chứng minh rằng biểu thức \(P = \left( {2y - x} \right)\left( {x + y} \right) + x\left( {y - x} \right) - 2y\left( {x + 5y} \right) - 1\) luôn nhận giá trị âm với mọi giá trị của biến \(x\) và \(y\).
Bài 17 :
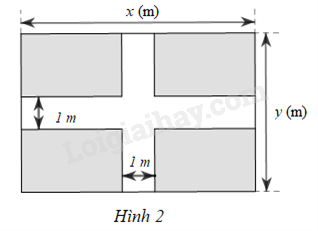
Một mảnh đất có dạng hình chữ nhật với chiều dài là \(x\)(m), chiều rộng là \(y\) (m) với \(1 < y < x\). Người ta để lối đi có độ rộng 1 (m) (phần không tô màu) như Hình 2.
a) Viết đa thức \(S\) biểu thị diện tích phần còn lại của mảnh đất đó.
b) Tính giá trị của \(S\) tại \(x = 9;y = 5,4\).
Bài 18 :
Tính:
a) \(3a\left( {a - b} \right) - b\left( {b - 3a} \right)\);
b) \(3{a^2}\left( {2a + b} \right) - 2b\left( {4{a^2} - b} \right)\);
c) \(\left( {a + b} \right)\left( {a - b} \right) - \left( {a - 1} \right)\left( {a - 2} \right)\);
d) \(b\left( {3{b^2} - {a^3}} \right) + \left( {{a^2} + 3b} \right)\left( {ab - {b^2}} \right)\).
Bài 19 :
Biết rằng \(x = a + b\) và \(y = 2a - b\). Tính các đa thức sau theo a và b.
a) \(A = 3x - 4y\);
b) \(B = 2xy\).
Bài 20 :
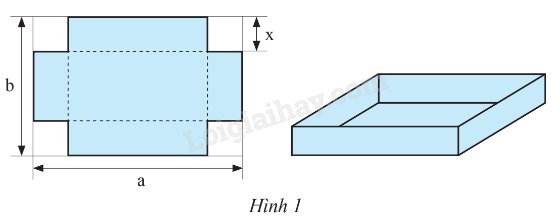
Từ một tấm tôn hình chữ nhật có chiều dài bằng a (cm), chiều rộng bằng b (cm), người ta cắt bỏ bốn hình vuông cạnh bằng x (cm) ở bốn góc, rồi gấp và hàn thành thùng không có nắp (Hình 1). Viết biểu thức biểu thị:
a) Thể tích nước tối đa mà thùng có thể chứa được.
b) Tổng diện tích của năm mặt của chiếc thùng.
Bài 21 :
Một hình lăng trụ đứng có đáy là một tam giác với ba cạnh 3x, 4x, và 5x ( biết rằng đó là một tam giác vuông), chiều cao của một hình lăng trụ bằng y ( \(x > 0,y > 0\)). Hãy tìm đa thức với hai biến x và y biểu thị diện tích toàn phần ( tổng diện tích xung quanh và diện tích hai đáy) của hình lăng trụ đó. Xác định bậc của đa thức tìm được.
Bài 22 :
Thực hiện phép tính:
a) \(7{x^2}{y^5} - \frac{7}{3}{y^2}\left( {3{x^2}{y^3} + 1} \right)\)
b) \(\frac{1}{2}x\left( {{x^2} + {y^2}} \right) - \frac{3}{2}{y^2}\left( {x + 1} \right) - \frac{1}{{\sqrt 4 }}{x^3}\)
c) \(\left( {x + y} \right)\left( {{x^2} + {y^2} + 3xy} \right) - {x^3} - {y^3}\)
d) \(\left( { - 132{x^{n + 2}}{y^{10}}{z^{n + 2}} + 143{x^{n + 2}}{y^{12}}{z^n}} \right):\left( {11{x^n}{y^9}{z^n}} \right)\) với \(n\) là số tự nhiên.
Bài 23 :
Cho \(a,b,c\) là ba số tùy ý. Chứng minh: Nếu \(a + b + c = 0\) thì \({a^3} + {b^3} + {c^3} = 3abc\)
Bài 24 :
Thu gọn các đa thức sau:
a) \(ab\left( {3a - 2b} \right) - ab\left( {3b - 2a} \right)\);
b) \(\left( {a - 4b} \right)\left( {a + 2b} \right) + a\left( {a + 2b} \right)\).
Bài 25 :
Lúc đầu người ta dự kiến thiết kế một chiếc hộp hình lập phương với độ dài mỗi cạnh là x (cm) \(\left( {x > 3} \right)\). Sau đó người ta điều chỉnh tăng chiều dài 3cm, giảm chiều rộng 3cm và giữ nguyên chiều cao. Sau khi điều chỉnh, thể tích của hộp giảm bao nhiêu, diện tích toàn phần của hộp giảm đi bao nhiêu so với dự kiến ban đầu? Áp dụng với \(x = 15cm\).
Bài 26 :
Rút gọn các biểu thức sau:
a. 2x(3x + 2) - 3x(2x + 3)
b. (x + 2)3 + (x - 3)2 - x2(x + 5)
c. (3x3 - 4x2 + 6x) : 3x
Bài 27 :
Thu gọn biểu thức:
a) \(\frac{3}{4}{x^3}{y^3}:\left( { - \frac{1}{2}{x^2}{y^2}} \right)\);
b) \(x\left( {x - y} \right) + y\left( {x + y} \right)\) ;
c) \(\left( {x + 3y} \right)\left( {x - 2y} \right) - \left( {{x^4}y - 6{x^2}{y^3}} \right):{x^2}y\).
Bài 28 :
Dạng rút gọn của biểu thức \(A = \left( {2x - 3} \right)\left( {4 + 6x} \right) - \left( {6 - 3x} \right)\left( {4x - 2} \right)\) là
-
A.
\(0\)
-
B.
\(40x\)
-
C.
\(-40x\)
-
D.
\(24x^{2}-40x\)
Bài 29 :
Thực hiện phép tính:
a) \(\left( {3xyz - 3{x^2} + 5xy - 1} \right) - \left( {5{x^2} + xyz - 5xy + 3 - y} \right)\)
b) \(\left( {3{x^3} - {x^2}y + 2xy + 3} \right) + \left( {{x^2}y - 2xy - 2} \right)\)
c) \(\left( {2x{y^3} - 4y - 8x} \right).\left( {\frac{1}{2}y} \right)\)
d) \(\left( {{x^8}{y^8} + 2{x^5}{y^5} + 7{x^3}{y^3}} \right):\left( { - {x^2}{y^2}} \right)\)
Bài 30 :
Chứng tỏ rằng giá trị của các biểu thức sau không phụ thuộc vào giá trị của biến \(x\).
a) \(P = x\left( {3x + 2} \right) - x\left( {{x^2} + 3x} \right) + {x^3} - 2x + 3\)
b) \(Q = x\left( {2x - 3} \right) + 6x\left( {\frac{1}{2} - \frac{1}{3}x} \right) + 1\)




















Danh sách bình luận