Cho \(a\) và \(b\) là hai số thực bất kì.
1. Thực hiện phép tính \({\left[ {a + \left( { - b} \right)} \right]^3}\).
2. Hãy cho biết: \({\left( {a - b} \right)^3} = ?\).
1. Ta nhân đa thức với đa thức kết hợp với sử dụng hằng đẳng thức bình phương của một hiệu: Lấy từng hạng tử của đa thức này nhân với từng hạng tử của đa thức kia.
2. Dựa vào kết quả từ ý 1.
1.Ta có:
\(\begin{array}{l}{\left[ {a + \left( { - b} \right)} \right]^3} = {\left( {a - b} \right)^2}\left( {a - b} \right) = \left( {{a^2} - 2ab + {b^2}} \right)\left( {a - b} \right)\\ = {a^3} - 2{a^2}b + a{b^2} + 2a{b^2} - {a^2}b - {b^3}\\ = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}\end{array}\)
2. \({\left( {a - b} \right)^3} = {a^3} - 3{a^2}b + 3a{b^2} - {b^3}.\)
Các bài tập cùng chuyên đề
Với hai số \(a,b\) bất kì, viết \(a - b = a + \left( { - b} \right)\) và áp dụng hằng đẳng thức lập phương của một tổng để tính \({\left( {a - b} \right)^3}\).
Từ đó rút ra liên hệ giữa \({\left( {a - b} \right)^3}\) và \({a^3} - 3{a^2}b + 3a{b^2} - {b^3}\).
Khai triển \({\left( {2x - y} \right)^3}\)
Viết biểu thức sau dưới dạng lập phương của một hiệu
\(8{x^3} - 36{x^2}y + 54x{y^2} - 27{y^3}\).
Chứng minh \({\left( {a - b} \right)^3} = - {\left( {b - a} \right)^3}\)
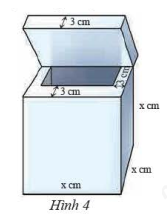
Một thùng chứa dạng hình lập phương có độ dài cạnh bằng \(x\) (cm). Phần vỏ bao gồm nắp có độ dày \(3\)cm. Tính dung tích (sức chứa) của thùng, viết kết quả dưới dạng đa thức.
Viết biểu thức sau dưới dạng lập phương của một hiệu:
\(8{{\rm{x}}^3} - 36{{\rm{x}}^2}y + 54{\rm{x}}{y^2} - 27{y^3}\)
Tính nhanh: \({101^3} - {3.101^2} + 3.101 - 1\).
Tính:
a) \({\left( {a - 3} \right)^3};\)
b) \({\left( {3u - 4v} \right)^3}.\)
a) Viết biểu thức \({x^3} - 6{x^2} + 12x - 8\) dưới dạng lập phương của một hiệu.
b) Sử dụng kết quả của câu a, hãy tính giá trị của biểu thức sau tại \(x = 12:\)
\({x^3} - 6{x^2} + 12x - 8\)
Khai triển (2x – 1)3 được biểu thức:
A. 8x3 + 12x2 + 6x + 1.
B. 8x3 + 6x2 + 12x + 1.
C. 8x3 – 12x2 + 6x – 1.
D. 8x3 – 6x2 + 12x – 1.
Chứng minh \({\left( {a - b} \right)^3} = - {\left( {b - a} \right)^3}\).
Tính nhanh \({102^3} - {6.102^2} + 12.102 - 8\).
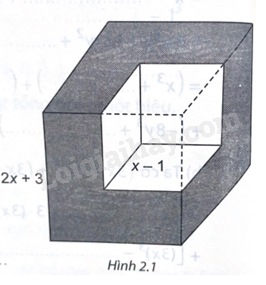
Từ một khối lập phương có độ dài cạnh là \(2x + 3\) (cm), ta cắt bỏ một khối lập phương có độ dài \(x-1\) (cm) (H.2.1). Tính thể tích phần còn lại, viết kết quả dưới dạng đa thức.
Khai triển hằng đẳng thức: \((x−y)^3\)
