Đề bài

Tính tích của hai đa thức \(G = {x^2} - 3y + 8\) và \(H = {y^2} - 2x\)

Phương pháp giải

Sử dụng phương pháp nhân đa thức với đa thức: ta nhân mỗi hạng tử của đa thức này với từng hạng tử của đa thức kia rồi cộng các kết quả lại với nhau.

Lời giải của GV Loigiaihay.com

Ta có

\(\begin{array}{l}G.H = \left( {{x^2} - 3y + 8} \right).\left( {{y^2} - 2x} \right)\\ = {x^2}.\left( {{y^2} - 2x} \right) - 3y.\left( {{y^2} - 2x} \right) + 8.\left( {{y^2} - 2x} \right)\\ = {x^2}{y^2} - 2{x^3} - 3{y^3} + 6xy + 8{y^2} - 16x\end{array}\)

Xem thêm : SGK Toán 8 - Cùng khám phá

Báo lỗi - Góp ý

BÌNH LUẬN

Danh sách bình luận

Đang tải bình luận...

Các bài tập cùng chuyên đề

Bài 1 :

Chọn câu đúng.

A.
\(\left( {{x^2} - 1} \right)\left( {{x^2} + 2x} \right) = {x^4} - {x^3} - 2x\).
B.
\(\left( {{x^2} - 1} \right)\left( {{x^2} + 2x} \right) = {x^4} - {x^2} - 2x\).
C.
\(\left( {{x^2} - 1} \right)\left( {{x^2} + 2x} \right) = {x^4} + 2{x^3} - {x^2} - 2x\).
D.
\(\left( {{x^2} - 1} \right)\left( {{x^2} + 2x} \right) = {x^4} + 2{x^3} - 2x\).

Xem lời giải >>

Bài 2 :

Hãy nhớ lại quy tắc nhân hai đa thức một biến bằng cách thực hiện phép nhân:

\(\left( {2x + 3} \right).\left( {{x^2} - 5x + 4} \right)\)

Xem lời giải >>

Bài 3 :

Bằng cách tương tự, hãy làm phép nhân \(\left( {2x + 3y} \right).\left( {{x^2} - 5xy + 4{y^2}} \right)\).

Xem lời giải >>

Bài 4 :

Thực hiện phép nhân:

a) \(\left( {2x + y} \right)\left( {4{x^2} - 2xy + {y^2}} \right)\);

b) \(\left( {{x^2}{y^2} - 3} \right)\left( {3 + {x^2}{y^2}} \right)\).

Xem lời giải >>

Bài 5 :

Xét biểu thức đại số với hai biến k và m sau:

\(P = \left( {2k - 3} \right)\left( {3m - 2} \right) - \left( {3k - 2} \right)\left( {2m - 3} \right)\)

a) Rút gọn biểu thức P.

b) Chứng minh rằng tại mọi giá trị nguyên của k và m, giá trị của biểu thức P luôn là một số nguyên chia hết cho 5.

Xem lời giải >>

Bài 6 :

Làm tính nhân:

a) \(\left( {{x^2} - xy + 1} \right)\left( {xy + 3} \right)\)

b) \(\left( {{x^2}{y^2} - \dfrac{1}{2}xy + 2} \right)\left( {x - 2y} \right)\)

Xem lời giải >>

Bài 7 :

Chứng minh đẳng thức sau: \(\left( {2x + y} \right)\left( {2{x^2} + xy - {y^2}} \right) = \left( {2x - y} \right)\left( {2{x^2} + 3xy + {y^2}} \right)\).

Xem lời giải >>

Bài 8 :

Bà Khanh dự định mua x hộp sữa, mỗi hộp giá y đồng. Nhưng khi đến cửa hàng, bà Khanh thấy giá sữa giảm 1 500 đồng mỗi hộp nên quyết định mua thêm 3 hộp nữa.

Tìm đa thức biểu thị số tiền bà Khanh phải trả cho tổng số hộp sữa đã mua.

Xem lời giải >>

Bài 9 :

Bà Khanh dự định mua x hộp sữa, mỗi hộp giá y đồng. Nhưng khi đến cửa hàng, bà Khanh thấy giá sữa giảm 1 500 đồng mỗi hộp nên quyết định mua thêm 3 hộp nữa.

Tìm đa thức biểu thị số tiền bà Khanh phải trả cho tổng số hộp sữa đã mua.

Xem lời giải >>

Bài 10 :

Thực hiện các phép nhân:

a) \(\left( { - 5{a^4}} \right)\left( {{a^2}b - a{b^2}} \right)\)

b) \(\left( {x + 2y} \right)\left( {x{y^2} - 2{y^3}} \right)\)

Xem lời giải >>

Bài 11 :

Thực hiện các phép nhân:

a) \(\left( {x - y} \right)\left( {x - 5y} \right)\)

b) \(\left( {2x + y} \right)\left( {4{x^2} - 2xy + {y^2}} \right)\)

Xem lời giải >>

Bài 12 :

Kết quả của phép nhân \((x + y - 1)(x + y + 1)\) là:

A. \({x^2} - 2xy + {y^2} + 1\)

B. \({x^2} + 2xy + {y^2} - 1\)

C. \({x^2} - 2xy + {y^2} - 1\)

D. \({x^2} + 2xy + {y^2} + 1\)

Xem lời giải >>

Bài 13 :

Kết quả của phép nhân \((2x + 1)(4{x^2} - 2x + 1)\) là:

A. \(8{x^3} - 1\)

B. \(4{x^3} + 1\)

C. \(8{x^3} + 1\)

D. \(2{x^2} + 1\)

Xem lời giải >>

Bài 14 :

Thực hiện các phép tính sau:

a) \({x^2}y\left( {5xy - 2{x^2}y - {y^2}} \right)\)

b) \(\left( {x - 2y} \right)\left( {2{x^2} + 4xy} \right)\)

Xem lời giải >>

Bài 15 :

a) Tính tích: \(\left( {x + 1} \right).\left( {{x^2} - x + 1} \right)\)

b) Nêu quy tắc nhân hai đa thức trong trường hợp một biến.

Xem lời giải >>

Bài 16 :

Tính: \({\left( {x - y} \right)}{\left( {x - y} \right)}\)

Xem lời giải >>

Bài 17 :

Giải thích vì sao ta có thể viết:

\(\left( {x + 2y} \right).\left( {2x - y} \right) = x.2x + y.\left( { - y} \right) + 2y.2x + 2y.\left( { - y} \right) = 2{x^2} - xy + 4xy - 2{y^2} = 2{x^2} + 3xy - 2{y^2}\)

Xem lời giải >>

Bài 18 :

Trong phần Khởi động, hãy tính diện tích của phần được tô màu trong Hình 1.5 theo \(x\) và \(y\).

Xem lời giải >>

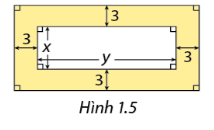
Bài 19 :

Thực hiện các phép tính sau:

a) \(\left( {x - 4} \right)\left( {{y^3} + 2y - 3} \right)\);

b) \(\left( {{x^2} - xy + {y^2}} \right)\left( {x + y} \right)\)

Xem lời giải >>

Bài 20 :

Thực hiện các phép nhân:

a) \(\left( {x + 3y} \right)\left( {x - 2y} \right)\);

b) \(\left( {2x - y} \right)\left( {y - 5x} \right)\);

c) \(\left( {2x - 5y} \right)\left( {{y^2} - 2xy} \right)\);

d) \(\left( {x - y} \right)\left( {{x^2} - xy - {y^2}} \right)\).

Xem lời giải >>

Bài 21 :

Thực hiện phép tính:

a) \(\left( {x - 2y} \right)\left( {{x^2}z + 2xyz + 4{y^2}z} \right)\)

b) \(\left( {{x^2} - \frac{1}{3}xy + \frac{1}{9}{y^2}} \right)\left( {x + \frac{1}{3}y} \right)\).

Xem lời giải >>

Bài 22 :

Tìm tích của hai đa thức:

a) \(2{x^4} - {x^3}y + 6x{y^3} + 2{y^4}\) và \({x^4} + 3{x^3}y - {y^4}\);

b) \({x^3}y + 0,4{x^2}{y^2} - x{y^3}\) và \(5{x^2} - 2,5xy + 5{y^2}\).

Xem lời giải >>

Bài 23 :

Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến:

\(P = {x^4} - \left( {x - y} \right)\left( {x + y} \right)\left( {{x^2} + {y^2}} \right) - {y^4}\).

Xem lời giải >>

Bài 24 :

Rút gọn biểu thức:

a) \(\left( {x - y} \right)\left( {y + z} \right)\left( {z + x} \right) + \left( {x + y} \right)\left( {y - z} \right)\left( {z + x} \right) + \left( {x + y} \right)\left( {y + z} \right)\left( {z - x} \right)\);

b) \(\left( {2x + y} \right)\left( {2y + z} \right)\left( {2z + x} \right) - \left( {2x - y} \right)\left( {2y - z} \right)\left( {2z - x} \right)\).

Xem lời giải >>

Bài 25 :

Tích của một đa thức bậc 3 và một đa thức bậc 2 là một đa thức

A. bậc 5.

B. bậc 6.

C. bậc nhỏ hơn 5.

D. bậc lớn hơn 6.

Xem lời giải >>

Bài 26 :

Thu gọn các tích \(A = \left( {{x^2}y + x{y^2}} \right)\left( {{x^2} - xy + {y^2}} \right)\) và \(B = \left( {x - y} \right)\left( {{x^3}y + {x^2}{y^2} + x{y^3}} \right)\), ta được:

A. \(A = {x^4}y - x{y^4}\) và \(B = {x^4}y + x{y^4}\).

B. \(A = {x^4}y + x{y^4}\) và \(B = {x^4}y - x{y^4}\).

C. \(A = x{y^4} - {x^4}y\) và \(B = {x^4}y + x{y^4}\).

D. \(A = {x^4}y + x{y^4}\) và \(B = x{y^4} - {x^4}y\).

Xem lời giải >>

Bài 27 :

Thực hiện phép nhân

a) \(\frac{2}{5}{x^2}y\left( {5{x^2}y - 10x{y^2} + 2{y^3}} \right)\);

b) \(\left( {{x^2} - 2xy} \right)\left( {{x^3} + 3{x^2}y - 5x{y^2} - {y^3}} \right)\).

Xem lời giải >>

Bài 28 :

Một chiếc khăn trải bàn có dạng hình chữ nhật \(ABCD\) được thêu một họa tiết có dạng hình thoi \(MNPQ\) ở giữa với \(MP = x\left( {cm} \right);NQ = y\left( {cm} \right)\left( {x > y > 0} \right)\) như Hình 5. Viết đa thức biểu thị diện tích phần còn lại của chiếc khan trải bàn đó.

Xem lời giải >>

Bài 29 :

Làm tính nhân:

a) \(\left( {{x^2}\;-xy + 1} \right)\left( {xy + 3} \right)\).

b) \(\left( {{x^2}{y^2} - \frac{1}{2}xy + 2} \right)\left( {x - 2y} \right)\).

Xem lời giải >>

Bài 30 :

Rút gọn biểu thức sau đây để thấy rằng giá trị của nó không phụ thuộc vào giá trị của biến: \(\left( {x-5} \right)\left( {2x + 3} \right)-2x\left( {x-3} \right) + x + 7\).

Xem lời giải >>