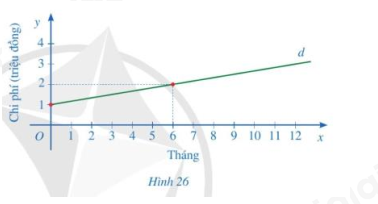
Để sử dụng dịch vụ truyền hình cáp, người dùng phải trả một khoản phí ban đầu và phí thuê bao hằng tháng. Một phần đường thẳng d ở hình 26 biểu thị tổng chi phí (đơn vị: triệu đồng) để sử dụng dịch vụ truyền hình cáp theo thời gian sử dụng của một gia đình (đơn vị: tháng).
a) Tìm hàm số bậc nhất sao cho đồ thị của hàm số là đường thẳng d.
b) Giao điểm của đường thẳng d với trục tung trong tình huống này có ý nghĩa gì?
c) Tính tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng.
Gọi hàm số bậc nhất là y = ax + b (a\( \ne \)0)
Quan sát hình 26 để xác định a, b
a) Gọi hàm số bậc nhất của đường thẳng d là y = ax + b (a\( \ne \)0)
Từ hình 26, ta thấy đường thẳng d đi qua hai điểm (0; 1) và (6; 2)
Thay tọa độ điểm (0; 1) vào hàm số y = ax + b ta được:
1 = a. 0 + b suy ra b = 1
Hàm số bậc nhất là y = ax + 1 (a\( \ne \)0) (1)
Vì đường thẳng d đi qua điểm (6; 2) nên thay tọa độ điểm (6; 2) vào hàm số (1) ta được là:
2 = a. 6 + 1 suy ra \(a = \dfrac{1}{6}\)
Vậy hàm số của đường thẳng d là \(y = \dfrac{1}{6}x + 1\)
b) Giao điểm của đường thẳng d với trục tung là 1 trong tình huống này có nghĩa là người dùng phải trả khoản phí bạn đầu là 1 triệu đồng
c) Tổng chi phí mà gia đình phải trả khi sử dụng dịch vụ truyền hình với thời gian 12 tháng là ta thay x = 12 vào hàm số \(y = \dfrac{1}{6}x + 1\)
Khi đó: \(y = \dfrac{1}{6}.12 + 1 = 3\)
Tổng chi phí mà gia đình đó phải trả khi sử dụng dịch vụ truyền hình cáp với thời gian 12 tháng là 3 triệu đồng.

Các bài tập cùng chuyên đề
Bài 1 :
Cho hai hàm số bậc nhất : \({d_1}\): y = 2x - 3 và \({d_2}\): y = x – 2 .
a) Vẽ đồ thị các hàm số trên cùng một mặt phẳng tọa độ Oxy.
b) Tìm tọa độ giao điểm của hai đồ thị hàm số trên.
c) Xác định a, b của hàm số bậc nhất y = ax + b, (a \( \ne \) 0) biết rằng đồ thị hàm số \({d_3}\) của hàm số y = ax + b song song với \({d_1}\) và cắt đường thẳng \({d_2}\) tại B có hoành độ bằng -1.
Bài 2 :
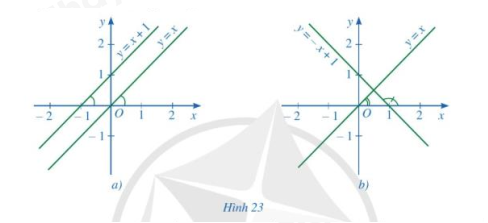
a) Quan sát hình 23a, tìm hệ số góc của hai đường thẳng y = x và y = x + 1 và nêu vị trí tương đối của hai đường thẳng đó.
b) Quan sát hình 23b, tìm hệ số góc của hai đường thẳng y = x và y = -x + 1 và nêu vị trí tương đối của hai đường thẳng đó.
Bài 3 :
Xét vị trí tương đối của hai đường thẳng y = -5x và y = -5x +2
Bài 4 :
Chỉ ra các cặp đường thẳng cắt nhau và các cặp đường thẳng song song trong số các đường thẳng sau:
y = -2x + 5; y = -2x; y = 4x -1
Bài 5 :
Xác định đường thẳng y = ax + b \(\left( {a \ne 0} \right)\)có hệ số góc bằng -1 và đi qua điểm M (1; 2). Sau đó vẽ đường thẳng tìm được trên mặt phẳng tọa độ.
Bài 6 :
Trong các phát biểu sau, phát biểu nào đúng, phát biểu nào sai về hai đường thẳng
d: \(y = {\rm{ax + b}}\left( {a \ne 0} \right)\) và d’: \(y = a'x + b'\left( {a' \ne 0} \right)\)?
a) Nếu hai đường thẳng d và d’ song song với nhau thì a = a’; b \( \ne \) b’
b) Nếu hai đường thẳng d và d’ song song với nhau thì a = a’; b = b’
c) Nếu hai đường thẳng d và d’ cắt nhau thì \(a \ne a'\)
d) Nếu hai đường thẳng d và d’ cắt nhau thì \(a \ne a'\), \(b \ne b'\)
Bài 7 :
Tìm hàm số bậc nhất y = ax + b (a\( \ne \)0) trong mỗi trường hợp sau:
a) Đồ thị của hàm số đó đi qua điểm M (1; 3) và có hệ số góc bằng -2.
b) Đồ thị của hàm số đó đi qua điểm N (-1; 4) và song song với đường thẳng y = -3x – 1.
Bài 8 :
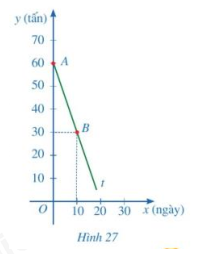
Một kho chứa 60 tấn xi măng, mỗi ngày đều xuất đi m(tấn) với 0<m<60. Gọi y (tấn ) là khối lượng xi măng còn lại trong kho sau x ngày xuất hàng.
a) Chứng tỏ rằng y là hàm số bậc nhất của biến x, tức là y = ax + b (\(a \ne 0\)).
b) Trong hình 27, tia At là một phần đường thẳng y = ax + b. Tìm a, b. Từ đó hãy cho biết trong kho còn lại bao nhiêu tấn xi măng sau 15 ngày.
Bài 9 :
Cho hai đường thẳng \(d:y = mx - \left( {2m + 2} \right)\) và \(d':y = \left( {3 - 2m} \right)x + 1\) với \(m \ne 0\) và \(m \ne - \frac{3}{2}\)
a) Tìm giá trị của \(m\) để đường thẳng \(d\) đi qua điểm \(A\left( {1;1} \right)\)
b) Gọi \(\beta \) là góc tạo bởi đường thẳng \(d\) ở câu a và trục \(Ox\). Hỏi \(\beta \) là góc nhọn hay góc tù? Tại sao?
c) Tìm giá trị của \(m\) để \(d\) cắt \(d'\).
Bài 10 :
Cho đường thẳng \(d:y = \left( {m - \frac{1}{2}} \right)x + 2m - 2\) với \(m \ne \frac{1}{2}\). Tìm giá trị của \(m\) để:
a) Đường thẳng \(d\) song song với đường thẳng \({d_1}:y = \frac{1}{2}mx - 2\) với \(m \ne 0\);
b) Đường thẳng \(d\) trùng với đường thẳng \({d_2}:y = x - \frac{2}{3}m + 2\);
c) Đường thẳng \(d\) và đường thẳng \({d_3}:y = \sqrt 2 x - m + 2\) cắt nhau tại một điểm nằm trên trục \(Oy\).
Bài 11 :
Cho hai đường thẳng y=2x-1 và y=x-3. Bằng cách so sánh hai hệ số góc, hãy cho biết hai đường thẳng này có song song hay trùng nhau không
Bài 12 :
Cho hai hàm số bậc nhất y=2mx+1 và y=(m−1)x+2. Tìm các giá trị của m để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau
b) Hai đường thẳng cắt nhau
Bài 13 :
Vuông: Làm thế nào để biết hai đường thẳng \(y = {\rm{ax + b}}\) và \(y = a'x + b'\) song song hay cắt nhau nhỉ?
Tròn: Cứ vẽ hai đường thẳng này trong cùng một mặt phẳng tọa độ Oxy là biết ngay mà.
Pi: Anh có một cách nhanh hơn nhiều mà không cần vẽ hình. Trong bài học này chúng ta sẽ cùng tìm hiểu nhé.
Em hãy trình bày cách làm của Pi để trả lời câu hỏi của bạn Vuông
Bài 14 :
Hãy chỉ ra cặp đường thẳng song song với nhau và các cặp đường thẳng cắt nhau trong các đường thẳng sau
y=−x+1; y=−2x+1;
y=−2x+2; y=−x
Bài 15 :
Cho hàm số bậc nhất y=mx−5 và y=(2m+1)x+3. Tìm các giá trị của m để đồ thị của hai hàm số là:
a) Hai đường thẳng song song
b) Hai đường thẳng cắt nhau
Bài 16 :
Trong mặt phẳng tọa độ Oxy, cho hai đường thẳng y=x và y=−x+2
a) Vẽ hai đường thẳng đã cho trên cùng một mặt phẳng tọa độ
b) Tìm giao điểm A của hai đường thẳng đã cho
c) Gọi B là giao điểm của đường thẳng y=−x+2 và trục Ox. Chứng minh tam giác OAB vuông tại A, tức hai đường thẳng y=x và y=−x+2 vuông góc với nhau
d) Có nhận xét gì về tích hai hệ số góc của hai đường thẳng đã cho
Bài 17 :
Cho hàm số bậc nhất y=(m+2)x+3
a) Tìm m để đồ thị hàm số song song với đường thẳng y=−x
b) Vẽ đồ thị hàm số với giá trị m tìm được ở câu a
c) Tìm giao điểm A của đồ thị hàm số tìm được ở câu a và đồ thị của hàm số y=x+1. Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số y=x+1 với trục Ox
Bài 18 :
Với giá trị nào của m, đường thẳng y=mx+1 (m≠0)
a) Song song với đường thẳng y=3x
b) Cắt trục hoành tại điểm có hoành độ bằng -2
c) Đồng quy với các đường thẳng y=5x−2 và y=−x+4 (tức là ba đường thẳng này cắt nhau tại một điểm) Với giá trị m tìm được, hãy vẽ ba đường thẳng này trên cùng một hệ trục tọa độ để kiểm nghiệm kết quả.
Bài 19 :
Khi nào thì hai đường thẳng \(y = ax + b\left( {a \ne 0} \right)\) và \(y = a'x + b'\left( {a' \ne 0} \right)\) song song với nhau, trùng nhau, cắt nhau?
Bài 20 :
Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:
\({d_1}:y = 3x\); \({d_2}:y = - 7x + 9\);
\({d_3}:y = 3x - 0,8\); \({d_4}:y = - 7x - 1\);
\({d_5}:y = \sqrt 2 x + 10\); \({d_6}:y = \sqrt 2 x + \sqrt {10} \)
Bài 21 :
Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:
\({d_1}:y = 0,2x\); \({d_2}:y = - 2x + 4\); \({d_3}:y = 0,2x - 0,8\); \({d_4}:y = - 2x - 5\); \({d_5}:y = \sqrt 3 x + 3\); \({d_6}:y = \sqrt 3 x - \sqrt 5 \).
Bài 22 :
Cho hai hàm số bậc nhất \(y = 2mx - 5\) và \(y = 2x + 1\).
Với giá trị nào của \(m\) thì đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau?
b) Hai đường thẳng cắt nhau?
Bài 23 :
Cho hai hàm số bậc nhất \(y = mx - 3\) và \(y = 5x + n\). Tìm giá trị của m và n để đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song
b) Hai đường thẳng cắt nhau.
Bài 24 :
Các cặp đường thẳng sau song song hay cắt nhau? Giải thích vì sao.
a) \(d:y = 3x + 5\) và \(d':y = 3x - 2\)
b) \(d:y = \frac{4}{3}x - \frac{1}{2}\) và \(d':y = \frac{3}{4}x + \frac{5}{4}\)
Bài 25 :
a) Xác định hệ số góc của các đường thẳng sau:
\(\begin{array}{l}{d_1}:y = 1,5 - 2x\\{d_2}:y = 3\left( {1 - x} \right) + 2x\end{array}\)
b) Đường thẳng \({d_3}:y = - x + 2\) song song hay cắt đường thẳng \({d_1},{d_2}\)? Giải thích.
Bài 26 :
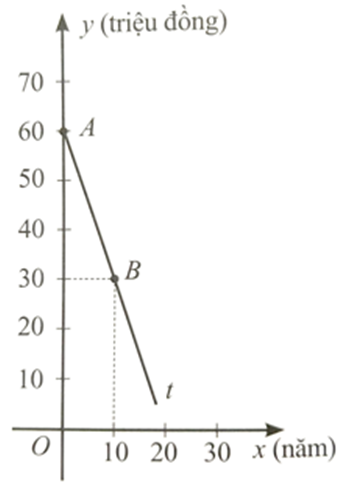
Một thiết bị tiệt khuẩn y tế bằng năng lượng mặt trời được mua với giá 60 triệu đồng, mỗi năm thiết bị tiệt khuẩn đó đều khấu hao \(k\) (triệu đồng) với \(0 < k < 60\). Gọi \(y\) (triệu đồng) là giá của thiết bị tiệt khuẩn đó sau \(x\) năm sử dụng.
a) Chứng tỏ rằng y là hàm số bậc nhất của \(x\), tức là \(y = ax + b, (a≠0)\)
b) Trong hình vẽ bên, tia \(At\) là một phần của đường thẳng \(y = ax + b\). Tìm \(a, b\). Từ đó, cho biết sau 12 năm sử dụng thì giá của thiết bị tiệt khuẩn đó bằng bao nhiêu phần trăm so với giá mua ban đầu.
Bài 27 :
Đồ thị của hai hàm số \(y = x + 2\) và \(y = x + 1\)
-
A.
cắt nhau.
-
B.
trùng nhau.
-
C.
song song với nhau.
-
D.
Cả A, B, C đều sai.
Bài 28 :
Cho hàm số \(y = \left( {m - 1} \right)x + m\) (\(m\) là tham số \(m \ne 1\)) có đồ thị là đường thẳng \(\left( d \right)\).
a) Tìm \(m\) để \(\left( d \right):y = \left( {m - 1} \right)x + m\) song song với \(\left( {d'} \right):y = 2x - 3\).
b) Vẽ \(\left( d \right)\) với \(m\) tìm được và vẽ \(\left( {d'} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\).
c) Tìm \(m\) để đường thẳng \(y = \left( {m - 1} \right)x + m\) và hai đường thẳng \(y = x + 2;\,y = \frac{1}{2}x + 3\) đồng quy.
Bài 29 :
Xác định \(a,\,b\) của hàm số \(y = ax + b\,\left( {a \ne 0} \right)\) sao cho đồ thị hàm số:
a) Đi qua điểm \(A\left( {3;\, - 1} \right)\) và \(B = \left( {2;\, - 5} \right)\)
b) Đi qua giao điểm của hai đường thẳng \(\left( {{d_1}} \right):y = x + 1\) và \(\left( {{d_2}} \right):y = 2x - 3\), và đồ thị hàm số song song với đường thẳng \(y = \frac{3}{2}x - 24\).
c) Vuông góc với đường thẳng \(y = - \frac{1}{4}x + 9\) và cắt trục tung tại điểm có tung độ bằng \(5\)
Bài 30 :
Cho hai hàm số \(y = 2mx + 11\) và \(y = \left( {1 - m} \right)x + 2\). Với giá trị nào của m thì đồ thị của hai hàm số đã cho là:
a) Hai đường thẳng song song với nhau?
b) Hai đường thẳng cắt nhau?


















Danh sách bình luận