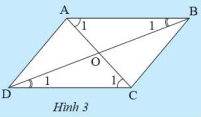
Cho tứ giác \(ABCD\) có các cạnh đối song song. Gọi \(O\) là giao điểm của hai đường chéo. Hãy chứng tỏ:
- Tam giác \(ABC\) bằng tam giác \(CDA\)
- Tam giác \(OAB\) bằng tam giác \(OCD\)
Áp dụng tính chất của hai đường thẳng song song
Áp dụng trường hợp bằng nhau thứ 2 của tam giác
Xét \(\Delta ABC\) và \(\Delta CDA\) ta có:
\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))
\(AC\) chung
\(\widehat {{\rm{ACB}}} = \widehat {{\rm{CAD}}}\) (do \(AD\) // \(BC\))
Suy ra: \(\Delta ABC = \Delta CDA\) (c-g-c)
Xét \(\Delta OAB\) và \(\Delta OCD\) ta có:
\(\widehat {{{\rm{A}}_{\rm{1}}}} = \widehat {{{\rm{C}}_{\rm{1}}}}\) (do \(AB\) // \(CD\))
AB = CD (do \(\Delta ABC = \Delta CDA\))
\(\widehat {{{\rm{B}}_{\rm{1}}}} = \widehat {{{\rm{D}}_{\rm{1}}}}\) (do \(\Delta ABC = \Delta CDA\))
Suy ra: \(\Delta OAB = \Delta OCD\) (g-c-g)

Các bài tập cùng chuyên đề
Bài 1 :
Chu vi của hình bình hành ABCD bằng 10 cm, chu vi của tam giác ABD bằng
9 cm. Khi đó độ dài BD là:
-
A.
4 cm
-
B.
6 cm
-
C.
2 cm
-
D.
1 cm
Bài 2 :
Vẽ hình bình hành, biết hai cạnh liên tiếp bằng 3 cm, 4 cm và góc xen giữa hai cạnh đó bằng 60o. Hãy mô tả cách vẽ và giải thích tại sao hình vẽ được là hình bình hành.
Bài 3 :
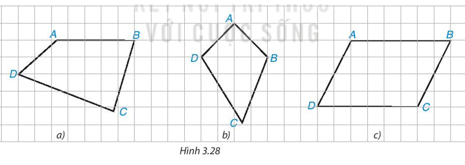
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
Bài 4 :
Trong Hình 3.28, có một hình bình hành. Đó là hình nào? Em có thể giải thích tại sao không?
Bài 5 :
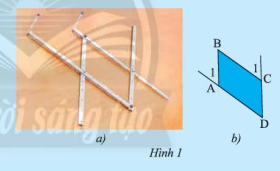
Hình 1a là hình ảnh của một thước vẽ truyền dùng để phóng to hay thu nhỏ một hình vẽ có sẵn. Dùng thước đo góc để đo số đo của các cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) của tứ giác \(ABCD\) (Hình 1b) rồi rút ra nhận xét về mối quan hệ giữa các cặp cạnh \(AB\) và \(CD\); \(AD\) và \(BC\).
Bài 6 :
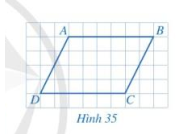
Cho biết các cặp cạnh đối AB và CD, AD và BC của tứ giác ABCD ở Hình 35 có song song với nhau hay không?


















Danh sách bình luận