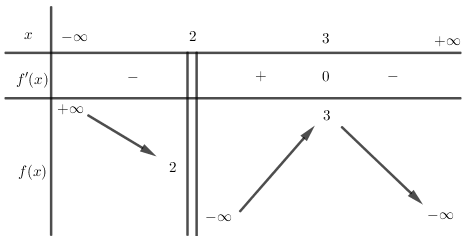
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ, chọn kết luận đúng:
-
A.
Hàm số đồng biến trên (−∞;3)
-
B.
Hàm số đồng biến trên (2;3).
-
C.
Hàm số nghịch biến trên (−∞;3).
-
D.
Hàm số nghịch biến trên (2;+∞)
Sử dụng định lý:
Định lý: Cho hàm số y=f(x) xác định và có đạo hàm trên K.
a) Nếu f′(x)>0,∀x∈K thì hàm số y=f(x) đồng biến trên K.
b) Nếu f′(x)<0,∀x∈K thì hàm số y=f(x) nghịch biến trên K.
Từ bảng biến thiên ta thấy: f′(x)>0 trên (2;3) nên hàm số đồng biến trên (2;3).
f′(x)<0 trên (−∞;2) và (3;+∞) nên hàm số nghịch biến trên các khoảng (−∞;2) và (3;+∞).
Đáp án : B

Các bài tập cùng chuyên đề
Cho hàm số y=f(x) đồng biến trên D và x1,x2∈D mà x1>x2, khi đó:
Cho hàm số f(x) xác định và có đạo hàm trên (a;b). Nếu f′(x)<0,∀x∈(a;b) thì:
Cho hàm số y=f(x) nghịch biến và có đạo hàm trên (−5;5). Khi đó:
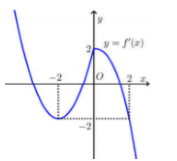
Hình dưới là đồ thị hàm số y=f′(x). Hỏi hàm số y=f(x) đồng biến trên khoảng nào dưới đây?
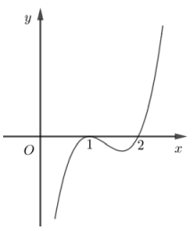
Cho hàm số y=f(x) xác định và liên tục trên R và có đạo hàm f′(x)=x2−4. Chọn khẳng định đúng:
Trong các hàm số dưới đây, hàm số nào không đồng biến trên R?
Cho hàm số y=f(x) xác định và có đạo hàm trên (a;b). Chọn kết luận đúng:
Cho hàm số y=f(x) xác định và có đạo hàm f′(x)=2x2 trên R. Chọn kết luận đúng:
Cho hàm số y=f(x) có bảng biến thiên như sau:
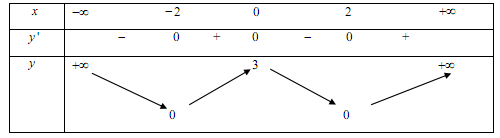
Khẳng định nào sau đây là khẳng định đúng:
Hàm số y=−x4−2x2+3 nghịch biến trên:
Cho hàm số: f(x)=−2x3+3x2+12x−5. Trong các mệnh đề sau, tìm mệnh đề sai?
Hàm số y=x3−3x2+4 đồng biến trên:
Trong tất cả các giá trị của tham số m để hàm số y=13x3+mx2−mx−m đồng biến trên R, giá trị nhỏ nhất của m là:
Tìm các giá trị của tham số m sao cho hàm số y=−x3−x2+mx+1 nghịch biến trên R?
Xác định giá trị của tham số m để hàm số y=x3−3mx2−m nghịch biến trên khoảng (0;1).
Tìm m để hàm số y=x33−2mx2+4mx+2 nghịch biến trên khoảng (−2;0).
Tìm tất cả các giá trị thực của tham số m để hàm số y=mx+22x+m nghịch biến trên từng khoảng xác định của nó?
Bất phương trình √2x3+3x2+6x+16−√4−x⩾ có tập nghiệm là \left[ {a;b} \right]. Hỏi tổng a + b có giá trị là bao nhiêu?
Cho hàm số y = f\left( x \right) liên tục trên \mathbb{R} và có đạo hàm f'\left( x \right) = {x^2}\left( {x - 2} \right)\left( {{x^2} - 6x + m} \right) với mọi x \in \mathbb{R}. Có bao nhiêu số nguyên m thuộc đoạn \left[ { - 2019;\,2019} \right] để hàm số g\left( x \right) = f\left( {1 - x} \right) nghịch biến trên khoảng \left( { - \infty ;\, - 1} \right)?
Cho f\left( x \right) mà đồ thị hàm số y = f'\left( x \right) như hình bên. Hàm số y = f\left( {x - 1} \right) + {x^2} - 2x đồng biến trên khoảng?