Đề bài

Cho \(\widehat {AOB} = {50^0}\) và \(\widehat {BOC} = {60^0}\) sao cho \(\widehat {AOB}\) và \(\widehat {BOC}\) kề nhau. Tính số đo \(\widehat {AOC}.\)

• A. \(90^\circ \)                    
• B. \(100^\circ \)
• C. \(120^\circ \)      
• D. \(110^\circ \)

Phương pháp giải

+ Chỉ ra tia \(OB\) nằm giữa hai tia \(OA\) và \(OC\)

+ Từ đó sử dụng công thức cộng góc để tính số đo góc \(\widehat {AOC}.\)

Lời giải của GV Loigiaihay.com

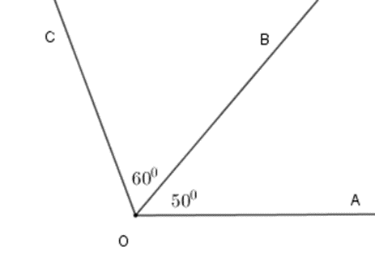
Vì \(\widehat {AOB}\) và \(\widehat {BOC}\) kề nhau nên tia \(OB\) nằm giữa hai tia \(OA\) và \(OC\)

Ta có \(\widehat {AOB} + \widehat {BOC} = \widehat {AOC} \Rightarrow \widehat {AOC} = 50^\circ  + 60^\circ \) nên \(\widehat {AOC} = 110^\circ \).

Đáp án : D