Đề bài

Tính góc \(yOz\) trên hình vẽ sau

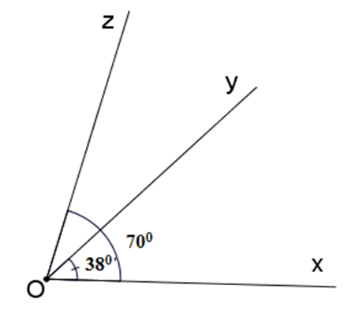
• A. \({32^0}\)
• B. \({70^0}\)    
• C. \({38^0}\)                         
• D. \({60^0}\)

Phương pháp giải

+ Chứng minh tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz\)

+ Sử dụng công thức cộng góc: Nếu tia \(Oy\)  nằm giữa hai tia \(Ox\)  và \(Oz\)  thì \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\)

Lời giải của GV Loigiaihay.com

Vì hai tia \(Oy;Oz\) cùng thuộc nửa mặt phẳng bờ là đường thẳng chứa tia \(Ox.\)

Lại có \(\widehat {xOy} < \widehat {xOz}\,\left( {38^\circ  < 70^\circ } \right)\) nên tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz.\)

Do đó \(\widehat {xOy} + \widehat {yOz} = \widehat {xOz}\) hay \(\widehat {yOz} = \widehat {xOz} - \widehat {xOy} = 70^\circ  - 38^\circ \)\( = 32^\circ .\)

Vậy \(\widehat {yOz} = 32^\circ .\)

Đáp án : A