Đề bài

Gọi \(O\) là giao điểm của ba đường thẳng \(xy;zt;uv\). Kể tên các góc bẹt đỉnh \(O.\)

• A. \(\widehat {xOu};\,\widehat {uOt};\,\widehat {tOx}\) 
• B. \(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\)        
• C. \(\widehat {xOy};\,\widehat {uOv}\)      
• D. \(\,\widehat {uOv};\,\widehat {zOt}\)

Phương pháp giải

Xác định các tia phân biệt đối nhau từ đó kể tên các góc bẹt.

Lời giải của GV Loigiaihay.com

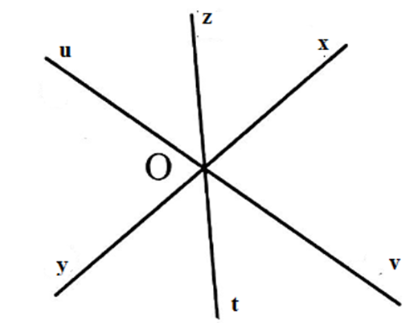
Các tia \(Ox\) và \(Oy;\) \(Oz\) và \(Ot;Ou\) và \(Ov\) là hai tia đối nhau nên các góc bẹt có đỉnh \(O\)  tạo thành là

\(\widehat {xOy};\,\widehat {uOv};\,\widehat {zOt}\) .

Đáp án : B