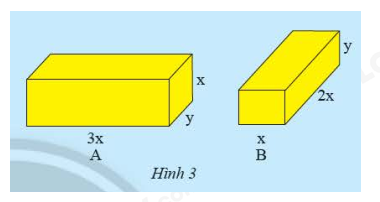
Cho hai hình hộp chữ nhật A và B có các kích thước như hình 3.
a) Tính tổng thể tích của hình hộp chữ nhật A và B.
b) Viết biểu thức biểu diễn sự chênh lệch thể tích của A và B.
Thể tích hình hộp chữ nhật là lượng không gian mà hình chiếm, được tính bằng tích của diện tích đáy và chiều cao: \(V = a.b.h\), trong đó \(a\), \(b\), \(h\), \(V\) lần lượt là chiều dài, chiều rộng, chiều cao và thể tích của hình hộp chữ nhật.
a) Thể tích của hình hộp chữ nhật A là: \({V_A} = 3x.y.x = 3.{x^2}y\)
Thể tích của hình hộp chữ nhật B là: \({V_B} = 2x.x.y = 2{x^2}y\)
Tổng thể tích của hình hộp chữ nhật A và B là: \(3{x^2}y + 2{x^2}y = \left( {3 + 2} \right).{x^2}y = 5{x^2}y\)
b) Biểu thức biểu diễn sự chênh lệch thể tích của A và B là: \(3{x^2}y - 2{x^2}y = \left( {3 - 2} \right).{x^2}y = {x^2}y\)

Các bài tập cùng chuyên đề
Bài 1 :
Xác định hằng số \(a\) để các đơn thức \({ax}{y^3}{,^{}} - 4{x}{y^3}{,^{}}7x{y^3}\)có tổng bằng \(6x{y^3}\).
-
A.
a = 9.
-
B.
a = 1.
-
C.
a = 3.
-
D.
a = 2.
Bài 2 :
Cho đơn thức một biến \(M = 3{x^2}\). Hãy viết ba đơn thức biến \(x\), cùng bậc với M rồi so sánh phần biến của các đơn thức đó.
Bài 3 :
Xét ba đơn thức \(A = 2{x^2}{y^3},B = - \dfrac{1}{2}{x^2}{y^3}\) và \(C = {x^3}{y^2}\).
So sánh:
a) Bậc của ba đơn thức A,B và C.
b) Phần biến của ba đơn thức A,B và C.
Bài 4 :
Cho các đơn thức:
\(\dfrac{5}{3}{x^2}y; - x{y^2};0,5{x^4}; - 2x{y^2};2,75{x^4}; - \dfrac{1}{4}{x^2}y;3x{y^2}.\)
Hãy sắp xếp các đơn thức đã cho thành từng nhóm, sao cho tất cả các đơn thức đồng dạng thì thuộc cùng một nhóm.
Bài 5 :
Ta đã biết nếu hai đơn thức một biến có cùng biến và có cùng bậc thì đồng dạng với nhau. Hỏi điều đó có còn đúng không đối với hai đơn thức hai biến (nhiều hơn một biến)?
Bài 6 :
Quan sát ví dụ sau:
\(2,{5.3^2}{.5^3} + 8,{5.3^2}{.5^3} = \left( {2,5 + 8,5} \right){.3^2}{.5^3} = {11.3^2}{.5^3}.\)
Trong ví dụ này, ta đã vận dụng tính chất gì của phép nhân để thu gọn tổng ban đầu?
Bài 7 :
Cho hai đơn thức đồng dạng \(M = 2,5{x^2}{y^3}\) và \(P = 8,5{x^2}{y^3}\). Tương tự HĐ5, hãy:
a) Thu gọn tổng M+P.
b) Thu gọn hiệu M-P.
Bài 8 :
Cho các đơn thức \( - {x^3}y;4{x^3}y\) và \( - 2{x^3}y.\)
a) Tính tổng S của ba đơn thức đó.
b) Tính giá trị của tổng S tại \(x = 2;y = - 3.\)
Bài 9 :
Trở lại các lập luận của Tròn và Vuông trong tình huống mở đầu. Hãy trả lời và giải thích rõ tại sao.
Bài 10 :
Sắp xếp các đơn thức sau thành từng nhóm, mỗi nhóm chứa tất cả các đơn thức đồng dạng với nhau:
\(3{x^3}{y^2}; - 0,2{x^2}{y^3};7{x^3}{y^2}; - 4y;\dfrac{3}{4}{x^2}{y^3};y\sqrt 2 .\)
Bài 11 :
Rút gọn rồi tính giá trị của mỗi đơn thức sau:
\(S = \dfrac{1}{2}{x^2}{y^5} - \dfrac{5}{2}{x^2}{y^5}\) khi \(x = - 2;y = 1.\)
Bài 12 :
Tính tổng của bốn đơn thức:
\(2{x^2}{y^3}; - \dfrac{3}{5}{x^2}{y^3}; - 14{x^2}{y^3};\dfrac{8}{5}{x^2}{y^3}.\)
Bài 13 :
Một mảnh đất có dạng như phần được tô màu xanh trong hình bên cùng với các kích thước được ghi trên đó. Hãy tìm đơn thức (thu gọn) với hai biến \(x\) và \(y\) biểu thị diện tích của mảnh đất đã cho bằng hai cách:
Cách 1: Tính tổng diện tích của hai hình chữ nhật ABCD và EFGC.
Cách 2: Lấy diện tích của hình chữ nhật HFGD trừ đi diện tích của hình chữ nhật HEBA.
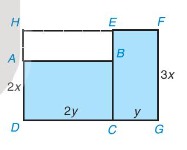
Bài 14 :
Mỗi cặp đơn thức sau có đồng dạng không? Nếu có, hãy tìm tổng và hiệu của chúng.
a) \(xy\) và \( - 6xy\)
b) \(2xy\) và \(x{y^2}\)
c) \( - 4yz{x^2}\) và \(4{x^2}yz\)
Bài 15 :
Đơn thức nào sau đây đồng dạng với đơn thức \( - 2{x^3}y\)?
A. \(\dfrac{1}{3}{x^2}yx\)
B. \(2{x^3}yz\)
C. \( - 2{x^3}z\)
D. \(3x{y^3}\)
Bài 16 :
Các đơn thức trong mỗi trường hợp sau có đồng dạng hay không? Vì sao?
a) \({x^2}{y^4}; - 3{{\rm{x}}^2}{y^4}\) và \(\sqrt 5 {x^2}{y^4}\)
b) \( - {x^2}{y^2}{z^2}\) và \( - 2{{\rm{x}}^2}{y^2}{z^3}\)
Bài 17 :
a) Tính tổng: \(5{{\rm{x}}^3} + 8{{\rm{x}}^3}\)
b) Tính hiệu \(10y^7 - 15y^7\)
Bài 18 :
Thực hiện các phép tính:
\(a)4{{\rm{x}}^4}{y^6} + 2{{\rm{x}}^4}{y^6}\)
\(b)3{{\rm{x}}^3}{y^5} - 5{{\rm{x}}^3}{y^5}\)
Bài 19 :
Các đơn thức trong mỗi trường hợp sau có đồng dạng hay không? Vì sao?
a) \({x^3}{y^5}; - \dfrac{1}{6}{x^3}{y^5}\) và \(\sqrt 3 {x^3}{y^5}\)
b) \({x^2}{y^3}\) và \({x^2}{y^7}\)
Bài 20 :
Thực hiện phép tính:
a) \(9{{\rm{x}}^3}{y^6} + 4{{\rm{x}}^3}{y^6} + 7{{\rm{x}}^3}{y^6}\)
b) \(9{{\rm{x}}^5}{y^6} - 14{{\rm{x}}^5}{y^6} + 5{{\rm{x}}^5}{y^6}\)
Bài 21 :
Cho đơn thức \(15{x^3}{y^2}z\)
a) Hãy viết bốn đơn thức có phần hệ số khác 0 và cùng phần biến của đơn thức đã cho.
b) Hãy viết ba đơn thức có phần biến khác phần biến của đơn thức đã cho.
Bài 22 :
Tìm các cặp đơn thức đồng dạng trong các đơn thức sau:
\(2{x^2}yz\); \( - 6x{y^2}\); \({x^2}y\); \(7{x^2}yz\); \(4x{y^2}\); \( - 8xyz\)
Bài 23 :
Dựa vào tính chất phân phối của phép nhân đối với phép cộng các số, hãy thực hiện các phép tính sau và viết kết quả dưới dạng đơn thức thu gọn.
a) \(2{x^2}y + 7{x^2}y\);
b) \(6x{y^3} - 9x{y^3}\).
Bài 24 :
Tìm tổng và hiệu của hai đơn thức \(6{x^3}y\)và \(11{x^3}y\).
Bài 25 :
Tìm diện tích của phần được tô màu trong Hình 1.2 và Hình 1.3 theo \(a\)và \(b\).
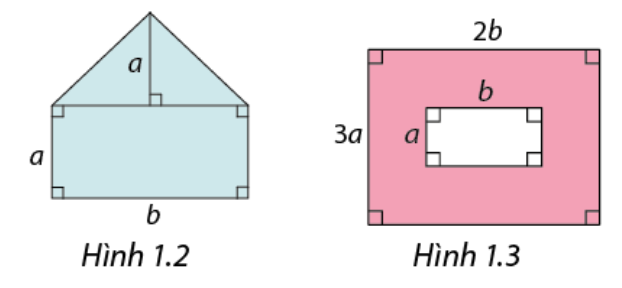
Bài 26 :
Viết hai đơn thức đồng dạng với đơn thức \( - 2x{y^2}\) rồi tính tổng và hiệu của hai đơn thức đó
Bài 27 :
Tìm tổng của các đơn thức:
\(\frac{1}{3}x{y^2}z\);\(\frac{1}{2}x{y^2}z\); \(\frac{1}{6}x{y^2}z\).
Bài 28 :
Tìm mỗi đơn thức thích hợp cho mỗi ô:

Bài 29 :
Bạn An mua \(x\) cây bút chì với giá \(y\) nghìn đồng một cây. Sau đó An mua vở với số lượng gấp đôi số bút chì đã mua. Biết giá một quyển vở gấp 5 lần giá một cây bút chì, viết biểu thức tính tổng số tiền An dung mua bút chì và vở.
Bài 30 :
Trong một hội trường có ba khu vực A, B, C. Mỗi khu vực A và C có \(a\) hàng ghế và mỗi hàng có \(b\) chiếc ghế. Khu vực B cũng có \(a\) hàng ghế nhưng mỗi hàng chỉ có \(1,5b\) chiếc ghế.
a) Viết biểu thức tính tổng số ghế của ba khu vực này.
b) Tổng số ghế của hai khu vực A và C nhiều hơn số ghế của khu vực B là bao nhiêu chiếc ghế?


















Danh sách bình luận